IIDE Proceedings 2014 ~ Cognitive Time Distortion As A Source Of Risk In Economic Organizations: Conceptual Foundations

• by: Fabian von Schéele & Darek M. Haftor

Photo: www.officemuseum.com

This paper introduces two kinds of risks present in any economic organization: the risk of cognitive time distortion and the risk of economic distortion. These two kinds of risks are related in a complex and non-linear manner, so that the cognitive distortion risk gives rise to the economic distortion risk. By monitoring the cognitive distortion risk, managers may also control the economic distortion risk. Basic conceptual foundations for the conception of these two kinds of risks, originating in unconditional human cognitive time distortion, are elaborated in this paper.

“.. if economic organization is formidably complex, which it is, and if economic agents are subject to very real cognitive limits, which they are, then failures of alignment will occur routinely.” – O.E. Williamson, 1991: 79

1. Introduction
Whether we like it or not, our lives are highly dependent upon, and conditioned by, a large number of economic organizations, such as hospitals, schools, banks, pharmaceutical companies or governmental bodies. At the same time, today’s economic organizations are exposed to a never before experienced amount of challenges of various kinds. To handle these challenges successfully, a manager’s job includes the identification and management of various organizational risks. To this end we introduce here two kinds of risks present in any economic organization, yet not previously articulated. These are the Cognitive Time Distortion Risk and its consequence, the Economic Distortion Risk.
The first-mentioned risk constitutes a source of economic inefficiencies, output quality deficiencies, and human ill-being. The second-mentioned risk articulates the economic inefficiencies. Both risks may be identified and monitored, which constitutes an opportunity for their management. This paper provides the conceptual foundation for the conception of the two kinds of risk.
The approach of the concept distortion of risk is inspired by systems theory, though this paper is focused on elaborating the operationalization of distinct mathematical metrics. In this paper, the term “risk” is applied since it has a mathematical definition in economic and psychological science based on probability theory. In systems theory however, the term “risk” is not applied or defined, but we interpret the systems theoretical concept of “variety” as being a proper connotation of ‘variance’ or ‘standard deviation’. Therefore, we will conclude this paper with a more general discussion about risk, variety and system homeostasis.
We will start with a brief recapitulation of the notion of an economic organization and some of its central characteristics pertinent for this elaboration, including the temporality of an economic organization, and then introduce the central notion of cognitive time distortion, unconditionally inherent to all human activities. This cognitive time distortion is then introduced into the conventional profit equation and further transformed into a workload equation, which results in the expression of the risk of economic distortion introduced here. A brief illustration of the model introduced here is provided followed by a discussion where we put the risk distortion concept into a systems theoretic perspective. The paper ends with some key conclusions.

2. Economic Organizations and their Temporality
Before presenting the actual mechanism that gives rise to operational and economic risks due to cognitive time distortion, we would like to provide some of its background in terms of the conception of an economic organization, its relation to time and the crucial articulation of Cognitive Time Distortion.

2.1 Economic Organizations and their Temporality
Starting with the observation that our contemporary societies are inevitably populated by a large set of social organizations of various kinds (e.g. Pfeffer, 1997), one central subset of social organization is the economic organization, as manifested by a firm, a public organization, and an NGO (e.g. Foss & Loasby, 1998). Briefly, economic organizations are understood here as those legal entities where coordinated activities are conducted by human and non-human actors, and where these activities, together with their various resources, give rise to economic incomes and costs (ibid.). Further, and central here, is that the governance of an economic organization includes formal (and informal) contracts, with both factor and product markets (ibid). In the present context we wish to articulate the distinction between two ordinary kinds of contracts: fixed-price contracts and current-account contracts, applicable to both factor and product markets, and to both goods and services. Fixed-price contracts are understood as business agreements with a predefined time-volume, price per time unit and date for delivery, while current-account contracts are understood as business agreements with only a predefined price per time unit – we will return to the two contract forms later, and now turn our attention to time.

Central to this elaboration is the fact that all kinds of social organizations, hence also the economic organization; unconditionally operate temporally simply because of their constituting actors: human beings; these experience time (e.g. von Schéele, 2001). Further, it is now well established that organizations may operate simultaneously with different kinds of time (e.g. Orlikowski & Yates, 2002; Dooyeweerd, 1955). In the present context we wish to draw attention to the fact that for a long time studies in mental and medical sciences have reported that humans operate simultaneously with physical (clock) time and cognitive (mental) time (e.g. Block & Eisler, 1999; Levin & Zackay, 1989) – unfortunately and strangely these well-documented observations have largely been ignored by economic, organization and management studies, which this contribution will attempt to remedy. The complex relation between physical time and cognitive time is addressed below.

2.2 Cognitive Time Distortion and its Nature
From our everyday experience, we know that in relation to any event such as an organizational process, project, or even a single activity, physical time measures time in terms of what the clock measures, which in turn has an established relation to a particular physical event (i.e. a second is conceived as duration of a specified amount of periods of the radiation of cesium atom in its ground state at a temperature of 0 (ISU, 1998)). On the other hand, cognitive time is what an individual human actor perceives in relation to the given event and the related clock-time measure. Cognitive time assessment made by an individual tends to move in jerks and jumps, while physical time passes smoothly and at an

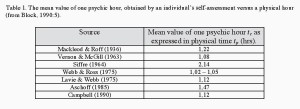
Table 1. The mean value of one psychic hour, obtained by an individual’s self-assessment versus a physical hour (from Block, 1990:5).

even pace (e.g. Levin & Zackay, 1989). For example, if a software consultant works for three and a half hours for a given client (measured in reference to a clock) however without consulting her watch, she may have perceived and also reported that she worked three hours only, meaning that half an hour has been ‘lost’. When individuals estimate time durations they nearly unconditionally, unintentionally and unknowingly, commit errors resulting in significant differences between the self-assessed cognitive time duration and the corresponding physical time duration, as measured by a clock (ibid.). A review of current research within cognitive time distortion suggests that the gap in correct assessment of one hour may vary between 1,02 – 2,14 hours, see Table 1 for an overview.

In general terms, cognitive time distortion (CTD) is understood here as being the ratio between cognitive time (t_c) and physical, or clock, time (t_p). In appraising time distortion, it is necessary that cognitive and physical time have the same frame of reference, and that they address the same event – e.g. an activity, a process, a project, or a service contract. Therefore, and more specifically, time distortion, denoted here with “τ_i”, is defined as the ratio between cognitive time, t_c, and physical time, t_p, of a certain event “i”, hence formally:

One central implication from the empirical studies conducted is that CTD is unconditional to human nature (Aschoff, 1985); hence it is not a question of whether we commit a CTD or not, it is a question of how much distortion is produced.

2.2.1 The Probabilistic Nature of Cognitive Time Distortion
Cognitive time distortion exhibits a stochastic pattern, varying serendipitously during any one day. Empirical investigations show that CTD has a stochastic pattern both at the level of an individual subject and at the level of a group of subjects; however the deviations are more pronounced when, for example, a service is performed by a group of individuals than by an individual actor, hence at the group level (von Schéele, 2001) – see Figure 1.

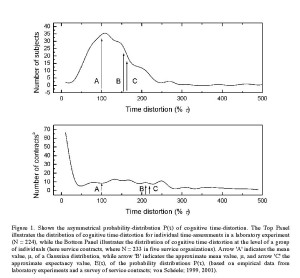
Figure 1. Shows the asymmetrical probability-distribution P(τ) of cognitive time-distortion. The Top Panel illustrates the distribution of cognitive time-distortion for individual time-assessments in a laboratory experiment (N = 224), while the Bottom Panel illustrates the distribution of cognitive time-distortion at the level of a group of individuals (here service contracts, where N = 233 in five service organizations). Arrow ‘A’ indicates the mean value, μ, of a Gaussian distribution, while arrow ‘B’ indicates the approximate mean value, μ, and arrow ‘C’ the approximate expectancy value, E(τ), of the probability distributions P(τ), (based on empirical data from laboratory experiments and a survey of service contracts; von Schéele; 1999, 2001).

2.2.2 The Statistic and Asymmetric Nature of Cognitive Time Distortion
To further elucidate the statistical nature of the time distortion τ, consider P(τ) as being the probability function of the stochastic time distortion variable τ. Let also p(τ) express the probability that a time distortion of magnitude τ occurs. The expectancy value E(τ) of the time distortion τ in a set consisting of “i” events, [i = 1…r], can then be defined as E(τ) = Σ p(τ _i) τ _i. Provided that the individuals of a given population are unbiased or randomly biased, the time distortion will then exhibit a probability distribution P(τ) with the following properties:
i. P(τ) is not symmetrically distributed around τ = 1, which implies that the arithmetical mean value μ_τ ¹ 1 and the expectancy value E(τ) ¹ There exist several empirical evidences supporting this, showing that individuals assessing time exhibit a tendency to overestimate the passage of time (e.g. Aschoff, 1985; von Schéele, 2001).
ii. P(τ)  is not Gaussian-distributed, but exhibits instead an asymmetric distribution with a long “tail” for values of τ > 1 (von Schéele & Haftor, 2013). In such distributions it should not be expected that the arithmetical mean value μ_τ corresponds to the expectancy value E(τ). Serious errors will be committed if a Gaussian distribution of time distortion is assumed in economic calculus, as such an assumption, in turn, builds on presuppositions that both the arithmetical mean value μ_τ and the expectancy value E(τ) are equal to unity.

To illustrate this point, an investigation of five service organizations (von Schéele, 2001) showed that the arithmetical mean value μ_τ and the expectancy value E(τ) of P(τ) were greater than 2. Thus, the time estimations of the employees exceeded the actual contracted time, indicating a general overestimation of the passage of time. Furthermore, only 16% of the customers received a service-time that matched contractual time. The practical consequences of this were large deviations from budgeted economic outcome as well as poor profitability of the investigated service operations, ultimately resulting in the need to discharge employees (see von Schéele (2001) for further details).

3. The Dissimilar Effects of Cognitive Time Distortion due to Contractual Form
We would like to recall a central operating assumption of this elaboration: that an economic organization is made up of purposeful conduct by humans, whatever kind it may be, and of contracts between, on the one hand, the client or customer and the organization, and on the other hand, between the employee and the organization (e.g. Coase, 1937).

Given these assumptions, cognitive time distortion may cause an economic distortion in the manufacturing of products, in two alternative ways, both related to the nature of the contract between the supplier and the customer, and are specifically linked to the irreversible property of time. In general, the two different economic agreements applied on the market are:
i. Service delivery at a fixed price (fixed-price contract). The service provider and the customer have agreed upon the time-volume of the service (t_p), the price, and the date of delivery, after which the service delivery starts. The service delivery ends when the predefined service has been executed. The time distortion τ (alternatively δ) is considered here with reference to the predefined time t_p (alternatively predefined target capacity e_p) in the fixed price contract.

ii. Service delivery at current account. The service provider and the customer have agreed upon the price per time-unit for the service. The total time-volume (t_p), however, remains unspecified. This implies that the service also remains unspecified. For each additional performed hour of the service delivery, the service provider will charge the customer. For this economic agreement the time distortion τ is considered with reference to physical clock time (t_p).

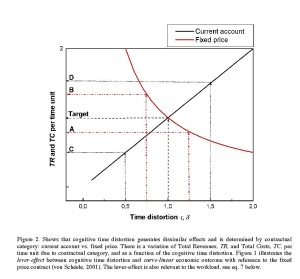
Figure 2. Shows that cognitive time distortion generates dissimilar effects and is determined by contractual category: current account vs. fixed price. There is a variation of Total Revenues, TR, and Total Costs, TC, per time unit due to contractual category, and as a function of the cognitive time distortion. Figure 1 illustrates the lever-effect between cognitive time distortion and curve-linear economic outcome with reference to the fixed price contract (von Schéele, 2001). The lever-effect is also relevant to the workload, see eq. 7 below.

The total revenues per time unit (income; TR), and the total costs per time unit (TC), are both influenced, however differently, by cognitive time distortion through the two distinct contractual means in Figure 2, as discussed below.

First, consider the fixed-price contract. If employees overestimate the time-volume delivered, resulting in cognitive time, t_c, exceeding contracted or physical time, t_p, the time distortion, τ will be larger than unity, thus decreasing TR per time unit (A in Figure 1). On the other hand, an underestimation of the time delivered affords a time distortion, τ, less than unity, and TR will increase (B in Figure 1). Thus, from this we are able to draw the conclusion that time distortion, τ, is inversely proportional to TR for the fixed-price contractual model.
Secondly, consider now the current account contract. Here, the customer is charged for the contractor’s cognitive time assessment, t_c, regardless of whether it equals the actual clock, i.e. physical, time delivered, t_p, or not. Underestimation of the passage of time – leading to undercharging – causes a decrease in TR (C in Figure 1) and the time, t_c, reported to the customer will be less than the actual time delivered, t_p. The opposite will occur if time is overestimated (D in Figure 1). Therefore, the influence of time distortion, τ, on TR is linear for contracts on current account (von Schéele, 2001).

Before moving on to elaborate the consequences of these dissimilar effects of cognitive time distortion due to contractual form, we wish to make a brief observation. The key role of the mode of a commercial contract in relation to production time and for economic results of an organization, as we understand it, appears so far to have passed unnoticed in economic studies. Subsequently, the relation between cognitive time leakage and the economic outcome has traditionally been assumed to be linear.

4. Cognitive Time Distortion, Contracts and Risk
We can conclude now that the emergence of cognitive time distortion is an unconditional state of human affairs, both at the level of a single human and at the level of a group of humans. We also know that CTD is not symmetrically or normally distributed, which implies that there are no simple means for ignoring it. Next, CDT has a dissimilar effect on an economic organization due to the contract form assumed. Indeed, in a previous elaboration where CTD was embedded into the traditional profit equation, we showed that CTD may have a non-linear and somewhat dramatic impact on costs, revenues and thus profits of a firm (von Schéele & Haftor, 2014). It is also argued there that CDT has a negative impact on economic productivity, output quality and human worker well-being (ibid.).
As CDT emerges both in prospective (e.g. budgeting) and retrospective (e.g. reporting) worker assessments (e.g. von Schéele, 2001), and as formal contracts are bound to physical time only, i.e. do not account for cognitive time, CDT gives rise to an undesired behavior in the economic organization, when the latter deviates from the ideal of a perfect contract where no difference between the physical time and the cognitive time is present.
On the other hand, as CTD can be estimated empirically, both at the level of an individual and the level of a group of individuals, a probability distribution may be identified and constitute the source of risk assessment and management. For example, if measurements show that a given economic organization manifests a CTD of 1,12, this shows that each individual leaks on average 12% of its time, where time leakage may be understood here as an individual human worker consuming 12% time more than accounted for by the formal contracts. We denote this kind of risk here as “CDT-risk” (alternatively as first order risk). The key question here is what magnitude of CTD is present in a given economic organization (rather than if it is present). While this first order risk can be measured and identified quite straightforwardly, we also wish to introduce here another kind of risk that is related to the first order risk yet hidden in the economic set-up of an economic organization. We denote it here as “CTD-economic risk”, alternatively as second order risk. We will show later that this second order risk is related in a complex manner to the first order risk, and indeed caused by CTD-risk, and that it has important implications on the performance of an economic organization.

5. The Second Order Risk: CTD’s Economic Risk
We will start the elaboration of the second order risk with the conventional notion of profit, as expressed in the following equation:

In Eq. 2, π signifies here profit per time unit, TR the total revenues per time unit, and TC the total costs per time unit. The parameters are expressed in monetary units (U), preferably defined for the time unit of one year. It is useful to consider the total workload-time to customers, t_vol, of an economic organization on a yearly basis, while the market price for each hour delivered, p, is considered on an hourly basis. Accordingly, the expression TR = p t_vol denotes the total annual revenues of one economic organization, here a service provider, that charges its customer the price of p U/hour, for the total workload time-volume of t_vol hours in a year. The employee salary per time unit is related to the market price, p, by the weight v_p, where [0 < v_p < 1], so that the salary cost per time unit of one employee becomes v_p p. Thus, we can write eq. 1 as follows:

The expression between the parenthesis in Eq. 3 is the expression that will be further elaborated into the distortion economic function Q(τ). Firstly, consider a modification of Eq. 3 to express total workload-time to customers:

From Eq. 4 follows, that the more approaches 1, the higher the workload becomes, as measured in hours. Since CTD affects economy differently, depending on mode of contract, the variable α, [0 £ α £ 1] is used, where a value of unity signifies 100% of fixed-price contracts (and a value of zero signifies contracts on current account). In the following equation, it is assumed that the TR may consist of a mix of fixed price contract and a contract on current account.

Now we insert the CTD-variable t from Eq. 1 to Eq. 4, paying attention to the linear or inverse effects of CTD due to contractual category (von Schéele, 2001; von Schéele & Haftor 2014). Observe that the fixed price contracts are multiplied by (or ), as discussed in Figure 1 above, while contracts on current account are simply multiplied with . In addition, CTD on Total Costs is here denoted by the symbol. For an organization with one customer contract (partly fixed price and partly on current account) and one employee, the workload is consequently as follows:

Eq. 6 exhibits time distortion in workload, as expressed in the case of one customer contract and one employee contract. Should the economy consist of several customers and employees, eq. 6 becomes more elaborate, with summation signs for “i” customer contracts and “j” employee contracts. This, however, lies outside the scope of this paper. We have now arrived at an equation in the following form:

Eq. 7 articulates that the total workload is dependent on τ and δ, and that the distortion function, , has an inverted influence on the total workload. Eq. 7 expresses the workload-time to customers, and signifies that the physical time values are dependent upon two kinds of risks:
i) The first order risk, here mathematically defined by P(τ) alternatively P(δ), which is an expression of the concept of CTD. This risk expresses the probability that a time distortion of magnitude τ (alternatively δ) will occur.
ii) The second order risk, here mathematically defined by the distortion function P(1/Q(τ)), which expresses the probability that an error of magnitude 1/Q(τ) will occur. This economic risk spells out the lever effect between the CTD and specifically the workload of an organization.

To demonstrate the relation between the first order risk and the second order risk – the lever effect – we consider a CTD with a magnitude of τ = 1,1, which means that each subjective hour is 10% longer than the physical hour. In addition, we assume a service delivery on a fixed price contract ( = 1) and the market price margin corresponding to 0,6 (which means that salary level per hour is 60 % of market price per hour). A value of τ exceeding 1 automatically makes δ fall below the value of 1, so we insert δ = 0,9.

Consider first Eq. 6 without any CTD:

This shows that a workload of 2,5 times profit per market price corresponds to the budgeted time under present conditions.

Consider now Eq. 6 with CTD of 1,1:

This represents an augmentation of 67 %. We can spell it out more formally by writing:
τ = 1,1 → 1/Q(1,1) = 1,67 under present conditions; (the arrows symbolizes ‘bring about’).

This is the so called ‘lever-effect’. It cannot be argued that first order risks, P(τ), occur with the same probability as second order risks, P(1/Q(τ)). We do not have any support that there is any linear correlation between the first order risk (CTD) and the second order risk (economy). However, due to the lever effect, there is a mathematical-statistical support that the standard deviation of 1/Q(τ) exceeds that of τ.

Indeed, Figure 1 above shows that the asymmetrical probability function P(τ) of CTD differs, depending on whether the CTD originates from a laboratory setting or a business setting. In a business setting, the compounded time distortion τ exhibits a larger standard deviation, and there is a lower probability that it corresponds to unity (100 %), compared to laboratory settings. One explanation of this phenomenon is that any compounded time distortion forms an addition of the stochastic variables τ_a and τ_b, and addition of stochastic variables also induces an addition of their mean values as well as their standard deviations. Thus, compounded time distortion, such as for instance the aggregated time records of employees in a project, always has a larger variance than that of a single individual.

With these facts in mind, we can therefore make the following proposition:
CTD Risk Proposition: The CTD risk on the first level in a system always gives rise to greater risks in interrelated second order systems.

Therefore, with due respect to the perilous mechanism between CTD and the distortion function, we need to investigate how to control Q(τ), by means of controlling τ. This however lies outside the scope of this paper.

6. Discussion
In a systems science perspective, this paper addresses several different kinds of systems. According to the General Living Systems Theory (GLS, Miller; 1978), the variation dealt with here occurs within and between the Organism, the Group and the Organization. While Miller points out that each of these living systems include many non-living components or artefacts, that are crucial for the living system, we argue that some of the artefacts (economic formulas) are erroneous or wrong and misinterpret the environment in which the living system is trying to survive. Our suggestion is subsequently, that living systems with erroneous artefacts are endangered.
Miller argues that each level in the GLS is dependent on 20 subsystems to be able to support the phenomenon of life. For instance, subsystem “Input transducer” (no 11), “Internal transducer” (no 12), “Timer” (no 14), “Decoder” (no 15), “Encoder” (no 19) and “Output transducer” (no 20) may be relevant for the future research of CTD. At the present, however, we have treated them as a black box, mainly focusing on the variation between the different levels of living systems; the Organism, the Group and the Organization. There does exist one important difference in our approach compared that discussed by Miller; we stress that the variation – the CTD – occurs without the living systems being aware of it. Regardless of whether it is an organism, a group or an organization, the CTD is an unapprehensive variety.

The Viable System Model (VSM, Beer, 1972) suggests a recursive model comprising of 5 different managerial subsystems. To handle the organization, the manager has to tame the mess according to some principles of the model, where the main concern is the control function and the concept of variety. The word “control function” should not be interpreted mathematically, since Beer does not suggest any particular mathematical approach. Instead, he focuses on the structure of the management system and defines the roles of each subsystem. In his VSM, Beer pronounces the importance of the terms variety, comparator, oscillation, attenuator, amplifier and transducer, to mention a few. However, little is said about operationalization of the terms with reference to individuals and economy. To this end, we present an operationalization of the variety (time-based variety) which may support measurement of amplification, transduction, oscillation and attenuation in systems as well.

Finally, the account for two kinds of temporal experience as offered here – the mechanical and the cognitive, echoes the antireductionist signals suggesting that humans operate with several kinds of temporal experiences, where the late Dutch philosopher Herman Dooyeweerd (1894-1977) proposed fifteen modalities of human experience, hence fifteen kinds of temporal experience, such as physical, biological, historic, economic, cognitive, social, and moral (Dooyeweerd, 1955). One of his key messages was not to reduce one kind of experience – here concerning time – to another one. In this sense, we offer one small step toward such an agenda, where we formalize two kinds of temporal experiences – the physical and the cognitive – and we also offer a formal relationship between the two, and a link between the described relation and the economic implications of an organization. In that manner our contribution validates Dooyeweerd’s argument of multiple temporal experiences, and probably also extends it somewhat by showing that the various modalities may manifest non-trivial intermodal relationships, due to the latter’s non-linear character.

7. Conclusions
In this paper we have presented two kinds of risks present in any economic organization, namely:
The first order risk, understood as the magnitude of Cognitive Time Distortion, or the probability that the human cognitive system conceives a time assessment of level τ (or δ).
The second order risk, understood as the probability that the distortion function, here defined by 1/Q(τ,δ), assumes a given value with respect to budgeted economic targets.

The two kinds of interrelated risks introduced here, present in any economic organizations, stem from the inevitable human fallacy of time assessment. In this, the second order risk may be conceived as a lever effect of the first order risk, implying that the second order risk may be controlled when the first order risk is monitored and influenced. This, in turn, suggests that there is a need to identify practical means for identifying and influencing cognitive time distortion in economic organizations, with the potential benefit of improving their economic productivity, output quality, and peoples’ well-being.

NOTES
[i] Fabian von Schéele – Corresponding author: fabian.vonscheele@lnu.se; Linnaeus University, Växjö, Sweden
[ii] Darek M. Haftor – Linnaeus University, Växjö, Sweden

REFERENCES
Ashoff, J. (1985). On the perception of time during prolonged temporal isolation, Human Neurobiology, 4, pp.41 – 52.
Beer, S. (1972). The Brain and the Firm, Penguin Press, London.
Block, R.A., Eisler, H. (1999). The complete bibliography on the psychology of time, 1839 –1999. [Machine readable data file]. Bozeman: Montana State University, Department of Psychology [Producer and Distributor].
Campbell, S. S. (1990). Circadian Rhythm and Human Temporal Experience. In R. A. Block (Ed.) Cognitive Models of Psychological Time, Lawrence Earlbaum Ass. pp. 101–118.
Coase, R.H. (1937). The nature of the firm. Economica, N.S., 4 (16), 386-405.
Dooyeweerd, H. (1955). A New Critique of Theoretical Thought, Edwin Mellen.
Foss, N.J., Loasby, B.J. (1998). Economic Organization, Capabilities and Co-ordination. Essays in Honour of G.B. Richardson. Routledge, London.
ISU (1998). Organisation Intergouvernementale de la Convention du Métre, 1998. The International System of Units (SI), 7th Edition (PDF). Retrieved 2011-04-09.
Levin, I., Zackay, D. (Eds.) (1989). Time and Human Cognition. North-Holland: Elsevier Science Publishers.
Macleod, R., B., Roff, M.F. (1936). An experiment in temporal disorientation. Acta Psychologica, Vol. 1, pp.381–423
Miller, J. (1978). Living Systems, McGraw-Hill, NY.
Orlikowski, W. J., Yates, JA., (2002). It’s about time: temporal structuring in organizations. Organization Science, Vol. 13, No. 6, pp. 684–700.
Pfeffer, J. (1997). New Directions for Organization Theory. Problems and Prospects. Oxford University Press, Oxford
Siffre, M. (1964). Beyond time. New York: McGraw-Hill.
Vernon J.A., Mcgill T.E. (1963). Time estimations during sensory deprivation. J Gen Psychol. Jul; 69:11-8.
Von Schéele, F. (1999). Business Risks in Service Companies due to Poor Temporal Assessment. In: B. Green (Ed.) Risk Behavior and Risk Management in Business Life. Kluwer Academic Publishers.
Von Schéele, F. (2001). Controlling Time and Communication in Service Economy. Doctoral Thesis. Royal Institute of Technology, Stockholm.
Von Schéele, F., Haftor, D.M. (2014). Cognitive Time Distortion on the Performance of Economic. Systems Research and Behavioral Science, Vol. 31, No.1, pp. 77-93.
Williamson, O.E. (1991) Strategizing, Economizing, and Economic Organization. Strategic Management Journal, Vol. 12, 75-9

You May Also Like

The International Institute For Development And Ethics

IIDE Proceedings 2014 ~ Introduction: Social Change In Our Technology-Based World

IIDE Proceedings 2014 - A Transcendental Inquiry Into ‘Academic Capitalism In The New Economy’

IIDE Proceedings 2014 - Corporate Social Responsibility, Deconstruction And Justice: A Response To Campbell Jones And Richard T. De George

IIDE Proceedings 2014 ~ The Cultural Basis For A Sustainable Community In A South African Township

IIDE Proceedings 2014 - The Informal Sector And Local Economic Developments In South Africa: An Evaluation Of Some Critical Factors

Comments