ISSA Proceedings 2002 – Using Argument Types

• by: John Hoaglund - Center for Critical Thinking, Christopher Newport University

1. Introduction
In North America, serious students of natural-language argument are familiar with the four basic argument types given wide currency in the work of Stephen N. Thomas(1997): convergent, linked, serial, and divergent. Yet it is possible that these types are more discussed as theoretical possibilities than actually applied in the analysis and evaluation of arguments in natural language. Here I consider briefly two problems that may hinder such wider application. There is uncertainty over the role these types should play in our work with arguments, and in particular over what (if anything) remains to be done once an argument has been found to be of a certain type. These argument types will also be briefly compared with those of the Amsterdam School, and then also with the argument forms of formal logics.
The other factor that may currently limit application is that few arguments of interest to us fit a basic type. Such arguments are too complex. So the question is whether the typology can be extended to accommodate more complex arguments. What I say about these large questions in brief compass cannot hope to be more than suggestive, but my goal is to diminish barriers to the wider application of these types in the analysis and evaluation of arguments in natural language.
Arguments in natural language are claims backed up with evidence or reasons. They are found almost anywhere language is used, but especially where someone is trying to convince us that a claim is true. So virtually any print medium can present arguments, e.g. a website, but editorials in periodicals, material on op-ed pages in newspapers, or articles or books written to support a position or theory are particularly good sources. Debates in academe, indeed discussions of papers at conferences like this one, or exchanges like those on the TV program Crossfire are rich with oral arguments.
This argument typology developed from the use of arrow diagrams to portray relations of (claimed) logical support in arguments in print media. Whenever it is obvious what the argument is, and that the argument is strong or weak, diagraming isn’t needed. Diagraming and the argument types developed in the work of Monroe Beardsley(1975) and Thomas(1997) are here regarded as analytical tools, crafted to help us understand and evaluate arguments that need explaining or interpreting, or arguments so important that we must be especially careful in evaluating them. I will here refer to those informal logicians who work with arrow diagraming and the Thomas typology as argument analysts or analysts for short (Hoaglund 1999).

2. Role of the Types
It is useful to distinguish identifying, analyzing, and evaluating an argument. To identify an argument is to recognize a claim backed up with reasons or evidence. To analyze it is to understand how the premises are intended to support the conclusion. To evaluate it is to decide whether it is weak or strong, whether the premises actually support the conclusion. Working with an argument is often a process of trial and error with some backtracking, and identifying can shade into analysis, and the latter be affected by evaluative concerns. But deciding whether a specific statement is advanced as a premise belongs to identifying the argument, although it may involve some analysis. Determining whether all premises directly support the conclusion or whether the argument has one or more intermediate conclusions is part of analysis. Judging whether a premise is sufficiently reliable to provide considerable support for the conclusion pertains to evaluation.
Argument diagraming and types fall clearly into the analysis area of our work with arguments in natural language. Distinguishing a convergent argument from a linked will illustrate. Kate Phillips provided the following convergent argument (www.bloomington) about a position on procedures taken by the American Veterinary Medical Association.

Here each premise provides separate, independent support for the conclusion. Suppose that by using anaesthesia and providing outstanding post-op care ? is made to yield little or no support for ?. The argument could still be strong based on the support of ? and ?. Support in the convergent argument is cumulative, the sum total of what ? plus ? plus ? contribute. In this latter feature – cumulative support – the convergent argument is similar to coordinatively compound argumentation of the Amsterdam School.

We can contrast this with the following linked argument about the Muslim fundamentalists who formerly ruled Afghanistan (New Republic 2000, 42).

In the linked argument the premises depend on each other – they must work together to provide possible support for the conclusion. Here, as Ralph Johnson pointed out(i), the conclusion makes a bold claim. ? by itself offers almost no support for it. Male doctors not treating women might support a claim “ill-advised” or “odd’ but not “insane.” Joined with ?, however, there is a “leap of support” (Yanal’s [1984] phrase) that can yield a strong argument. To my knowledge, no argument type of the Amsterdam School corresponds to the linked argument in this respect. But we 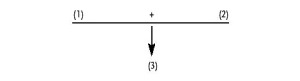have no space to further pursue the distinction of linked and convergent argument here (Hoaglund 2000).

What remains to be done when we have identified the type of an argument? Determining the type on the basis of an arrow diagram concludes the analysis phase of our work with the argument. What remains is evaluation, deciding whether the argument is weak or strong. Analysis prepares the way for evaluation – otherwise there is no point in doing it. But it is not itself evaluation. The premises must be checked for reliability and relevance to the conclusion. Both above arguments pass this test. The modality of the conclusion must be assessed – how much does it claim relative to the evidence? We have already commented on the bold claim of the linked argument and the strength of support needed to sustain it. The conclusion of the convergent makes a comparatively modest claim, which contributes to the strength of the argument. “Vets should counsel” is much more modest than e.g. “Vets should not perform these surgeries.” But to assess the convergent argument with the above premises and this conclusion we do need to consult the dialectical tier (Johnson 2000, 164-174 et passim), the larger controversy or debate of which it is a part. What reasons do dog owners have for desiring such surgeries on their pets? Balancing these reasons against those cited in the premises would allow a more accurate estimate of the argument’s strength.

The four basic argument types are descriptive of ways people argue over matters of substance in natural language. They sum up and communicate information from arrow diagrams that can be useful in assessing the strength of arguments. But assessing strength goes beyond diagram and argument type to consider such factors as context, premise reliability and relevance, and modality of the conclusion.

I would add one argument type to the basic four of Thomas (the Thomas types): the simple argument, one premise supporting a conclusion. It is a distinct type rather than the basic unit of all arguments, the role of the otherwise similar single argumentation of the Amsterdam School (Eemeren & Grootendorst 1984, 90-93). We communicate more efficiently when we refer to the simple argument rather than to the argument with one premise supporting a conclusion, much as we now say “convergent argument” rather than “argument with two or more independent premises converging on a conclusion.”

3. Types in Pragma-Dialectics and in Formal Logics
Further clarification of the role of these types in the analysis and evaluation of arguments in natural language may be won by contrasting them with the diagram types of the pragma-dialecticians of the Amsterdam School and with the argument forms of formal logics. Freeman’s excellent study (Freeman 1999) is the starting point for any comparison of argument types between informal logicians and pragma-dialecticians.

The pragma-dialecticians are also focused on argument in natural language, and their diagrams resemble ours. The diagram for coordinatively compound argumentation resembles that of the linked of the informal logicians with the arrow pointing up instead of down, and, similarly inverted, that for multiple argumentation resembles the convergent. These resemblances are quite deceptive, however. Argument analysts – informal logicians who use arrow diagrams and the Thomas types – treat an argument as a unit with a more or less complex structure of premises comprising basic support statements and intermediate conclusions, the whole being defined by the final conclusion, the point the writer or speaker is trying to prove. We tend to speak of support relations in an argument. Our goal can be stated as that of the critical thinker: we want to determine whether the conclusion receives sufficient support to be added to our store of beliefs or to be acted on if that is called for. We are aware that an argument occurs in a context and that contextual factors may be crucial in understanding or evaluating it. But those are not defining features. For us, argument is defined structurally as a claim backed up with evidence or reasons, or premises advanced in support of a conclusion.

By contrast the main interest of the pragma-dialecticians is in a debate between two parties – called a critical discussion – of which argumentation can form an important part. The goal is to resolve this conflict in a manner acceptable to both parties, and the means a set of rules to keep the debate on track and away from fallacious or unproductive steps. Where argument analysts are interested in the product, pragma-dialecticians are interested in the process (cf. Johnson 2000, 309-320).

All actual argumentations are multiples in a sense of single argumentation, and the locus of the distinction of types is more at the evaluation than at the analysis stage. Put another way, participants in a critical discussion must agree that certain arguments fail in order to draw the distinction between multiple argumentation and coordinatively compound. Suppose in a critical discussion the speaker advances reason B in support of claim A. When the respondent refutes this, the speaker advances C in support, and when this too is lost, D in support. This process constitutes multiple argumentation – several reasons advanced seriatim in support of A. There is no cumulative effect of B, C, and D. The speaker thought initially that B was conclusive, and responds to having to relinquish it with C. If D, unlike B and C, survives the attack of the respondent, it provides the sole support for A at the conclusion of the dialectic (Snoeck-Henkemans 1997: 80-85). Ways other than pragma-dialectics of diagraming such exchanges are found in dialogue logics (Walton 1984) and dialectical exercises (Rescher 1987, 5, 19), but none have gained the wide acceptance of the Thomas types.

Now suppose that in such a critical discussion the speaker advances claim K and insists that supporting reasons L, M, and N be considered together as establishing it. Support now for K is the sum total of what each of the three contributes individually. As noted above, coordinatively compound argumentation resembles the convergent argument in this respect. The potential for confusion here is considerable. Nothing in the argument types of the argument analysts resembles multiple argumentation. Coordinatively compound argumentation itself resembles the convergent argument while its diagram resembles that of the linked argument.

The second potential confusion is of the argument types of the analysts with the forms of formal logics. One might ask, since we have the syllogism and modus ponens, whether we even need convergent or linked arguments. So we must first note the very significant difference between argument types and the forms of formal logics. Formal logics do not deal with actual arguments in natural language like those found on op-ed pages or in letters to the editor. They do not even deal with actual statements in natural language. Their grist is forms of statement that result from holding some features of certain statements constant and allowing others to vary. Syllogistic logic, e.g., deals only with affirmative or negative statement forms beginning with “all,” “no,” or “some” that predicate a quality of a subject. “All S are P” is an example. Here “S” and “P” are variables or placemarkers for count nouns. When specific count nouns are substituted, we have what is called a categorical statement that is either true or false e.g. “All bears are mammals.” Every syllogism comprises two such categorical statements with the claim that they prove a third.

You can read several months’ worth (perhaps even years’) worth of op-ed pages and letters to the editor without ever seeing a syllogism. You will find some material which can be restated and then cut and twisted to fit a syllogistic form. But in such cases the syllogism usually has little or nothing to do with the question at hand. By contrast the argument types of informal logic are descriptive of ways in which people advance reasons or evidence in support of a conclusion. You are unlikely to find arguments on op-ed pages or elsewhere that cannot be analyzed into these types. The broad applicability of these types is a strong point in their favor.

In formal logics, certain combinations of statement forms, such as modus ponens, are taken as constituting argument forms. An important task for the formal logician is distinguishing valid from invalid argument forms. There are a number of ways of doing so, such as axiomatic, tabular, or natural deduction techniques. In the latter, some forms are assumed valid, and others are derived from them. The distinction of valid from invalid argument forms provides the formal logician with a powerful tool. If the material from natural-language argument can be cut and twisted to fit a form – a big “if” since the substance of the original must be preserved – we have a decision procedure. If the argument has a valid form and the premises are true, the conclusion must be true. If the argument has an invalid form, it cannot establish its conclusion. This does not mean the conclusion must be false, only that, if true, its truth isn’t established by this argument.

Another way of drawing this distinction is to note that a valid argument form in formal logic has probative force – substitute in true premises that fit the statement forms and you have established a conclusion. The argument types we are dealing with in informal logic have no probative force. There is no distinction of valid from invalid convergent arguments based on form. To identify an argument as one of a certain type is to note that evidence or reasons are being advanced in a certain way to support a conclusion. As we saw above, this belongs to the analysis phase of our work with an argument. Evaluation still remains to be carried out.

The forms of formal logics are unlikely to be confused with the argument types of the analysts. They don’t employ arrow diagrams and they don’t even loosely fit most argument in natural language. The potential for confusion with the argument types of pragma-dialectics is greater. The dialecticians focus on a process – dialectic is, after all, itself a process – of debate or critical discussion the goal of which is to resolve a conflict. Argumentation as captured by arrow diagrams and types can be part of this process. For the analysts, an argument – however complex – is a unit about which the most important question is whether the conclusion is established.

4. Extending the Typology
More clarity over its role in analysis may promote greater use of diagraming and types among those who work with argument. The second factor that may currently limit application is the lack of an accepted way of referring to the complex arguments that are more likely to solicit our interest and close attention(ii). The problem isn’t that the arrow diagraming technique is limited. Experienced practitioners have no difficulty extending it to arguments of ten or twenty statements. In fact, the only barrier to extending it further is that it becomes cumbersome and hence a less efficient tool for analysis.

The problem is that the typology itself needs extending so that we have a shorthand way of referring to the resulting complex diagrams. The solution I propose is quite modest for bringing no theoretical innovation (for interesting ones see Walton 1996, ch. 6) as well as tentative in that I would readily abandon it for a better should someone produce that. But it does have the virtue of building on the four basic Thomas types, which are widely known and generally accepted in North America.

There are four parts to my proposal.
1. Any argument more complex than the four Thomas types is a compound argument. Such arguments will usually be compounds comprising arguments of two or more Thomas types. Note that simply adding one more premises to a basic-type argument does not make it a compound argument. For instance, the basic convergent type is usually shown with two premises. Our above example has three premises yet remains a basic convergent argument.
2. Compound arguments will be named based on the support for their final conclusion. If two or more premises or intermediate conclusions converge on the final conclusion it will be a compound convergent argument.
3. Four compound types will be added to the five basic ones: compound linked, compound convergent, compound serial, and compound divergent. Three are illustrated below.
4. When germane to the discussion, premises can now be distinguished into those that receive no support from other premises in the argument and those that do. The former are basic support statements, the latter intermediate conclusions. Premise-conclusion relations can now be referred to as relations of logical support or, for short, support relations.

In each of the following examples, the first found by Shane Anderegg (Newsweek 2002), a comment or two on evaluation can show how evaluation should follow on analysis. More could be said on the evaluation of each, but that would take us too far from our goal of exhibiting new argument types.

Without the above proposal one is unsure what to call this argument. It can be described as a combination of two serial and two simple arguments, but this is an uneconomical way to refer to it. Since four supporting statements converge on a final conclusion we can now refer to it as a compound convergent argument. If helpful, it can be analyzed in terms of serial arguments, basic support statements, and intermediate conclusions. ? is false. Hydrogen is explosive, as survivors and investigators of mine explosions can testify. Airships switched to helium after the hydrogen-filled Hindenburg exploded in 1937, and balloons switched to hot air. Loss of one line of support needn’t destroy a convergent argument, but loss of ? and ? here makes it difficult to support the modality of the conclusion “too good to be true.” The dialectical tier might also yield factors to further weaken this argument.

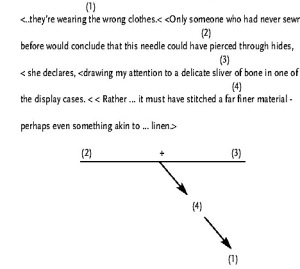
Scientific American (2000) challenges the view that pre-historic man wore mainly animal skins. Archeologist Olga Saffer, who worked ten years in the fashion industry, points to animal-skin clad cavemen in the Paris Musee de l’Homme:

The gain in terminological simplicity – from combined linked-serial to compound serial – is smaller here, and the advantage of dividing the second sentence is comparatively subtle. It separates the fact that a slender needle is indicated from the claim that it could not have pierced hides, allowing us to accept the former and challenge the latter. As my students pointed out – reminding me of the leather-working phase of scouting – people who made clothing by hand from leather used two instruments: a pointed tool called an awl for punching holes, and a needle for sewing. This fact undercuts the support of ? and ? linked for ? and yields a weak argument. It also illustrates how in a linked argument loss of one premise can greatly weaken an argument.

Finally we can glance at the application of this typology to a more complex argument paraphrased from William James’ essay “What Pragmatism Means.”(James 1967)

This argument is compound linked because the older beautiful simplicity of the laws must combine with the newer messy complexity to provide evidence for (12). I have supplied the assumed premise [6]. Without it someone might question the support for ? on the basis that features from rival theories could combine into the one theory ? rules out.

Evaluating the argument opens a different diagraming possibility. ? could receive more support – recall Newton’s space as sensorium dei – but we can provisionally accept it and ? as adequately supported or capable of adequate support. But ? is somewhat of a problem, as Joe Meredith and Nate Wallace pointed out in my advanced critical thinking class. The theory of racial superiority has been used to justify harming or killing large numbers of people, and that of scientific creationism used to ban teaching of the theory of evolution in Arkansas – you can augment this list at will. Medical science once bled the sick to restore the balance of humours, which probably killed more people than it helped in the millennia before the discovery of micro-organisms and antiseptics. ? is (at least) stated too broadly.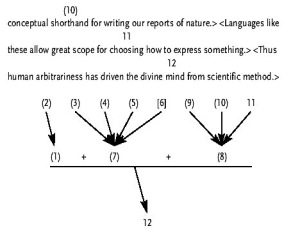

But by linking ? with other intermediate conclusions we signify that it is essential to support the final conclusion. The Principle of Charity urges us, when we have alternatives, to interpret the argument most favorably to the author. So we could link only ? and ?, allowing ? to converge on (12). The advantage of this analysis for James is that should ? and ? suffice, the questionableness of ? wouldn’t sink the argument. The disadvantage for us is that we may now be beyond the intent of James. “Artitrariness” in (12) is his term, and ? seems required to support it. If it were our argument – which it isn’t – we might substitute “human choices have” for “human arbitrariness has” and have a strong argument for much of what James sought to establish.

5. Conclusion
When we divide our work on discourse that appears to be argument into identifying, analyzing, and evaluating the argument, arrow diagraming and the resulting types of Thomas fall into the analysis phase. Once the type is identified, a new set of questions about the reliability and relevance of the premises, effect of the context, and modality of the conclusion must be addressed to evaluate it. So these types differ greatly from the forms of formal logics, where the only question remaining when an argument instantiates a valid form is whether the premises are true. The diagrams of the linked and convergent arguments resemble those for coordinatively compound and multiple argumentation of pragma-dialectics, but the argument types are quite different. Those of the pragma-dialecticians are regarded as parts of a debate whose two parties must abide by rules to resolve their conflict.

My proposal for extending the Thomas typology is to add four compound argument types: compound serial, compound convergent, compound linked, and compound divergent. Plus one basic type: the simple argument. I also suggest a vocabulary comprising final conclusion, intermediate conclusion, basic support statement, and relations of logical support or support relations to label components of the compound arguments. Some of these are illustrated in arguments analyzed above. My hope is that the advantage of naming and discussing the complex arguments they diagram will facilitate use of arrow diagraming and its types among informal logicians working on actual arguments of interest to them. And further, that by their example and their teaching, this technique will spread further among the educated public where facility in dealing with argument has scarcely ever been in greater need.

NOTES
[i] In commenting on the version of this paper read at the ISSA 2002 Conference.
[ii] I believe Leo Groarke noted a need for this in his presentation at the 2001 conference of the Ontario Society for the Study of Argumentation in Windsor, Ontario.

REFERENCES
Beardsley, Monroe C. 1975. Thinking Straight, 4th ed. Englewood Cliffs: Prentice-Hall.
Eemeren, Frans H. van & Rob Grootendorst. 1984. Speech Acts in Argumentative Discussion. Dordrecht: Foris.
Freeman, James F. 1999. Argument Structure and Disciplinary Perspective. In Frans H. van Eemeren et al., eds., Proceedings of the Fourth International Conference of the International Society for the Study of Argumentation. Amsterdam: SicSat, 208-211.
Hoaglund, John. 1999. Informal Logic: The Two Schools. In Frans H. van Eemeren et al., eds., Proceedings of the Fourth International Conference of the International Society for the Study of Argumentation. Amsterdam: SicSat, 348-352.
Hoaglund, John. 2000. Reasoning and Giving Reasons. Australasian Journal of Philosophy, 78, 575-594.
James, William. 1967. What Pragmatism Means. In The writings of William James, ed. and intro. by John J, McDermott. Chicago: University of Chicago Press.
Johnson, Ralph H. 2000. Manifest Rationality. Mahwah NJ: Lawrence Erlbaum Associates.
New Republic. 2000. March 27.
Newsweek 2002. April 15. Hope Springs Eternal..
Rescher, Nicholas. 1987. Dialectics. Albany: SUNY Press.
Scientific American. 2000. The Caveman’s New Clothes. Nov., 32.
Snoeck-Henkemans, A.F. 1997. Analyzing Complex Argumentation. Amsterdam: SicSat.
Thomas, Stephen N. 1996. Practical Reasoning in Natural Language, 4th ed. Upper Saddle River NJ: Prentice-Hall.
Walton, Douglas. 1996. Argument Structure. A Pragmatic Theory. Toronto: University of Toronto Press.
Walton, Douglas N. 1984. Logical Dialogue Games and Fallacies. Lanham MD: University Press of America.
www.bloomington.in.us/~stopcrop/problem.html.
Yanal, Robert J. 1984. “Convergent” and “Linked” Reasons. American Philosophical Association Newsletter on Teaching Philosophy. Summer, 1-3.

You May Also Like

ISSA Proceedings 2006 ~ The Criminal Abduction Paradox

ISSA Proceedings 2006 ~ A Discussion Of Habermas’ Reading And Use Of Toulmin’s Model Of Argumentation

ISSA Proceedings 2006 ~ The Rules Of The Critical Discussion And The Development Of Critical Thinking

ISSA Proceedings 2006 ~ An Analysis Of Preschool Hebrew Speaking Children’s Arguments From The Perspective Of The Pragma-Dialectical Model

ISSA Proceedings 2006 ~ Putin’s Terrorism Discourse As Part of Democracy And Governance Debate In Russia

ISSA Proceedings 2006 ~ Cultural Differences In The Persuasiveness Of Normatively Strong And Normatively Weak Expert Evidence

Comments