In the following paper I focus on some rhetorical practices that are used by interactants in arguments with others. I identify argument criteria interactants refer to and describe how they use them as interactional resources for their argumentation. My considerations are part of a broader study of conversational rhetoric in problem oriented and conflict interaction, conducted at the Institute for German Language in Mannheim, Germany (see Kallmeyer 1996). The main goal of this project is the analysis and description of interactive practices under a functional rhetorical perspective which is derived from an ethnomethodological approach to the study of conversation. Ethnomethodologists have so far mainly looked at the organizational order of interaction (see Garfinkel & Sacks 1970), we also investigate on forms of interactive influence and interactive effects of the participants’ interactive work.

In order to describe a wide range of rhetorical practices we take into account various dimensions of interaction that have been explicated by Kallmeyer and Schütze in a theory of the construction of interaction (Kallmeyer & Schütze 1976). According to this theory interactants have to carry out their conversation by simultaneously dealing with different dimensions of interactional organization (listed in Figure 1):

Organizational structure of talk
Thematical organization
Activity organization
Identity and relationship construction
Modality construction
Reciprocity organization

Figure 1 Dimensions of interaction construction

Concerning rhetorical practices, there are for example different practices of cooperation and constraint that are required due to the organizational structures of talk, or practices of social positioning of the participants due to identity and relationship construction, or practices of setting and blocking perspectives due to reciprocity demands. The context of my argumentation analysis is the dimension of thematical organization in problem and conflict interaction. Argumentation as a whole is seen then as one rhetorical practice for thematical clarification amongst other patterns such as for example story telling, reports, or portraying (see Kallmeyer & Schütze 1978). Thus, first I had to analyze argumentation as a whole and to work out the conditions under which argumentation is established and carried out in interaction.
Briefly put, interactants begin an argumentation when their thematical exchange runs into a deficit. Then they have to explain and give reasons. Typical deficits include dissent or uncertainty. Argumentation, then, is an interactive pattern for explaining a position and for locally clarifying the deficit and for then integrating the solution of the deficit into the „normal“ course of the current interaction. Formally characterized, argumentation has a three part structure consisting of initiating, carrying out and reintegration. I do not want to specify the difficulties of the empirical analysis of the argumentation pattern but to focus on argumentative relevances that interactants deal with during their argumentation. In the course of that I will point out resources of argumentation which are made relevant from the participants themselves in rhetorical argument practices.

Before presenting these resources and practices I will briefly explain the methodology that we have used. First of all, I defined segments of argumentation in about sixty video- or audiotaped and transcribed conversations from a wide range of problem and conflict interaction situations such as mediation talk, mother-daughter or partner-conflict talk, counselling sessions, TV-discussions, and so on.[i] Within these segments I looked for either explicit complaints  or particularly expanded formulations produced by the interactants. These activities were analyzed in a pragma-semantic perspective for criteria that the participants themselves make relevant as argument criteria. They complain about incorrect argumentation moves of their respective partners, or otherwise characterize some of their own activities as particularly important. In this fashion, I use the participants’ perspective in my methodical approach.
In this fashion, I could identify two groups of criteria or resources of argumentation: one group which reflects certain conditions and organizational constraints of conversational argument, and another group where the interactants exchange thematical moves in different modality formats as arguments.

I will now present the criteria in both groups in a synoptical way, and explain them and their relation to the different dimensions of interaction. I will thereby shortly indicate how interactants use these criteria as resources to construct rhetorical practices for their argumentation. After that I will give some examples of some of these practices, their formats, linguistics, and their positive or problematic interactive effects.

The first group, which reflects certain conditions and organizational requirements of conversational argumentation, contains the following five criteria:
1. Interactants demonstrate thematical consistency and consistency of their utterances, they check it, or they complain about inconsistencies of their partners’ argumentation. Consistency refers to contradictions and (in)coherencies and is seen both, locally and globally in the course of argumentation. Dealing with consistency is relevant in the dimension of thematical organization.
2. Interactants demand interactional relevance of the partners’ activity, or they deny it. Relevance is a very strong and often-used argument. Interactants always organize the course of their mutual argumentation by referring to relevance. Relevance as a criterion or an argumentative rhetorical resource belongs to the dimension of activity organization (which includes a wide range of activities from a single speech act to the global activity tasks, such as for example, counselling or mediating).
3. Another criterion operates in the same dimension of activity organization: argumentants make sure that their activities are appropriate and valid in relation to the global activity tasks and to the thematic development oft the argumentation. Otherwise they critizise the inappropriateness and invalidity of the partners’ argument.
4. Argumentants also use qualities of identity as argument criteria. One important criterion then is, whether the partners are competent to deal with the discussed topics or not. In argumentation the partners demonstrate their competence, for example, by deriving it from personal experience, or from professional knowledge; they attribute competence to their partners or they deny their partners’ competence. Discussions of the respective partners’ competence operates in the dimension of identity and relationship construction in interaction.
5. Also in this dimension, a further criterion operates which argumentants take into consideration: argumentative integrity. Interactants demonstrate in argumentation that they are trustworthy and authentic, that they pay attention to the partners’ interactive rights and so on. Or they critizise their partners for ignoring such integrity demands.

The second group of argument criteria is at the heart of argumentation. Interactants exchange thematical activities in different modality formats as arguments. This group of interactive arguments deals with epistemic or deontic modes and therefore operates in the interactive dimension of modality construction.

6. Primarily, argumentants deal with factuality. They claim what they are saying as real or factual. And they sometimes even demonstrate the factuality of their assertions. Otherwise they also deny factuality of their partners’ assertion. And they do so in an epistemic mode of objectivity.
7. In contrast to the presentation of objectivity argumentants also claim a subjective epistemic mode. They characterize what they are saying as subjective, for example, as their personal conviction. They also formulate assumptions and demand their partners’ assumptions.
8. And, finally, argumentants deal in a deontic mode with normativity: while arguing they appeal to social norms, they estimate their own or their partners’ arguments in relation to such norms, or they put in a normative claim regarding their partners’ activities.

The criteria and rhetorical practices that I have mentioned in this synoptical fashion reveal the fundamental characteristics of discursive argumentation. These are not meant as exclusive categories: for example, competence sometimes interferes with integrity or with relevance in such a way that critizising disintegrity also aims at denying competence, or the alleged lack of competence also makes an activity irrelevant – language use is always ambi- or even polyvalent. But in analyzing argumentative discourses you will regularily find these criteria and practices (listed in figure 2) and you can exhaustively analyze with them the argumentative exchange in discourse.

Figure 2 Argument criteria and rhetorical practices

In a discourse analytic perspective you have to bear in mind, however, that argumentants do not really work out what is true or right. None of the above categories has any argumentative ontological state. Argumentants otherwise always do interactively negotiate what is fact, which norm is right, what is relevant for them and so on. Interactively valid is only what argumentants accept by arguing interactively (see Deppermann 1997, Chs. I.2.5 and III.4).

In the following section I will shortly present two of the rhetorical practices of argumentation. As a first rhetorical practice I will explain denying competence. Interactants mutually have to attribute competence for the global tasks of their interaction (see Nothdurft 1994). Competence is on the one hand a logically necessary condition, but on the other hand locally negotiable in detail by the interactants. To demonstrate competence provides validity to the discursive activities while denying competence withdraws trust in the partners’ utterances. By dealing with the criterion of competence speakers claim validity, make the partners’ claims problematic, or even reject them. Competence is seldom a central focus in argumentation but it is an important criterion for judging. Dealing with competence therefore is a referring and a pivotal activity: it refers to an activity of the speaker or his partners, and it regularily paves the way for the speaker’s following own activities.
Denying competence refers to personal qualities like age, job, social role, discursive abilities, and so on. Sometimes interactants critizise problematic, deficient, or irrelevant competences of their partners, sometimes they say that their partners have no competence at all. Problematic or even „wrong“ could be a competence which is related to personal interest (for example, if a manager of the tobacco industry defines the dangers of smoking cigarettes; for the other qualities of incompetence as deficient, irrelevant or not existing you may simply build examples of your own.

A denial of competence is uttered when speakers explicitly reserve some competence only for their own, or if the partner’s arguments implicitly make claims for competence. The rhetorical practice of denying competence is rather seldom in argumentation because it is a face-threatening activity. But sometimes in interactions before an audience, denying competence makes sense for the critic as a demonstrative act directed to the audience.
Denying competence as an argument practice is a powerful resource to block the partner’s move and to establish one’s own activities. It is dysfunctional if the face-threatening aspect overwrites the focal interactive tasks.
As a second example I will explain a practice by which the speaker claims a particular epistemic modality for his own activities: claiming factuality. In argumentation the common view on reality is fragile, there is dissent or uncertainty between the partners. Argumentants then try to reestablish a common perspective by making assertions with which they try to bring about acceptance by their partners. Assertions and their acceptance do oblige the interactants then to a common view.
Presupposing the possibility of such an agreement is a central premise for being able to interact at all. The interactive power of the epistemic mode of factuality is grounded in the assumption that other persons are able to perceive things like I do. Argumentants deal with this, but you have to notice that reality also is a discursively negotiable entity and not an objective entity that one can simply refer to.
The overwhelming part of argument activities in discourse deals with claiming factuality. Speakers regularily use agreements about aspects of reality to make clear and to consolidate their own argumentative positions or otherwise to undermine the partner’s position. The relations of all assertions thereby build up a network of a global position, they help to support other assertions and as a whole they make the discursive presentation itself scrutinizable, for example, via the probe of coherence and contradiction.

By claiming factuality the interactants try to interactively establish the validity of propositions and to push through their interest. Claiming factuality is normally realized by existential propositions. Such utterances are often self-evident and interactively ratified or even accepted in an unproblematic way. However, at the end of longer contributions, especially as conclusions, they are often rejected by partners because they claim global positions. Linguistically, the factuality mode is established by the indicative sentence mode. Lexically, you often find markers like „indeed“, „really“, or „literally“ and so on. Prominent also are some prosodic features which range from unmarked self-evidence to marking certainty by accent, pitch, and rhythm.
Claiming factuality always establishes the necessity to deal with it. Partners are forced to react either by ratifying or accepting, or by rejecting it. Accepting on the one hand then obliges partners for the further discourse while rejecting leads to a – normally dispreferred – expansion.
The interactive constraint to deal with this practice by ratifying, accepting or rejecting produces its own rhetorical power: Every claim stabilizes an argumentative position of the respective speaker. With it, aspects of a supposed reality are interactively publicized and asserted, and the inferential implications produce local and global effects. But the speaker himself is also bound by his or her own statements, and, besides, such assertions and their respective global position always are threatened by contradicting claims of their partners.

NOTES
i. The corpus reperesents a selection from the corpora of the Institute for German Language, which include some hundred natural conversations.

REFERENCES
Deppermann, A. (1997). Glaubwürdigkeit im Konflikt. Rhetorische Techniken in Streitgesprächen. Frankfurt et al.: Peter Lang Verlag.
Garfinkel, H. & H. Sacks (1970). On formal structures of practical actions. In: Y.S. McKinney & E.A. Tiryakian (Eds.), Theoretical sociology. New York: 337-366.
Kallmeyer, W. (Ed.)(1996). Gesprächsrhetorik. Rhetorische Verfahren im Gesprächsprozeß. Tübingen: Gunter Narr Verlag.
Kallmeyer, W. & F. Schütze (1976). Konversationsanalyse. Studium Linguistik 1, 1-28.
Kallmeyer, W. & F. Schütze (1977). Zur Konstitution von Kommunikationsschemata der Sachverhaltsdarstellung. In: D. Wegner (Ed.), Gesprächsanalysen. (pp. 159-274), Hamburg: Buske Verlag.
Nothdurft, W. (1994). Kompetenz und Vertrauen in Beratungsgesprächen. In: W. Nothdurft, U. Reitemeier, P. Schröder (Eds.), Beratungsgespräche. Analyse asymmetrischer Dialoge (pp. 184-229), Tübingen: Gunter Narr Verlag.
Spranz-Fogasy, T. & T. Fleischmann (1993). Types of dispute courses in familiy interaction. In: Argumentation. An International Journal on Reasoning 7, 221-23.

In this paper I shall discuss a fallacy involving dividing by zero.  And then I shall more briefly discuss fallacies involving misdrawn diagrams and a fallacy involving mathematical induction, I discuss these particular fallacies because each of them seems at first – and seemed to me myself at one time – to be a counterexample to a theory of mine. The One Fallacy Theory says that every real fallacy is a fallacy of equivocation, of playing on some sort of ambiguity. But these particular fallacies do not seem to involve ambiguity, and yet they do seem to be real fallacies.[i] Let me begin with the dividing-by-zero fallacy.

It goes as follows:
1. Let a = b
2. So a2 = ab (multiply each side by a)
3. So a2 – b2 = ab – b2 (subtract b2 from each side)
4. So (a + b)(a – b) = b(a – b) (factoring)
5. So a + b = b (cancelling (a – b) on each side)
6. So 2b = b (since a = b)
7. So 2 = 1 (cancelling b on each side).

Now this argument appears to be a counterexample to my theory. Each step is stated in unambiguous algebraic terminology. The invalid move takes us from an unambiguously true equation 4 to an unambiguously false equation 5 by a move of cancelling a -b which is unambiguously though not obviously a division by zero. There seems to be no ambiguity.

My theory then seems to imply that there is no real fallacy; we do not have an invalid step which appears, by virtue of a covering ambiguity, to be valid, but rather a naked mistake with no appearance of goodness. A naked mistake is not a true fallacy.
But surely, the argument is a real fallacy. For it passes the phenomenological test. The first time I myself saw this argument in a book, I went through it carefully looking for the wrong step. And I could not find it, at least not just by going through the argument step by step. It looked like a proof to me, and at a time when I knew there had to be something wrong and was, in an intellectually serious way, looking for the mistake!
So clearly the argument is a real fallacy. It therefore seems a counterexample to my theory.
Now in trying to defend my theory, I think as follows. If a serious person is taken in by an invalid argument A/ .. B and ‘A’ and ‘B’ are not ambiguous, perhaps there is some other reasoning in the person’s mind. Perhaps he thinks that A implies C and C implies B, and it is the interpolated term C which is ambiguous. Another person who accepts A/ .. B may accept it for a different reason, using a different confusion, say A/ .. D/ .. B.

I therefore ask: Why did I myself think the argument dividing by zero was valid step by step?

It is often said that people divide by zero, as in our example, because you can usually divide and people just forget about the special case of zero. I have never liked this kind of explanation. How can one just forget about special cases? If the rule is that you can always divide unless the would-be divisor is zero, how can one apply this rule without determining whether the would-be divisor is zero?
At any event, the explanation about forgetting the special case did not apply to me. I didn’t forget the special case. I had never heard of any such special case. I learned from studying this very fallacy that one can’t divide by zero. I was astounded to find that one couldn’t always divide! I thought that you could always divide and that I knew you could always divide.

Now here too there is a popular explanation about why people think they can always divide. The explanation is that people overgeneralize: since you can almost always divide, we overgeneralize and thin we can divide in the case of zero also. I do not like this explanation. Such inductive reasoning could easily lead a rational person to think that one can always divide, probably. However, mathematical knowledge is not about what is probably true but about what is proven. I thought I knew that one can always divide, that I had seen a proof of this.
Now after examining the argument and not finding the mistaken step, I substituted the concrete number 5 for a and b. The equations then became: Let 5 = 5. So 25 = 25. So 25 – 25 = 25 – 25. Upon factoring, 10 { 0 = 5 { 0. Cancelling, 10 = 5. So 10 = 5. So 2 = 1. And here it is obvious where the mistake is. The equation 10 { 0 = 5 { 0 balances, but 10 = 5 doesn’t.
And reflecting on this wrong move, we see that its general form is x { 0 = y { 0/ .. x = y. So if we can divide by zero, then all numbers are equal. This proves that we cannot divide by zero. Of course, when I saw this, I distrusted my reasoning and went and looked in a math book to assure myself that it was really true that you can’t divide by zero.

Having thus decided that you can’t divide by zero, I started to consider my reasons for thinking you can divide by zero. How can it be that we can’t divide by zero? After all, I first thought, multiplication is always well-defined. But division is defined as the inverse of multiplication. Doesn’t it follow that division is always well-defined as well? I knew immediately that there was something wrong with this reasoning. In the natural numbers, it is always possible to add but one cannot always subtract, say, 7 from 3. Yet subtraction is defined as the inverse of addition. How then can it be that one can’t always subtract?

To understand this fallacy more clearly, let me state my argument in more sophisticated terminology. In modern logic, definite descriptions are well-formed expressions whether they refer or not. Thus, in a Russellian sense, ‘the king of France’ is a well-defined expression. And so, for any x, is ‘(¡ z)(x = z { 0)’. But the latter is the definition of ‘x/o’, which is thus well-defined, in a Russellian sense. For Frege, however, a referring expression is not well-defined unless it is proven that it actually succeeds in referring to something. Mathematicians speak of functions as being ‘well-defined’ in Frege’s, not Russell’s sense. If x/o were well-defined in Frege’s sense, then division by zero would be possible. So my argument involved an equivocation, on two different meanings of ‘well-defined’.

When, years ago, I fell into the dividing-by-zero fallacy, I found that one can’t divide by zero, and asked myself ‘how can that be?” I then went through the ‘well-defined’ problem as just rehearsed. However, when I saw that there were two different concepts of ‘well-defined’ involved, I did not feel that this point really addressed my perplexity, for I thought I had somewhere seen a proof that division always was well-defined, even in Frege’s sense. Hadn’t I seen a proof that you can always divide? Before looking at the proof I had in mind at that time, it is convenient here to consider another possible supposed proof.
In a book, Lapses in Mathematical Reasoning, the authors, Russian mathematicians, mention fallacies in which a true mathematical law is applied but in the wrong field of numbers. (Brades et. al. 1963: 14) It is interesting that fallacies involving dividing by zero can be thought of as a subclass of those applying a true law in the wrong field of numbers, and these in turn are a subclass of fallacies of ambiguity.
When we learn about numbers in our school years, we learn to use the word ‘number’ ambiguously. At first the teacher says that numbers are those things you count with: 1, 2, 3, 4, etc. So we learn to use ‘number’ to mean a natural or whole number, a positive integer. In this sense of ‘number,’ we learn that we can always add and always multiply, but we cannot always subtract or always divide. For instance, we cannot subtract 7 from 3 or divide 3 into 7. But then later the teacher told us that, after all, we could always divide as well as always add or multiply, though we still could not always subtract. We could now always divide because, the teacher said, “there are more numbers than you yet know about.”
Even as a youngster, I was rather hyper about ambiguity, and I said – though to myself, not out loud – “Come on, teacher, there aren’t more numbers than we know about. The truth is: you’re going to change the meaning of the word ‘number’”. And so it happened. Now ‘number’ meant positive rational, the fractions were numbers, and we could always add, multiply, and divide. With ‘number’ in this meaning, any number whatsoever could be divided by any number whatsoever, without any exception whatsoever.
Later the term ‘number’ will be extended again, from the positive rationals to the rationals generally. Now subtraction will always be possible, as well as addition and multiplication, but division by zero will not be possible.
And so one fallacious way of dividing by zero would be to apply the true law that division is always possible – true in the positive rationals, but to apply this law wrongly to rationals generally. This way of dividing by zero would involve equivocation on the term ‘number’ and so would be in accord with the One Fallacy Theory.

Still, when I myself divided by zero, I did not do it in this way, I believe. I knew that ‘number’ was ambiguous. I knew that when you extend the number system, as from positive rationals to rationals generally, in order to make a new operation, as subtraction, always possible, you have to recheck the previously always possible operations – addition, multiplication, and division – to make sure they are still always possible. But I thought I had seen in my readings just such a rechecking, a proof that these operations were always possible in the rationals generally.
So I recalled the argument in question. Take addition. Addition was always possible in the positive rationals and subtraction is now always possible. So let a and b be positive. Then a + b always exists. But a + (-b) is a – b and also always exists. And (-a) + (+b) is b – a and always exists. And, finally, (-a) + (-b) = -(a + b), a negative, and always exists. So addition is always possible, it seems. But the exact same argument can be given for multiplication and division. So they are all always possible.
Of course, the mistake in this argument becomes clear when we look at the version concerning division. But it is already there in the argument for addition. By considering a and b and -a and -b, I consider the positive numbers and the negative numbers but I forget to consider zero. What about zero!?
But this seems rather embarrassing. I said at the outset that I didn’t like the explanation that people divide by zero because they simply forget the special case of zero. Yet here I seem to have done precisely that! I just forgot about zero. How could I just forget about zero??

If there are three kinds of numbers, the positive, the negative, and zero, then in order to prove something about all numbers, you have to prove it about all three kinds, and not just about two. If there are three people, Arthur, Barbara, and Carl, in a room and I argue that all the people in the room are tall because Arthur is tall and Barbara is tall and I just forget about Carl, who is short, then that argument is not a fallacy; it is just a stupidity. Surely I couldn’t have just forgotten about zero!
Actually, I don’t think I just forgot about zero in the above reasoning, rather I vaguely thought I had covered zero twice over, though in fact my reasoning was not valid for zero. For I tend to use the terms ‘positive’ and ‘negative’ both strictly, excluding zero, and loosely, including it. So by proving something for all positives and negatives, I vaguely felt I had proven it for zero.
First, zero seems positive in some ways. It is a square number, equal to 02. It is its own absolute value. It is the end point of the positive half of the real line. By the familiar end point ambiguity, an end point seems both to be and not to be a point of the line segment whose end point it is. Also the positive and negative segments are two halves of the real line, and two halves seem to complete the whole. And if zero seems to be positive, then -0, which is also 0, seems also to be negative.
Given that 0 seems in some ways to be positive and negative, the basic reason I tend to use these two terms ambiguously is because it is convenient. We wish to prove results about an infinite class of things, the numbers. We cannot prove results about the numbers one by one, so we divide them into large classes, such as the positives and the negatives. If it happens that there are special cases, such as zero, which do not exactly fit into these large classes, we tend to include or exclude the special cases into the large classes. For the purpose of one proof, we think of zero as positive, for another, as negative, for another as both or neither.
We have a tendency to stretch and contract the more general class terms to include and exclude the special cases, as convenience dictates. This, I think, is why the argument that we could always divide in the rationals generally sounded correct to me. As I said, when I proved the result for all positives and all negatives, I vaguely thought I had covered zero twice over. This general sort of fallacy, shuffling the special case in and out of the general classes, I shall call the ‘special case fallacy.’ It turns out that a variant of this fallacy is used in the remaining two fallacies I wish to discuss.
Misdrawn diagram fallacies in geometry seem at first to be counterexamples to my theory. The problem is in the misdrawn diagram, not in any ambiguity in the language used in discussing the diagram. Yet I clearly remember being shown an argument involving a misdrawn diagram and being unable to see the error in it. However I shall I argue that the diagram itself is a representation and therefore can be ambiguous. In other words, the diagrams are not really misdrawn so much as misinterpreted.

In looking over various examples of this sort of fallacy in the Lapses book, I did not find one simple enough to present here in detail. However the ones I looked at generally had a common form. In the givens we are told that there is a point with property P. Call this point A. We are told also that there is a point with property Q. Call this point B. We represent this by drawing two representing points, labelled ‘A’ and ‘B’. In the reasoning which follows, we are asked to consider the line from point A to point B. We show that this line has property X. Then we show it has property not-X. We seem to have proven a contradiction.
The solution is that point A and point B are the same point. So there is not line from A to B. (Brades 1963: 22) The fallacy can be thought of as an example of the special case fallacy. When we originally draw the representing points ‘A’ and ‘B’, these are floating points which may or may not coalesce. They represent that there is an A and a B, which may or may not be identical.
Given A, then B may be the same as A, the special case, or anywhere else, the more general subcase. So the representation assimilates the special case to the general case; the two points, so to speak, may be one. But then, when we agree to draw a line from A to B, we misinterpret the representation as representing that A and B are different, two strictly, the more general subcase excluding the special case.
Therefore it is a fallacy of ambiguity, after all: the ambiguity of the representing diagram.

A very similar analysis can be given for the last fallacy I want to look at. Here we set out to prove that all horses are the same color.373 We ‘prove’ this by ‘proving’ by mathematical induction that, for any n, any n-membered set of horses has the same-color property, namely the property that all its members are the same color. The ‘theorem’ is obvious for n = 1, for any set of only one horse has all its members the same color. So we need to prove the inductive step: if every n membered set has the same-color property, so does any n + 1 membered set. We illustrate the argument for n = 5, n + 1 = 6, but this case is to stand in for general n and n + 1. We have a set of five horses and a sixth horse. All the 5 horses are the same color. Remove the first of the 5 and consider all the remaining horses. These again are 5 horses and all have the same color. Therefore all 6 horses are the same color. QED. So all horses are the same color.

Now the mistake in this ‘proof’ is that the argument for the inductive step works for any n and n + 1 with n more than 1, but does not work when n is 1 and n + 1 is 2. We do not notice this because, I think, we abstract from the 5 and 6 case a mental picture which plays the role of a misleading diagram.

This picture looks like this:

Here the first big dot is the first horse. The second is the n + 1 horse. The three dots represent whatever is left of the n horses, the first excluded. The ambiguity in this representation is in the meaning of the three dots. It originally represents all but the first of the initial n members, if there are any but the first. It is then misinterpreted as meaning that there are such remaining members. Initially the special case of there being no remaining members is included, but then it is excluded. So here again we have a special case fallacy, and we also have a misdrawn – or really misinterpreted – diagram fallacy, although now the diagram is not actually drawn, but is a mental picture.
In this paper, I have considered three mathematical fallacies which at one time I thought were counterexamples to my One Fallacy Theory. In each case, I have argued that these fallacies can be analyzed as fallacies of ambiguity after all.

NOTES
[i] My thanks to R. De Souza, who chided me about holding a theory to which I seemed to know counterexamples. His comments led me to explore these examples more thoroughly.

REFERENCES
Brades, Vm., Minkowski, Vl., Kharchiva, Ak., translated by J. J. Schorr-Kon (1963, originally published 1938). New York: MacMillan.

A theory of argumentation is underwritten by a philosophical conception of reasonableness. This standard of reasonableness takes into account the normative character of argumentation. That is, participants engaged in argumentative discussions (of all sorts) assert and defend normative judgments not only about the content of the reasons put forth, but also issue normative evaluations of the character of their own and their interlocutors’ reasons. A philosophical conception of reasonablness explicates the sources, conditions, and consequences of the explicit as well as tacit criteria participants (including argumentation theorists) use to render normative judgments about the form and content of reasoning practices.
Given the fact of reasonable pluralism, democratic legitimacy must be constructed from the process of public justification in the face of social controversy rather than found in the contents of a universal reason, the procedures of rational choice, the conditions set out in natural law cosmologies, or the laws set out in a deep-structure social theory (Unger, 1987). That is, an account of democratic legitimacy is underwritten by a theory of argumentation and a philosophical conception of reasonableness; hence, the importance of accounts of public justification in contemporary liberal-democratic theory. One of the most pressing task for liberal democratic theory is the construction of a conception of reasonableness that could guide persons in their projects of constructing ways to live together in the face of pluralism in a just manner. It is at this point that a theory of argument and a theory of deliberative democracy need to converge.
While the field has geometric, anthropological, epistemic, and critical-rationalist accounts of reasonableness it has yet to formulate a public/political conception of reasonableness. Such an account would focus on the critical functions invocations of reasonableness plays in actual instances of public justification. I contend that the ideal of public reason as set out by Kant and Rawls, if amended to account for the critical use of the concept in actual argumentation, provides a good starting place for formulating a public-political standard of reasonableness. I begin by examining some of the ways in which reasonableness is conceptualized in argumentation theory and advocate a conception attuned to the ways reasonableness is used as a critical standard by participants to regulate argumentative discussions. I then sketch how the ideal of public reason can be amended to serve as a public/political conception of reasonableness that underwrites a deliberative account of democracy.

1. Reasonableness: Epistemic and Critical Conceptions
Often tacit in our argumentative practices and manifest in our philosophical reflection is the distinction between the reasonable and the rational. When we act “rationally,” we pursue our self-interest in an manner that follows from a set of logically derived principles that do not take into consideration the beliefs, knowledge, experiences or interests of others unless they are central to the maximization of our own interests. That is, to act rationally is to act in an instrumentally intelligent, self-interested way. To act reasonably, on the other hand, is to “restrain our pursuit of self-interest by acting in accordance with principles that fix fair terms of cooperation” (Keating, 1996: 312). Reasonable people reconcile conflicting aims and interests by looking for the terms by which their actions would be judged as legitimate by others in their community and to the best of their ability regulating their actions in light of those terms.
The social and situated character of reasonableness is often cause for conceptualizing reasonableness in descriptive terms while those prone to conflate the rational and reasonable conceptualize reasonableness in normative terms. I think this is a mistake for two reasons: a purely descriptive or normative account of reasonableness is inadequate and both fail to recognize the “critical” functions standards of reasonableness play in argumentative discussions.
A purely descriptive account of reasonableness, one that seeks only to describe the accounts of reasonableness prevalent in particular discursive communities, is incapable of guiding evaluations of argumentative practices. That is, it is “empty” to the extent that it can’t tell us the difference between a good and bad argument or between a legitimate or illegitimate practice. Thus, in terms of democratic legitimacy, there may be illegitimate regimes that would be judged as legitimate based on the prevalent beliefs, no matter how misguided or corrupt, of the population as well as legitimate regimes that would be judged as illegitimate.
On the other hand, a purely normative theory, one that is not concerned with the existing standards of reasonableness constituting a community but only with setting out an ideal standard by which to judge argumentation, is vulnerable on two counts. First, it presupposes that there is a univocal reading of what constitutes reason. Yet if there are reasonable disagreements about the demands of reason itself, assuming that reason can not and does not univocally dictate our beliefs, desires, and inferences, then a purely normative account of reasonableness will be incapable of justifying itself in light of the pluralism of reason. That is, it will be seen by some as unreasonable. Second, in terms of the place of public justification in constructing democratic legitimacy, a purely normative account would be anti-democratic to the extent that it was not an organic extension of the peoples’ reason but a standard paternalistically imposed from above.

The problem with both descriptive and normative accounts of reasonableness is that they fail to take into consideration the fact that reasonableness is a concept that is invoked by participants in argumentative discussions (again, I include argument theorists in this class) to do critical work. I think this is due to the tendency of both descriptive and normative theories to conceptualize reasonableness in epistemic terms. Arguments, from an epistemic perspective, aim at the achievement of justified assent, of warranted knowledge. Reasonableness, then, is defined in terms of what would be deemed as an epistemically serious, where the premises warrant the adoption of the asserted standpoint, justification by a rational judge (Siegel & Biro, 1997). Epistemic accounts of reasonableness begin by defining argumentation as oriented to producing mutual knowledge via an organized process of critical discussion. The analytic task is the specification of what it is that interlocutors come to know as the result of argumentation, with the specification of that object of knowledge as the realization of the analyst’s explanatory goal (Taylor, 1997). This object of knowledge refers the focus of normative accounts like Siegel and Biro’s (1997), as well as the interactional knowledge necessary to achieve a resolution of a difference of opinion; hence, the rules and units frame-work endemic to Pragma-dialectical accounts. Thus, reasonableness becomes a property of either arguments or speech act complexes. That is, we say that a particular premise or set of rules is reasonable inasmuch a rational judge deems them so. A rational judge would evaluate arguments and critical discussions in light of an apriori specified system of epistemic principles or codes of conduct that determines the reasonability of an argument. But who determines the reasonability of the principles and codes of conduct used by the rational judge to evaluate argumentation? It seems that given the pluralism of reason this conflation of rationality and reasonableness in epistemic accounts, in both their descriptive and normative variants, constantly deflects our attention away from the methods that participants employ to ascertain and accomplish reasonableness, that is if the arguments and the arguers actually respect the fair system of cooperation designed to handle the interminable plurality of beliefs in a democratic society, to the task of delineating the hypothetical object known in common (a set of beliefs, epistemic standards or codes of conduct) by the interlocutors producing argumentative discourse. Yet, this object known in common is necessarily unspecifiable or empirically unverifiable given the fact of reasonable pluralism extends to the demands of reason itself.

The problem with the conflation of the rational and the reasonable in epistemic accounts is that reasonableness is lost as a standard of judgment interlocutors use in the moment-to-moment unfolding of argumentation. Rather, reasonableness becomes a standard that is leveled after the fact and from outside the actual argumentation to determine its worth. The fact that reasonableness has no specification outside the particular principles of rationality posited by a particular argumentation theory or administrative system makes it an especially powerful tool for justifying any number of social policies. For instance in a study of the U.S. Supreme Court decisions surrounding hostile environment sexual harassment claims it became apparent that the court used the standard of reasonableness to justify a series of contradictory decisions as well claim the legitimacy of social processes that routinely silenced the claims of women and minority plaintiffs (Hicks & Glenn, 1995). This was not because the standard of reasonableness used by the court was not sufficiently normative; to the contrary, it was because the standard had no meaning that was separate from the legal principles used in that case.
I wish to reclaim reasonableness as a critical standard invoked by participants in argumentation. By a critical standard I mean that reasonableness is used both normatively and reflectively by participants to manage the shape and trajectory of critical discussions. That is, arguing about reasonableness and using a philosophical conception of reasonableness to evaluate the form and content of each other reasons and conduct is a feature of argumentation itself. By employing reasonableness as a normative meta-discourse for talking about what they and their fellow interlocutors do, arguers categorize and characterize; they impose a descriptive grid on argumentative conduct and its agents (Taylor, 1997). Arguers do not simply invoke and dispute standards of reasonableness for the sake of description. In invoking a standard of reasonableness arguers are evaluating the character of the arguments, the event of argumentation and the agents involved in the argumentation. Participants invoke reasonableness to make distinctions between their own and others’ claims, to justify not having to answer particular claims, as a reason to support particular claims, in short as the basis for evaluative judgments. A philosophical conception of reasonableness serves at least three important functions in argumentative encounters: participants use it to (1) describe, critique and justify the norms regulating the inclusion and exclusion of group perspectives, modes of communication, topics, and knowledge claims in public deliberations; because (2) it functions as a standard by which the practices of public justification can be measured; and (3) it in turns informs the design of processes for both training participants and facilitating public communication.
Reasonableness is a political and moral concept used by participants in the ongoing disputes that characterize life in a pluralistic society. I think that this warrants a the formulation of a public-political conception of reasonableness. One that is grounded in both the empirical details of argumentation as well as in our philosophical reflection. In fact, if what I have been saying is true, these two activities should not be seen as distinct. I now turn to setting out a public/political account of reasonableness as found in the ideal of public reason.

2. The Ideal of Public Reason
The ideal of public reason does not refer to the heightened reasoning powers of the Leviathan. Public reason refers to the common reason, understood as a means of formulating plans, putting ends in order and making decisions accordingly, of the public in its capacity as citizens constituting a polity. Rawls (1989), working from Kant’s (1991/1784) discussion of free public reason, formulates public reason as the standard of reasonableness that ought to govern political discussion in a liberal democracy:
Great values fall under the idea of free public reason and are expressed in the guidelines for public inquiry and in the steps taken to secure that such inquiry is free and public, as well as informed and reasonable. These values include not only the appropriate use of the fundamental concepts of judgment, inference, and evidence, but also the virtues of reasonableness and fair-mindedness as shown to the adherence to the criteria and procedures of common sense knowledge, and to the methods and conclusions of science when not controversial, as well as respect for the precepts governing reasonable political discussion (233-234).
The ideal of public reason is the standard citizens in a pluralistic society hold each other to when advancing arguments about what constitutes the good. It is a standard that demands that citizens be able to explain their political convictions to one another in terms of a reasonable balance of public political values rather than by referring to comprehensive doctrines that may exclude others deepest convictions. That is, when citizens are called on to justify their political convictions and votes in public forums they should be ready to explain the basis for their actions to one another in terms that others could reasonably endorse as “consistent with their freedom and equality” (Rawls, 1993, p. 218). Public reason contrasts with the nonpublic reason of churches, trade unions, neighborhood associations and other institutions constituting civil society. Nonpublic reasoning might include premises about the authority of sacred texts and modes of reasoning that might appeal to the interpretive authority of particular individuals (Solum, 1993). Public reason also contrasts with the technical and instrumental reasoning of corporations, scientific communities and bureaucratic organizations. However, when these institutions address each other and the public at large in public forums they are expected to base their arguments on premises and modes of reasoning comprehensible and reasonably acceptable by all.

Of course, citizens draw their political convictions from their religious beliefs, community membership, occupational identities, and other nonpublic commitments. Moreover, they ought to be free to do so. Yet, given the irreducible plurality of doctrines that define our moral, religious, philosophical, and political convictions, a standard of public reason is necessary to distinguish the legitimate from the coercive use of political power. The exercise of political power is justifiable and hence legitimate only when exercised in a manner that is consistent with the freedom and equality of all citizens. For Rawls (1993), this “liberal principle of legitimacy” imposes a duty of civility-the obligation that citizens, as well as public officials, explain their how the principles and policies, at least those that would affect others, can be supported by the values of public reason (217). The duty of civility and standards of public reason do not apply to personal deliberations or those of voluntary associations. But the ideal of public reason and duty of civility does hold for political advocacy in public forums and to how citizens vote in public elections when fundamental process of government (e.g., the powers of the legislature, the scope of majority rule) or basic liberties (e.g., suffrage, freedom of thought and expression, and the protections of the law) are at stake.

The ideal of public reason is a distinctively political conception of reasonableness. From a political point of view an argument or argumentative practice is reasonable if it meets several conditions (Gaus, 1997). First, it must be consistent with the efforts to achieve and abide by a fair system of cooperation. Second, it must not attempt to repress competing reasonable arguments and doctrines. Third, it must recognize that what Rawls’ terms the “burdens of judgment” will necessarily lead to conflicting judgments about the nature of the good. That is, we must recognize that in our political disputes that the evidence is conflicting and complex, that participants will disagree about the relative weight of relevant facts, that our moral and political concepts are indeterminate and subject to hard cases that engender competing interpretations, that persons will evaluate claims in light of their experience and that experience not only differs among persons but subject to change within any one persons lifetime, and that in persistent public problems force us to select among our cherished values or restrict them in light of the needs and desires of others. Many of our political disputes have no clear or right answer. Therefore, it is unreasonable to put forth arguments which claim that there is a univocal interpretation of the problem and the requirements necessary for it solution. It is also unreasonable to argue for a suspension of a process of reflective and inclusive public debate and discussion for reasons of efficacy. The ideal of public reason advances a standard of reasonableness that is political rather than epistemic. Epistemic conflicts, which are inevitable in a system of free institutions, can be accommodated within the purview of an ideal of public reason. In fact it is this ability to accommodate epistemic conflicts that makes the ideal of public reason a purely politcal standard of reasonableness.

The ideal of public reason, therefore, constitutes a critical standard of reasonableness that participants invoke to regulate their own and each other’s argumentative practices in two ways. First, it regulates the production of arguments by serving as a standard for self-evaluation. Citizens can use the ideal as a guide for determining which of their arguments are acceptable for public discussion. Second, the ideal of public reason regulates the evaluation of argumentation by serving as a standard for political criticism. One can criticize anothers’ arguments on the grounds that by resting on premises and modes of reasoning that can not be warranted by the standards of public reason they transgress the limits of civility. This second role, while not assuming nor justifying enforcement by the coercive use of institutional power, does not rule out the use of social pressure to encourage compliance with the standards of public reason (Solum, 1993, p. 733). By offering acceptable reasons and voicing disapproval of those reasons which transgress the limits of civility citizens can use the ideal of public reason as method of changing one another’s political behavior. Moreover, the procedures of public deliberation not only regulate disagreement but actually constitute citizens that have the capacity and desire to engage in critical discussion. Hence, debate governed by the ideals of public reason, by inculcating a democratic ethos, becomes a form of democratic paideia.
Unlike purely descriptive accounts the ideal of public reason provides an account of reasonableness that is not simply a reflection of current public sentiment. To be sure, many people fail to recognize the distinction between public and nonpublic reasons, nor do they evaluate their own and others arguments according to this standard. Yet, people can, and sometimes do, recognize and accept these distinction in particular cases. The ideal of public reason is a normative standard designed to regulate public discourse. It is a critical standard of reasonableness whose application can be accounted for and critiqued. Therefore, it avoids the relativism of accounts that treat reasonableness as the reflection of a community’s argumentative practices.
Unlike a purely normative account the ideal of public reason recognizes the plurality of reason. It does not presuppose a single standard of reasonableness, but is appropriate for conflicts where multiple philosophical conceptions of the reasonable are invoked and participants must do work to adjudicate between them. Public reason does not aim for the construction of a single norm to govern our political and moral conduct. Rather, when invoking the ideal of public reason as a critical standard of reasonableness we work to create the framework for forging an ongoing reflexive public consensus on how to speak and argue with each other. A political standard of reasonableness, then, permits not denies or avoids the differences engendering the deep conflicts present liberal democracies. A political standard of reasonableness, unlike epistemic conceptions, does not depend on the resolution of a difference of opinion or the acceptance of a conclusion based upon the premises given, but only that citizens continue to cooperate and compromise in public argument. It is precisely this continued cooperation that is at stake in forging a democratic life based on free and critical deliberation.

REFERENCES
Gaus, G. (1997). Reason, justification, and consensus: why democracy can’t have it all. In: J. Bohman & w. Rehg (Eds.), Deliberative Democracy: Essays on Reason and Politics (pp. 205-242, ch. 7). Boston: MIT Press.
Hicks, D. & P. Glenn. (1995). The pragmatics of sexual harassment: two devices for constructing a hostile environment. In: S. Ragan, D. Bystrom. L. Kaid & C. Beck (Eds.), The lynching of Language: Gender, Politics, and Power in the Hill-Thomas
Hearings (pp. 215-238, ch. 11). Urbana: University of Illinois Press.
Kant, I. (1991/1784). An answer to the question: “What is enlightenment?” In: H. Reiss (Ed.), Political Writings (pp. 54-60), Cambridge: Cambridge University Press.
Keating, G. (1996). Reasonableness and rationality in negligence theory. Stanford Law Review, 48, 311-383.
Rawls, J. (1989) The domain of the political and overlapping consensus, New York University Law Review, 64, 233-255.
Rawls, J. (1993). Political Liberalism. New York: Columbia University Press
Siegel, H. & J. Biro. Epistemic normativity, argumentation, and fallacies. Argumentation, 11, 277-292.
Solum, L. (1993). Constructing the ideal of public reason. San Diego Law Review, 30, 729-762.
Taylor, T. (1997) Theorizing Language. Amsterdam: Pergamon.
Unger, R. (1987). Social Theory: Its Situation and Its Tasks. Cambridge: Cambridge University Press.

1. Introduction
Some arguments have premisses which make their conclusions probable. Or so, at least, it seems. But the attempt to understand how and under what circumstances they do so has proved surprisingly difficult. Carnap’s project of an inductive logic (Carnap 1962/1950) foundered on the inability to single out a unique measure function which would assign initial probabilities to each set of structurally isomorphic state descriptions (Carnap & Jeffrey 1971, Jeffrey 1980). On a Bayesian personalist approach, which goes back to F. P. Ramsey’s 1926 paper “Truth and probability” (1990/1926), an initial purely subjective (hence “personal”) assignment of probabilities is modified according to Bayes’ theorem in the light of subsequent evidence (hence “Bayesian”); Bayesian personalism has recently had vigorous defenders (e.g. Howson & Urbach 1989, Kaplan 1996), but a critical examination by John Earman (1992) concluded that it still faces, among other difficulties, the so-called “problem of old evidence” (explaining how old evidence can make a hypothesis more probable, as the already known perturbation in the orbit of the planet Mercury evidently did for Einstein’s general theory of relativity). John L. Pollock has attempted to ground a comprehensive theory of inductive reasoning and inductive argument on what he calls “nomic probability” (Pollock 1990: 25), the kind of objective probability involved in statistical laws of nature. Various authors have developed criteria for “argumentation schemata” covering such types of argument as enumerative induction (particular and general; cf. Russell (1948)), eliminative induction (inference to the best explanation), and so-called “direct inference”; such ad hoc approaches, exemplified by Grennan (1997), often seem plausible, but need justification.
In this paper, I wish to make a start on developing criteria for determining whether the premisses of an argument make its conclusion probable; we could say that such a situation is one in which the premisses “probabilify” the conclusion, so the subject of this paper is probabilification.
I propose to start from Stephen Thomas’ discussion of an example in the 1997 (fourth) edition of his Practical Reasoning in Natural Language (Thomas 1997: 130-131). In his discussion, Thomas maintains a position adopted in print 13 years earlier (Thomas 1984: 32), even though a subsequently published paper (Nolt 1985: 56) rejected that position. It will turn out that, in this dispute, Nolt is correct and Thomas is mistaken. The textbook discussion makes clear, in a way that the earlier paper did not, why Thomas made his mistake. His reason is a seductive one, and exposing its inadequacy has, I shall maintain, some negative lessons for the evaluation of enumerative induction and, more generally, of inferences from confirmatory evidence to the probable truth of any hypothesis under investigation.

2. Thomas’ discussion
Thomas discusses the strength of support given to the conclusion of the following invented argument by its premisses:
1. The fifty marbles in this bag were thoroughly stirred and mixed before sampling.
The first forty-eight marbles examined, each chosen at random, were all clear glass.
Therefore, the remaining two marbles are both clear glass (Thomas 1997: 130).

In its surface form, this argument projects a property of all examined members of a class to two unexamined members of that class. But, since the two marbles in the bag are the only unexamined members of the class, the argument by implication projects the property of being clear glass to all members of the class. Thus, although in its external form it is an example of what is commonly called “particular enumerative induction”, its logic is that of what is usually called “universal enumerative induction” (Russell 1948).
Thomas writes the following about his example: “The large proportion of marbles examined and the fact that the marbles were thoroughly stirred before sampling and were chosen at random, all contribute to the strength of this reasoning. Yet the reasons do not make the truth of the conclusion totally certain. It remains possible that one (or even both) of the two marbles still in the bag is not made of clear glass. Although we can imagine that the reasons are true while the conclusion is false, this situation is unlikely. Consequently, the step from these reasons to the conclusion is rated as strong [emphasis in original – DH]. Unlikely as it may be, the logical possibility that a remaining marble is not clear glass (despite the fact that the first 48 drawn at random were clear glass) makes this step of reasoning less than 100 per cent certain, the highest possible degree of strength.” (Thomas, 1997: 131)
In calling the step from the reasons to the conclusion strong, Thomas is claiming that the reasons if true make the conclusion highly probable, though not certain. As he puts it: “A practical measure of a strong [emphasis in original – DH] degree of support is that the reasons be related to the conclusion in such a way that the truth of the reasons, if they were true, would establish the truth of the conclusion with a degree of certainty strong enough to count on it with confidence for all realistic purposes.” (Thomas 1997: 130)
In the earlier exchange in Informal Logic, Thomas maintained that the probability of the conclusion in a similar example was “well in excess of 80%,” but did not explain how he arrived at such a quantitative estimate (1984:32) (In the earlier example, the premiss was that 49 of 50 marbles in an urn had been examined and found to be blue; the conclusion was that the 50th marble will also be blue.) Nolt replied that “in fact there is no way to calculate such a probability from the information Thomas gives… We can, without violating any mathematical law, assign that proposition [that the next marble to be selected from the urn is blue–DH] any probability we like.” (1985: 56) Perhaps because Nolt gave no argument for his counter-claim, Thomas obviously remained unconvinced.

3. The mistake
Thomas appeals to its being unlikely “that the reasons are true while the conclusion is false” (1997:131). In other words, he regards as unlikely the following situation: 48 marbles selected at random without replacement from this jar containing 50 marbles are clear glass, while one or both of the non-selected marbles is not clear glass. Now we might estimate the value of this probability as follows. If the bag contains 49 clear marbles, this probability is 2/50, or .04.[i] If the bag contains 48 clear marbles, this probability is 1/1225, or .00082.[ii] If we are given only that the bag contains either 48 or 49 clear marbles, then the probability is somewhere between these two values, depending on what relative likelihood we assign to the two possibilities.
Since the probability of a set of mutually exclusive and jointly exhaustive events sums to 1, then by subtraction the probability of the remaining two marbles being clear glass is .96 in the one case and .99918 in the other, or some value in between if we do not know which of the two cases obtains. We might then be inclined to take one of these values, or the range between them, as the likelihood that the conclusion of our argument is true, given that the reasons are true. But this would be a mistake. For the argument corresponding to the probability of .96 (or .99918, or the range between) is the following argument:
2. The fifty marbles in this bag, of which 49 (or 48, or either 48 or 49) were clear glass and the remaining one was not (or two were not), were thoroughly stirred and mixed before sampling. The first forty-eight marbles, each chosen at random, were examined. Therefore, the remaining two marbles are both clear glass.

Although verbally very similar, that is logically a very different argument from (1), the argument whose inference we are evaluating, since it includes in the premiss the assumption that one of the original 50 marbles is not made of clear glass (or two are not) and it does not include the information that the 48 examined marbles are made of clear glass; indeed, this original premiss is incompatible with the combination of the new argument’s premiss and its conclusion. What has gone wrong? In construing as we did the likelihood that the reasons are true while the conclusion is false, we have treated the problem as one of estimating the probability of a given outcome of a not yet completed stochastic (indeterministic) process. But our problem does not involve any such stochastic processes.
We are supposing that the 48 marbles have already been selected, and that they are all clear glass. There is no indeterminacy about their colour, or about the colour of the remaining marbles in the bag. So the probability we are interested in is not a probability in any frequency sense, but an epistemic probability: the degree of confidence in the truth of the conclusion which the truth of the premisses would give to a rational person.
Further, we have confused a conditional probability with the probability of a conjunction. Specifically, we have confused the probability that the conclusion is false, given that the premiss is true, with the probability that the conclusion is false while the premiss is true, where this “while” is construed as a conjunction. Given the standard constraints imposed on a probability function by the Kolmogorov axioms[iii], we can equate the probability that an argument’s conclusion is true, given that its premisses are true, with 1 minus the probability that the conclusion is false, given that its premisses are true. (p(C|P) = 1 – p(not C|P).)[iv] But in general we cannot equate the probability that the conclusion is false, given that its premisses are true, with the probability that the conclusion is false while its premisses are true. (In general, p(not C|P) _ p(not C & P)).
The possibility of such a confusion shows that there is a danger of misapplying Thomas’ general test for assessing the degree of support given to a conclusion by its premisses. Since this general test has been incorporated into other textbooks (e.g. Pinto & Blair 1993; Pinto, Blair & Parr 1993), it is worth noting the need for care in how it is stated. Thomas proposes (1997: 135-136) the following procedure for estimating degree of support.
First, ask whether, supposing the reasons are true, there is any way in which the conclusion nevertheless could be false.
Second, if there are such ways, estimate how likely it is that the most likely of these ways is true; if there are no such ways, the argument is deductively valid.
Third, assess the degree of support of the conclusion by the reasons as the complement of this estimate: strong if the most likely counterexampling way is highly unlikely, moderate if it is unlikely but not highly unlikely, weak if it is only somewhat unlikely, nil if it is at least as likely as not. Care needs to be taken in applying the first of these three steps. One is not looking for a way in which the reasons are true and the conclusion false. One is looking for a way in which, given that the reasons are true, the conclusion is nevertheless false. The difference is subtle but, as the above discussion indicates, important.

4. Some calculations of epistemic probability
We must try, then, to calculate an epistemic conditional probability. It is important to notice that the estimation of such a probability depends not only on the information stated in the premisses, but on other background information at our disposal. For example, we assume that the number of marbles in a bag changes only by removing or adding marbles to the bag; contrast the number of drops of water in a glass, or the number of rabbits in a cage, or the number of mothballs in an open jar. We assume that no marbles left or entered the bag after it had 50 marbles in it, except for the 48 which were examined; in particular, we assume, although the argument does not explicitly say so, that none of the 48 marbles were put back in the bag. We also assume that marbles do not spontaneously change colour on their own; contrast chameleons or mood rings. We cannot ignore this information, since no calculation is possible without making some such assumptions. Such background information plays an even bigger role in more complex real cases. The need to take it into account in estimating the degree of probabilistic support of a hypothesis by evidence is Carnap’s so-called “total evidence requirement” (Carnap 1962/1950: 211-213; cf. Pollock 1990: 133).

We can get some idea of the range of probabilistic support in our example by considering some assumptions which might form part of our additional background information in a real-life situation. I shall consider in turn three cases.
Case 1: Uniformity: The marbles were put in the bag from a single uniform-coloured batch from a production line. (Cf. Hume’s assumption that nature is uniform. In fact, nature is not uniform in all respects, but we often have, or think we have, reason to think that we are dealing with a sortal property of a natural kind, e.g. the solubility of a pure substance in a pure substance.) In this case, the conditional epistemic probability that the conclusion is true is 1, since the premisses together with the background information entail the conclusion. Note that in this case the background information makes it unnecessary to examine more than one marble from the bag, just as in many scientific experiments or systematic observations we do not need to accumulate a large number of instances, just enough to make us confident that our lab technique was good and our measurements were accurate.
Case 2: Independence: The marbles in the bag were selected by a random process from a very large stock of marbles of various colours, the proportion of clear glass marbles in this stock being some known ratio r. (For example, the stock had 10 different colours of marble; each colour was assigned a distinct one-digit number, and a random number table was used to select by number the sequence of colours of the marbles put in the bag.) The stock was large enough that taking 50 clear glass marbles from it would not affect substantially the proportion of clear glass marbles in the remainder of the stock. The observed result is of course highly improbable in this case. But improbable events do happen. And drawing 48 clear glass marbles in succession from the bag does not change the probability, relative to the specified background information, that the remaining two marbles are also clear glass; to think otherwise is to subscribe to a fallacious form of the law of large numbers. So the probability is r that the 49th marble is clear glass, and is also r that the 50th marble is clear glass. Since, given the background information, these two events are independent, the probability of their conjunction is the product of the two probabilities, or r2.
Case 3: The travelling gambler: The marbles were put in the bag by a roving gambler who has read Thomas’ textbook. This nefarious individual goes to college and university campuses where Thomas’ textbook is used, and proposes a sinister betting arrangement to unsuspecting students who have read Thomas’ discussion of example (1). He shows them his bag with 50 marbles, which they can count for themselves (without looking inside the bag). He invites them to draw 48 marbles from the bag. If all 48 marbles are clear glass, he offers them, if they are willing to bet a sizeable sum of money, attractive odds that the remaining two marbles are also clear glass, say 3:1 in his favour. (The students in fact believe the chances are overwhelming that the remaining two marbles are clear glass, so they are happy to give him such favourable odds.) There is always a non-clear marble in the bag. Of course, 24 out of every 25 times the odd marble is drawn among the 48, and there is no bet. But every 25th time the roving gambler cleans up. In this case, the probability of the conclusion being true, given the truth of the premisses, is 0, since the premisses and the background information together entail the falsehood of the conclusion.

These three cases collectively vindicate Nolt’s claim that “we can, without violating any mathematical law, assign that proposition [in his example, the proposition that the remaining ball is blue–DH] any probability we like.” (1985: 56) The additional background information supplied in each case does not alter an antecedently determined epistemic probability. Rather, it supplies enough information to enable a definite probability to be calculated at all. Since the resulting probabilities range from 0 to 1, it seems obvious that, by suitable adjustment of background assumptions, we can indeed assign any probability we like to the proposition that the remaining two marbles in the bag are clear glass, given the information in the premisses of (1). Without more information than that supplied in the premisses, we cannot attach even a qualitative degree of confidence to the conclusion, relative to the premisses.

5. The Bayesian approach
The same result obtains in the three cases if we adopt as the basis of the epistemic probability we are estimating some form of Bayesian personalism, which takes our degree of confidence in a proposition to be a function of the odds we would think it fair to give in a bet that the proposition is true, where the system of such confidence assignments is constrained at least by the probability calculus.[v] If we are absolutely confident in a proposition’s truth, then we would think it fair to give somebody who doubted its truth as high odds as the person wished, e.g. a million to one. If we think it just as likely as not that the proposition is true, then we would think it fair to give odds of 1:1 that the proposition is true. In general, if the odds we think fair to give on the truth of a proposition are x:y, then we have a confidence of x ÷ (x + y) in the truth of the proposition, and vice versa.[vi]
The Bayesian approach allows us to use Bayes’ theorem to calculate the epistemic probability that a hypothesis H is true given certain new evidence E, a probability generally referred to as the posterior probability, provided we are given three other epistemic probabilities, each construed as an assignment of a degree of confidence to a proposition. First, we need the prior probability of the hypothesis, that is, the probability that the hypothesis is true, given our background information independently of the new evidence. (I shall call this “p(H/K)”, where p is the probability function, H is the hypothesis and K is our background information apart from the new evidence.) Second, we need the posterior likelihood, the likelihood of the evidence on the assumption that the hypothesis is true, again assuming the same background information which we have independently of the new evidence. (I shall call this “p(E/H & K)”, where E is the new evidence.) Third, we need the prior likelihood of the evidence, the likelihood that the evidence is true on the assumption of our background information, without assuming the truth of the hypothesis under investigation. (I shall call this “p(E/K)”.) Bayes’ theorem tells us that, if the prior likelihood is not zero, the posterior probability of a hypothesis on new evidence is its prior probability multiplied by the ratio of the posterior likelihood of the evidence to its prior likelihood:
(3) p(H/E & K) = p(H/K) × p(E/H & K) ÷ p(E/K).

The proof of the theorem rests on the definition of a conditional probability p(A/B) as the result of dividing the probability that both A and B obtain by the probability that B obtains, provided that this latter probability is not zero. If one replaces the conditional probabilities in Bayes’ theorem according to this definition, one sees that the theorem is correct, provided that neither the prior probability of the hypothesis nor the prior likelihood of the evidence is zero.
In argument (1), as noted in section 2, the hypothesis can be regarded as the hypothesis that all the marbles are clear glass. Since the evidence of the first 48 marbles drawn being clear glass is a logical consequence of the hypothesis that all 50 marbles are clear glass (given implicit background assumptions such as those mentioned at the beginning of section 4 above), the posterior likelihood of the evidence is 1. Hence, in this case the posterior probability of the hypothesis will simply be the prior probability of the hypothesis divided by the prior likelihood of the evidence.
Case 1: On the uniformity assumption, the prior probability that all the marbles are clear glass is, we may suppose, some value r. The prior likelihood that the first 48 marbles drawn from the bag will be clear glass, given the uniformity assumption but not assuming the truth of the hypothesis, is also r. So the posterior probability is 1.
Case 2: On the independence assumption, the prior likelihood that any marble in the bag will be clear glass is r. Since our assumption makes the colour of each marble drawn independent of the colour of any other marble drawn, the prior probability of the hypothesis that all 50 marbles are clear glass is r50, and the prior likelihood that the first 48 marbles drawn from the bag will be clear glass is r48. Hence the posterior probability of the hypothesis is r50 – 48, or r2.
Case 3: On the travelling gambler assumption, the prior probability that all 50 marbles in the bag are clear glass is 0. Hence, whatever the prior likelihood may be, assuming it is not 0, the posterior probability of the hypothesis is 0.
The fact that Bayesian calculations produce the same results in all three cases as the more informal reasoning in section 4 both vindicates the Bayesian approach and increases our confidence in the informal methods of the previous section; there is, I believe, no vicious circularity in using the coincidence of results from two distinct approaches as evidence boosting our confidence in both of them, provided that neither approach is a logical consequence of the other.

6. An invalid argument schema
A tempting approach to our example is to note that the evidence reported in the premisses rules out all but three hypotheses about the distribution of colours among the 50 marbles in the jar:
1. All 50 marbles are clear glass.
2. 49 marbles are clear glass, and one is not clear glass.
3. 48 marbles are clear glass, and two are not clear glass.
One can then note that the evidence is much more likely to occur on the first hypothesis than on the second and third.
On (1), the evidence is bound to be obtained.
On (2), the likelihood of the evidence is .04, as calculated in note 1 above.
On (3), the likelihood of the evidence is .00082, as calculated in note 2 above.

Since the result we observed was inevitable on the first hypothesis but highly unlikely on each of the only two alternative hypotheses consistent with our evidence, does this result not make it highly probable that the first hypothesis is true, and thus that the last two marbles in the jar are clear glass?
The considerations advanced in the above possible solutions show that this method of reasoning is invalid, that is, that the premises do not necessarily confer a high probability on the conclusion of the argument. A Bayesian explanation of why it is invalid is that it does not take into account the prior probability of the three hypotheses. If our background information gives (1) a very much lower prior probability than (2) or (3), the fact that the evidence is exactly what we would expect on the basis of (1), but highly unlikely given (2) or (3), is not enough to make (1) highly probable.[vii]
Thus, the following argument schema, though plausible, must be rejected as invalid:
4. The observed results rule out all but n mutually exclusive hypotheses.
On one of these hypotheses, the observed results were bound to occur. On any of the others, the observed results were highly improbable. Therefore, probably the first hypothesis is correct.

7. Conclusion
The probability which the premisses of an argument confer on its conclusion is the complement of the probability that the conclusion is false, given that the premises are true. But it is a mistake to identify this conditional probability with the probability of a conjunction, the probability that the premises are true while the conclusion is false. Such identification leads to serious errors in estimating the degree of support of an argument’s conclusion by its premisses. Apparent commission of this mistake in contemporary textbooks shows that one must apply with care the procedure of estimating degree of support as the complement of the likelihood that the conclusion is false, given that the premisses are true.
In an enumerative induction, whether universal or particular, the conditional probability that a property observed in all examined members of a class or kind belongs to all, or to one or more hitherto unexamined, individual members of the class or kind must be assigned in the light of an evaluator’s background information.
Uniformity of the examined instances of a kind with respect to some variable can make it certain, highly probable, improbable or even impossible that all the instances of the kind, or the next examined instance(s), will be similar in that respect, depending on an evaluator’s background information. In some cases the background information does not permit assignment of a definite epistemic probability, or even a rough range of such probabilities, to the conclusion. In general, a hypothesis is not necessarily made highly probable by an observed result which is highly likely on that hypothesis but very unlikely on each of its competitors; the prior probabilities of each of the hypotheses under consideration must also be taken into account. [viii]

NOTES
i. In a sequence of 50 random selections without replacement from a bag containing 49 clear marbles and one non-clear marble, there is an equal chance of the drawing of the non-clear marble occurring at any position in the sequence, namely one out of 50; therefore, this is the probability that the drawing of the non-clear marble will occur last in the sequence, and also the probability that the drawing of the non-clear marble will occur second last. Since these events are mutually exclusive, the probability that one or the other of them will occur is the sum of the probability that each will occur, namely 2/50, or .04. This is the same as the probability that, in a random selection without replacement, the first 48 marbles drawn will be clear glass. The same result follows if, using the general multiplication rule for calculating the probability of a conjunction of events, we multiply the probability of choosing a clear marble on the first draw (49/50), the probability of choosing a clear marble on the second draw given that a clear marble has been chosen on the first draw (48/49), and so on, up to the probability of drawing a clear marble on the 48th draw if 47 clear marbles have been drawn on the first 47 draws (2/3). Here and in other calculations in this paper, I use Kolmogorov’s (1956/1933) axioms of the classical probability calculus. See note 3.
ii. In a sequence of 50 random selections without replacement from a bag containing 48 clear marbles and two non-clear marbles, which we may call “marble A” and “marble B”, there is an equal chance of the drawing of marble A occurring at any position in the sequence, namely one out of 50; therefore, this is the probability that the drawing of the marble A will occur last in the sequence. The probability that the drawing of the marble B will occur second last in the sequence, given that the drawing of marble A occurs last, is one out of 49. By the general multiplication rule, the probability of the conjunction of these events is 1/50 x 1/49, or 1/2450. By similar reasoning, the probability that the drawing of marble A will occur second last in the sequence and the drawing of marble B last is also 1/2450. Since the two conjoint events are mutually exclusive, the probability that one or other of them will occur is the sum of these two probabilities, i.e. 2/2450, or 1/1225, or .00082. This is the same as the probability that, in a random selection without replacement, the first 48 marbles drawn will be clear glass. The same result follows if, using the general multiplication rule for calculating the probability of a conjunction of events, we multiply the probability of choosing a clear marble on the first draw (48/50), the probability of choosing a clear marble on the second draw given that a clear marble has been chosen on the first draw (47/49), and so on, up to the probability of drawing a clear marble on the 48th draw if 47 clear marbles have been drawn on the first 47 draws (1/3).
iii. Kolmogorov (1956/1933: 2) proposed in effect the following axioms for the probability calculus (where p is the probability function and P and Q arbitrary arguments, here construed as propositions, to which this function is applied):
(1) p(P) -> 0.
(2) If P is a tautology, then p(P) = 1.
(3) If P and Q are mutually exclusive, then p(P -> Q) = p(P) + p(Q).
Any function which satisfies these or an equivalent set of axioms is a probability function in Kolmogorov’s sense.
iv. This result depends on the assumption that p(P) Õ 0. Given this assumption, we have that:
1 = p(P)/p(P)
= p[(C or not C) & P]/p(P) [conjoining a tautology]
= p[(C & P) or (not C & P)]/p(P) [distribution of disjunction over conjunction]
= [p(C & P) + p(not C & P)]/p(P) [Kolmogorov axiom]
= p(C & P)/p(P) + p(not C & P)/p(P) [arithmetic]
= p (C|P) + p (not C|P) [definition of conditional probability].
Thus, subtracting from each side, 1 – p(not C|P) = p(C|P). This proof constitutes a justification of Thomas’ (1997) test for degree of support, assuming that degree of support is a probability function conforming to Kolmogorov’s axioms.
v. Recently Kaplan (1996: 16-18) has produced a general proof that our personal degrees of confidence in the propositions we entertainought to conform to the constraints of a probability function, on the basis of some plausible assumptions about the structure of rational preferences, within the context of an oversimplified postulate about basic values. Kaplan’s proof avoids some of the unrealistic assumptions of the more crude “Dutch book” argument first advanced by Ramsey (1990/1926) and found for example in Skyrms (1967). Savage (1972 [1954]) produced a more general proof than Kaplan’s, one which does not involve any constraints on what an agent values. As Kaplan (1996) points out, the probability calculus imposes only weak constraints on our assignment of degrees of confidence to propositions; a comprehensive epistemology would impose additional constraints.
vi. The complications in developing this idea are that an agent’s value system does not simply equate value with money and that an agent may have an aversion to, or a liking for, gambling which would distort the effect of their degree of confidence in a proposition.
vii. One may appreciate this fact more readily if one expands the prior likelihood p(E/K) in Bayes’ theorem, using the probability calculus, to get: [p(E/H & K) x p(H/K)] + [p(E/~H & K) x (1 – p(H/K))]. Suppose the evidence E is highly likely if the hypothesis is true but highly unlikely if the hypothesis is false. For example, let p(E/H & K) = 1 and p(E/~H & K) = .0008. Now suppose that the prior probability of the hypothesis is very low; for example, let p(H/K) = .0001. Then p(H/E & K) = p(H/K) x p(E/H & K) x {[p(E/H & K) x p(H/K)] + [p(E/~H & K) x (1 – p(H/K))]\} = .0001 x 1 x {[1 x .0001] + [.0008 x (1 -.0001)] = .0001 x {.0001 + [.0008 x .9999]\} = .0001 \’f7 \{.0001 + .0008\} = .0001 x .0009 = 1/9 = .1111. So, even though the evidence is bound to occur if the hypothesis is true and highly unlikely if the hypothesis is false, the posterior probability of the hypothesis, given the evidence, is only .1111.
viii. For their comments on earlier drafts of this paper, I would like to thank Howard Simmons, Roderic Girle, Francisca Snoeck Henkemans, Sally Jackson, Robert H. Ennis, two anonymous referees for the Canadian Philosophical Association, and above all Robert C. Pinto, who produced a challenging commentary when I presented an earlier version of this paper at the University of Windsor, and who saved me from some embarrassing technical errors. The aforementioned discussants are of course not responsible for any flaws that remain.

REFERENCES
Carnap, Rudolf (1962/1950). Logical Foundations of Probability, second edition. Chicago: University of Chicago Press.
Carnap, Rudolf & Richard C. Jeffrey (Eds.) (1971). Studies in Inductive Logic and Probability, Volume I. Berkeley, Los Angeles and London: University of California Press.
Earman, John. Bayes or Bust?: A Critical Examination of Bayesian Confirmation Theory. Cambridge, MA: MIT Press.
Grennan, Wayne (1997). Informal Logic: Issues and Techniques. Montreal: McGill-Queen’s University Press.
Howson, Colin & Peter Urbach (1989). Scientific Reasoning: The Bayesian Approach. La Salle, IL: Open Court.
Jeffrey, Richard C. (Ed.) (1980). Studies in Inductive Logic and Probability, Volume II. Berkeley, Los Angeles and London: University of California Press.
Kaplan, Mark (1996). Decision Theory as Philosophy. Cambridge: Cambridge University Press.
Kolmogorov, A. N. (1956/1933). Foundations of the Theory of Probability, second English edition, translated and edited by Nathan Morrison. New York: Chelsea.
Nolt, John (1985). More on induction and possible worlds: replies to Thomas and Kahane. Informal Logic 7, 1, 55-60.
Pinto, Robert C. & J. Anthony Blair (1993). Reasoning: A Practical Guide. Englewood Cliffs, NJ: Prentice-Hall.
Pinto, Robert C., J. Anthony Blair & Katharine E. Parr (1993). Reasoning: A Practical Guide for Canadian Students. Scarborough, ON: Prentice-Hall.
Pollock, John L. (1990). Nomic Probability and the Foundations of Induction. New York and Oxford: Oxford University Press.
Ramsey, F. P. (1990/1926). Truth and probability. In: D. H. Mellor (Ed.), Philosophical Papers (pp. 52-94, Ch. 4), Cambridge: Cambridge University Press.
Russell, Bertrand. (1948). Human Knowledge: Its Scope and Limits. New York: Simon and Schuster.
Savage, Leonard J. (1972/1954). The Foundations of Statistics, second revised edition. New York: Dover.
Skyrms, Brian (1967). Choice and Chance: An Introduction to Inductive Logic. Belmont, CA: Dickenson.
Thomas, Stephen N. (1984). Degrees of validity and ratios of conceivable worlds. Informal Logic 6, 3: 31-34.
Thomas, Stephen N. (1997/1986/1981/1973). Practical Reasoning in Natural Language, 4th edition. Upper Saddle River, NJ: Prentice-Hall.

1. Introduction
The following fragment has been taken from an argumentative essay in Italian, written by a native Dutch university student of Italian. The essay argues that even in a unified Europe, the single European countries will not loose their national identity.

(1) Unificazione europea: perdita dell’identità nazionale?
Non penso che l’unificazione di Europa sarà una perdità dell’identità nazionale (Opinion 1). Secondo me Europa è formato di molto paesi che hanno tutto i propri valori e le proprie tradizione. Questi valori e tradizione sono formati per molti secoli e non camberanno di colpo (Argument 1). Certo, ci sarà uno scambio dei valori e delle tradizione tra i paesi (Counterargument 1 rejected) ma penso che questo scambio sarà utile per arricchere la propria cultura (Argument 2). Ci sono anche le lingue che sono molto diverse (Argument 3). L’inglese sarà la lingua principale (Counterargument 2 rejected), ma penso che non sia possibile (Qualifier 1) di trasformare tutte le lingue nell’inglese (Argument 4). Per me l’unificazione vuol dire che Europa sia un insieme di paesi separati con un zielo uguale: la collaborazione sul campo economico e politico (Conclusion 1).

(European unification: a loss of national identity?)
I don’t think the unification of Europe will lead to a loss of national identity (Opinion 1). In my opinion Europe consists of many countries and each of them has its own values and traditions. These values and traditions have developed over many centuries and will not change all of a sudden (Argument 1). Of course, there will be an exchange of values and traditions between countries (Counterargument 1 rejected), but I think this exchange will be useful and will enrich each country’s culture (Argument 2). Also the languages are very different (Argument 3). English will be the main language (Counterargument 2 rejected), but I think it will be impossible to transform all languages into English (Argument 4). For me unification means that Europe will be a mixture of separate countries with one common goal: collabaration in the fields of economy and politics (Conclusion 1).][i]
To defend his point of view, introduced by standpoint markers like I think, I don’t think, in my opinion, for me, the writer puts forward four arguments. The text also contains a qualifier to mark the degree of certainty with which he regards his standpoint, a conclusion and two counterarguments, which are rejected by the writer. There are only few connectives or argumentative indicators, such as because and consequently. Figures of speech such as metaphors and rhetorical questions are absent. In spite of several language errors, the argumentation is nonetheless adequate.
Producing written argumentative discourse in a foreign or a second language (L2) is a fairly demanding task. L2 writers have to acquire a number of lexical and syntactic devices to enable them to use the argumentative categories that are included in the macro-argumentative structure. The argumentative function of an utterance can be marked linguistically by means of argumentative indicators or by other lexical and syntactic devices (verbal constructions, morpho-syntactic marking, communicative formulas, performatives), which L2 writers must be able to handle. They must also be acquainted with L2 pragma-rhetorical and stylistic conventions.

These are largely language specific and relate to the types of arguments that can be used, the sequence of these arguments, the choice of register, the psychological distance between writer and reader, and the use of modality markers and figures of speech.
Although L2 writers are likely to transfer to L2 a large number of the cognitive, metacognitive and argumentative skills acquired in their mother tongue (L1), the argumentation structure of their texts may be negatively affected by linguistic deficiencies in their L2 knowledge and by their lack of knowledge of the pragma-rhetorical and stylistic patterns of L2. As a result, the argumentative essays in L2 and L1 may differ in complexity and in the occurrence of different argumentative categories. The same may be true for the use of argumentative indicators, modality markers and other lexical and syntactic devices. There may also be differences in the use of figures of speech and other pragma-rhetorical devices.

2. Research questions and experiment
In this article some of the results are discussed of a comparative study of the linguistic and pragma-rhetorical characteristics of argumentative discourse in Italian as a second language and Dutch as a first language. The following research questions are addressed:
1. To what extent does the macro-argumentative structure in L2 differ from L1, with regard to the occurrence of obligatory and optional argumentative categories and subcategories and the use of hypotactical versus paratactical structures of argumentation?
2. What differences can be observed between L2 and L1 concerning the use of argumentative indicators and other lexical and syntactic devices employed by the writers for the marking of obligatory and optional argumentative categories and subcategories?
3. What is the role in L2 and L1 of pragma-rhetorical devices with an indirect argumentative function, such as metaphors and rhetorical questions?

The experiment on which the study was based, was carried out among a group of 85 university students at the University of Amsterdam. The subjects were all in their third year. Their language proficiency in Italian ranged from lower-intermediate to upper-intermediate. The participants were asked to write two argumentative essays, one in Italian and one in Dutch. On the basis of global scoring by three independent judges, the L2 essays were grouped intro three proficiency levels (level 1, 2 and 3). 15 essays of each proficiency level were selected for the analysis of the argumentation structure. To gain a better insight into the use of argumentative indicators and pragma-rhetorical devices in native Italian in comparison with L2 Italian, the essays written by a group of 45 native Italian exchange students at the University of Amsterdam were also analyzed.

3. Language independent and language dependent  skills
Writing argumentative prose presupposes a number of cognitive operations: Identification and Differentation (a writer points to the existence of something by designating it), Stabilization and Destabilization (the writer chooses to speak of this rather than that), Appropriation and Relinquishing (the degree to which the writer identifies with something; this may include all possible degrees of conviction, belief, certainty or prudence (Vignaux 1991). Apart from these cognitive operations, writers make use of metacognitive skills connected with the writing process. In the well-known process models of writing by Flower and Hayes (1981) and Bereiter and Scardamalia (1987) several metacognitive components of the writing process are distinguished, such as planning, monitoring, evaluation, generation and selection of content and transformation and coding of thoughts into written language.
A number of specific argumentation skills are also required. Taking into account the type of reader he is going to write for, the writer of an argumentative text has to make clear his positive or negative commitment to a point of view. This point of view has to be supported not only by good arguments, but also by possible counterarguments or rebuttals. Once the arguments and counterarguments have been found, the argumentation structure has to be drawn up and the internal organization of the single arguments (the argumentation scheme) has to be established. The argumentation structure can be simple or more complex, depending on how the writer organizes the defence of his standpoint and relates it to doubts and criticisms. The argumentation scheme characterizes the type of justification provided for the standpoint (Garssen 1997; Van Eemeren, Grootendorst & Snoeck Henkemans 1996: 16-19).
The cognitive, metacognitive and argumentation skills acquired in L1 are language independent. They constitute the basis of a learner’s L2 argumentative competence as well. In addition, L2 argumentative competence consists of L2 pragma-rethorical and linguistic skills. These skills are largely language specific and have to be acquired specially for L2. In the acquisition of the lexical, syntactic and pragma-rhetorical devices required for the production of argumentative discourse and in the use of argumentative indicators linguistic and pragma-rhetorical transfer from L1 to L2 may occur (Odlin 1989; Kasper 1992; Kasper & Schmidt 1996). L1 transfer doesn’t necessary lead to errors, because parallelism of L1 and L2 may also be a facilitating factor. Transfer may also result in learners overusing argumentative indicators and pragma-rhetorical devices with an L1 equivalent and underusing others without an L1 equivalent.

One might wonder whether L2 argumentation is mainly a question of good argumentation skills based on argumentation skills acquired in L1, or of good L2 knowledge. According to the so-called Linguistic Threshold Hypothesis (Alderson 1984; Clarke 1979; Cziko 1980), the cognitive, metacognitive and pragma-rhetorical L1 skills will only become operative in L2, if the L2 knowledge has passed a particular threshold level of linguistic competence. It is shown by a number of studies in the field of reading and writing in L1 and L2 (Bernhardt & Kamil 1995; Cumming 1989, 1995; Schoonen, Hulstijn & Bossers 1998) that, although L1 argumentative competence considered as a specific form of meta-cognition affects L2 writing, L2 knowledge is probably the major predictor of L2 text quality. On the basis of this research the following assumptions underlying the present study may be put forward:
1. Metacognitive knowledge about argumentation and the writing process in general, based on L1 knowledge, may be a significant factor, but L2 knowledge is the best predictor of L2 argumentation.
2. L1 based knowledge of argumentation skills cannot compensate for a lack of L2 knowledge.
3. If the L2 knowledge remains below a certain threshold or linguistic minimum, L2 learners are unable to utilize the argumentation skills acquired in L1.

4. Categories of argumentation
The study of argumentation has so far not resulted in a generally accepted theoretical model, but is characterized by the coexistence of several approaches and theoretical models. Van Eemeren and Grootendorst’s well known pragma-dialectical model (1984; 1992; 1994), being the theoretical background of any pragmatically orientated analysis of argumentation, constituted the general point of departure for the present study. For the investigation of the linguistic and pragma-rhetorical characteristics of the argumentation structure in L2 and L1 the argumentative grammar proposed by Lo Cascio (1991a; 1991b; 1995) was used. Lo Cascio’s model has the advantage of combining a logico-semantic and pragmatic analysis with a syntactic-linguistic analysis. Furthermore it takes into account the recursive, hierarchical nature of argumentation.
Lo Cascio, expanding Toulmin’s procedure for defending claims (1958/1964), distinguishes eight argumentative categories, three of which are obligatory and five optional. The obligatory categories are Opinion and Conclusion (O; C); Argument and Counterargument (A; CA) and General Rule (GR), Toulmin’s Warrant which allows that the Argument can be considered a good support for the Opinion (1a-1c). The optional categories are subdivided into adjuncts and specifiers. The adjuncts are Rebuttal (REBUT), Reinforcement (REINF) and Alternative (AL); the specifiers are Qualifier (Q) and Backing (B). Both Reinforcement (although, in spite of), Rebuttal (unless) and Alternative (nevertheless) have a counterargumentative function and, although with different counterargumentative force, call into question the validity of the Opinion by presenting alternative arguments, conclusions or counterexamples. Reinforcement can be realized both by a hypotactical and a paratactical linguistic structure (1c-1d). The Qualifier or modal element (probably, perhaps) and the Backing (according to, as stated by) have a specifying function and are expansions of the obligatory argumentative categories. They may strengthen or weaken the illocutionary force of the category they belong to (1g-1h).
For the benefit of the present analysis two argumentative subcategories were added to Lo Cascio’s model: Condition (COND) and Precisizer (PRECIS). Condition (on condition that, providing) and Precisizer (at least) may also influence the illocutionary force of the utterance, by restricting or circumscribing the scope of the category they belong to -often the Opinion or the Argument- and by putting forward the conditions under which an Opinion or an Argument will hold (1i-1j).

Obligatory categories
(1a) I don’t think he’s a very kind person (O)
(1b) This book is not very interesting (O), since it does not contain any new facts (A), so don’t buy it (C), because buying books which do not give any new information usually doesn’t make sense (GR).

Optional categories
Adjuncts
(1c) He will pass the examination (O), although he has been ill (REINF, hypotac).
(1d) He has been ill (REINF, paratac) but he will pass the examination (O).
(1e) Unless the weather is too bad (REBUT), I think (Q) she will go for a walk (O).
(1f) I’m not rich (O), nevertheless (AL) I can’t complain. Specifiers
(1g) He is likely (Q) to come this afternoon (O).
(1h) According to the newspapers (B), the President will visit Japan in January.

Subcategories
(1i) She will probably (Q) lend you her car, provided you drive carefully (COND).
(1j) I guess it takes about six hours to get there, at least that’s what he told me (PRECIS).

4. Accessibility and linguistic and pragma-rhetorical realization of L2 argumentative categories
4.1. Accessibility
One of the basic assumptions of this study is that the accessibility of the obligatory and optional argumentative categories and subcategories in L2 is determined by mutual implicational relations and by inherent cognitive complexity, communicative necessity, pragma-rhetorical complexity and linguistic complexity, as shown by Figure 1. Together these constraints function as a filter which may in some degree delay access to the categories in L2.[ii] Also the acquisition of argumentative discourse by young L1 speakers is probably constrained by these factors, but their nature and weight in L1 is likely to be quite different from their influence in L2.[iii]
With regard to implicationality it may be hypothesized that the presence of the optional categories and subcategories implies the presence of the obligatory categories, while the opposite is not the case. As for cognitive complexity the optional and obligatory categories are likely to be more complex than the obligatory categories, but their communicative necessity is probably less important. Concerning pragma-rhetorical complexity there is probably not much difference between the obligatory and non-obligatory categories: the use of specific L2 pragma-rhetorical devices will be difficult for any category. Linguistically the optional categories are probably more complex, due to the inherent complexity of the linguistic structures required for their realization. Linguistic complexity is also influenced by certain linguistic properties of the target language, such as markedness, input frequency, transparency, form-function relationship, semantic unequivocality and syntheticity (see Figure 1).[iv]

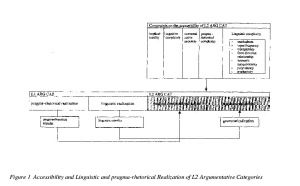
Figure 1 Accessibility and Linguistic and pragma-rhetorical Realization of L2 Argumentative Categories

As a result of implicationality, cognitive complexity, communicative necessity, pragma-rhetorical complexity and linguistic complexity, it may be be expected that the optional categories and subcategories will be used later in L2 production than the obligatory categories. Furthermore we may assume that less proficient L2 writers will presumably resort to linguistic  simplification and reduction. This may affect the textual organization and lead to a preference for the use of syntactically coordinate argumentative categories, rather than syntactically subordinate categories. Another effect may be that the macro-argumentative structure in L2 is less hypotactically organized than its L1 equivalent. Proficient writers will be able to take advantage of their argumentative L1 skills. A further increase in L2 knowledge is likely to affect L2 text positively, but will not further increase the complexity of the macro-argumentative structure of the L2 texts.

4.2 Grammaticalization
A second assumption underlying the present study is that acquisition of the linguistic marking devices of L2 argumentative categories can be considered as a process of increasing grammaticalization (Figure 1). As a consequence, with regard to the linguistic realization of the argumentative categories L2 and L1 may differ in the degree of grammaticalization (cfr. Giacalone Ramat 1992; 1993; 1995; Skiba & Ditmar 1992).
As postulated by this grammaticalization theory, with regard to the acquisition of modality in L2 a first implicit pragmatic phase can be discerned in which all linguistic encoding is lacking and the modal meaning of the utterance has to be inferred from the direct verbal and non-verbal context (2a). In the second, lexical phase modality is realized with simple non-grammaticalized means, such as unmarked adverbs, performative and predicative constructions (2b). Only in the third, grammaticalized phase are some morpho-syntactic marking devices used, such as epistemic use of future tense and modal verbs, conditional and subjunctive mood, (2c).[v]

(2a)
– Che lavoro ti piacerebbe fare?
– A me piace come prima, come mio lavoro tecnica di laboratorio, interprete di medico, far questo lavoro a me piace molto, però
pazienza adesso.
[– What kind of work would you like to do?
– To me likes as before, as my work technician of laboratory interpreter for a doctor, to do this work to me liks much, but patience now.]
(2b)
– Cosa farai l’ultimo dell’anno?
– Io pensare così, prima lavorare, quando finisce lavoro sera no?, già tardi, forsa io va al ristorante mio parenti mangiare un po’ no, poi quando finisce tutti clienti imparare danza, fare così.
[– What will you be doing for New Year’s Eve?
– I think so, first work, when ends work evening already late, perhaps I go to restaurant my relatives eat a bit, then when finish all clients learn dance, do so.]
(2c)
– E questo monaco chi potrebbe essere?
– Il monaco dev‘essere un parente della famiglia.
[– And this monk who could he be?
– The munk must be a relative of the family.]

On the basis of grammaticalization we may hypothesize that L2 writers will make use of grammatically and lexically simpler structures than they do in L1. A second consequence is that L2 will contain more argumentative indicators and fewer other lexical and syntactic marking devices than L1, since linguistic realization by means of the latter will probably be more demanding than realization by an unmarked argumentative indicator (3a-3b).
(3a)
Italy in 1945 was little changed, outside of its major cities, since the time of Garibaldi and Cavour, because it was still predominantly a peasant country, of great and unspoiled natural beauty, of sleeping provincial cities, of enduring poverty, especially in the South.
(3b)
Italy in 1945 was little changed, outside of its major cities, since the time of Garibaldi and Cavour, being still predominantly a peasant country, of great and unspoiled natural beauty, of sleeping provincial cities, of enduring poverty, especially in the South.

4.3 Pragma-rhetorical devices and figures of speech
Finally it is assumed that pragma-rhetorical realization of L2 argumentative categories is complex for both the obligatory categories and the optional categories and subcategories, as stated in 4.1. The use of pragma-rhetorical devices and figures of speech with an indirect argumentative function, such as metaphors and rhetorical questions which may increase the illocutionary force of the argument is probably closely linked to cognitive and psychological factors, since one’s way of writing is part of one’s personality and reflects one’s perception of reality. L2 writers will therefore acquire these pragma-rhetorical devices only at a relatively late stage of the L2 acquisition process. Consequently, these indirectly argumentative devices are likely to play a minor role in the texts of intermediate L2 writers. Moreover, we may suppose that L2 production will be affected in some degree by the pragma-rhetorical and stylistic patterns and conventions of the mother tongue (Figure 1).

5. Results
In this section the results of the analysis of the occurrence of argumentative categories, the characteristics of the macro-argumentative structure and the use of argumentative indicators and other marking devices in L2 and L1 are presented and discussed.[vi]

5.1. Argumentative categories in L2 and L1
Table 2 reports the mean number of occurrences in L2 and L1 of the obligatory and optional argumentative categories and subcategories together with the level of significance of the differences between both languages.[vii]

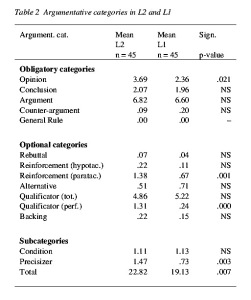
Table 2 – Argumentative categories in L2 and L

Table 2 shows that with regard to the occurrence of the argumentative categories, very few significant differences between L2 and L1 can be observed. The number of Opinions in L2 is larger than that in L1. From this finding we cannot infer, though, that the L2 texts contain more unsubstantiated Opinions, since a comparison of the numerical relation between Opinion and Argument in L2 and L1 shows that this difference is statistically not significant.
In L2 Reinforcement is realized more often as a co-ordinate (Reinforcement paratac.). Similarly, significantly more performatives are used by the writers to express modality (Qualificator perf.). Since performative constructions can be considered as simple non-grammatical modal devices, it might be concluded that linguistic simplification strategies apparently play a more important role in L2. However, there is no significant difference between L2 and L1 with regard to the total number of modal markers (Qualificator tot), nor to the cases in which Reinforcement is realized as a subordinate (Reinforcement hypotac.). Neither are there signs of linguistic simplification in L2 with respect to the Precisizer, since contrary to expectations, the subcategory Precisizer turns out to be more frequent in L2 than in L1.
Another difference between L2 and L1 is that the total number of argumentative components in L2 is significantly higher than in L1. A possible explanation is that L2 writers are more inclined to use simpler lexical and syntactic devices, because their linguistic and pragma-rhetorical tools are less elaborate.

The results show that, on the whole, there are only few differences in the occurrence of obligatory and optional categories and subcategories between L2 and L1. The assumption that the optional categories are used less in L2 than in L1, must therefore be rejected and evidence supporting the hypothesized effect of implicationality, cognitive complexity, communicative necessity, pragma-rhetorical complexity and linguistic complexity cannot be found.

Neither with regard to other characteristics of the macro-argumentative structure such as the use of hypotactic argumentation structures and the occurrence of subordinated argumentative constituents significant differences between L2 and L1 can be detected. This is also true for the number of general opinions and conclusions that are explicitly included in the texts and in the occurrence or absence of introductory non-argumentative text components.

5.2 Linguistic realization of argumentative categories in L2 and L1
A number of differences between the L2 and the L1 essays were found in the degree of grammaticalization and lexical complexity of the linguistic realization of the argumentative categories. Apart from performatives, L2 learners also use a larger number of simple predicative constructions and unmarked adverbs to express modality, such as è possibile, forse (it’s possible, maybe).
Syntactically simplified realizations of Reinforcement as Reinforcement paratac prove to be more frequent in L2 as well. Some differences in morphosyntactic complexity were detected in the realization of Condition, for instance in the use of tenses and verbal modes and in the use of conditional clauses. However, this does not apply to the use of other argumentative categories in L2 and L1, where no differences in the degree of grammaticalization were found.
As predicted by the grammaticalization theory, the total number of argumentative indicators in L2 turns out to be much higher than in L1. Nonetheless, the higher frequency of indicators in the L2 texts is not accompanied by a lower frequency of other lexical and syntactic marking devices, since these are also used more often in L2 (Table 3).

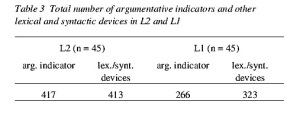
Table 3 – Total number of argumentative indicators and other lexical and syntactic devices in L2 and L1

In both L2 and L1 the learners show a preference for unmarked, colloquial, semantically unequivocal, polyvalent indicators with an easily identifiable equivalent in the mother tongue and a transparant relationship between form and function (ma, però; but, however). Input frequency and syntheticity seem to be less important. L1 influence manifests itself mainly in that indicators with no L1 equivalent are avoided in L2. Where they are not avoided, the syntactic and semantic domain of the indicators is often restricted, for instance in the case of infatti (as a matter of fact), used in L2 Italian only with affirmative and not with argumentative value, or the gerund (parlando, camminando; speaking, walking), reduced to the hypothetical type.[viii]

5.3 Pragma-rhetorical realization
Concerning the textual organization in L2 and L1 also the essays written by the native writers of Italian were analyzed. The comparison of L2 Italian, L1 Dutch and L1 Italian shows that the differences between L2 Italian and L1 Dutch are rather small, while the differences with regard to L1 Italian are numerous. The use of metaphors and rhetorical questions appears to be similar in L2 Italian and L1 Dutch, but fundamentally different in L1 Italian. Newly created metaphors only occur in L1-Italian. In L2 Italian and in Dutch they are completely absent. Similarly, lexicalized, standardized metaphors are used much more frequently in native Italian than in L2 Italian or in Dutch (Table 4). The same is true for the number of indirectly argumentative rhetorical questions (Table 5). As a consequence, evidence for the hypothesis that L2 writers make greater use of this type of

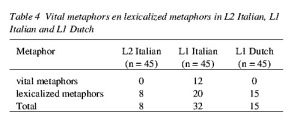
Table 4 – Vital metaphors en lexicalized metaphors in L2 Italian, L1 Italian and L1 Dutch

pragma-rhetorical devices in L2 than they do in their mother tongue was not found. On the other hand, the assumption that the use of pragma-rhetorical devices in L2 is both quantitatively and qualitatively determined by their role in L1, is confirmed by the data.

Both L2 Italian and L1 Dutch are characterized by juxtaposition and by the use of paratactical, asyndetic connections, few punctuation markers and a relatively small number of unmarked colloquial indicators. This is also true for L1 Italian. However, on average the sentences in the native Italian essays are much longer than in L2 Italian and in L1 Dutch, as shown by Table 6.

The considerably higher mean length of the sentences in native Italian does not seem to be caused by syntactic factors, but is probably due to pragma-rhetorical and stylistic factors, such as the accumulation of modal nouns and adjectives, and a large number of enumerations. Generally speaking, the native Italian texts display a greater lexical variety than the Dutch essays. The higher  number of modality markers used by the writers in the Italian L1 texts also gives the impression of greater emotional involvement, as shown by the examples 4a and 4b.

Table 5 – Rhetorical questions in L2 Italian, L1 Italian and L1 Dutch

(4a) L2 Italian
La domanda che l’Italia ha perso il suo fascino, ha due lati. Si può dire di sì, perché ci sono molto scippi, c’è sporco, i monumenti sono spesso in restauro e i musei sono chiusi. Anch’io ho avuto questo esperienza. Al ultimo giorno delle mie vacanze volevo visitare l’Arena di Verona. E era chiusa. Volevo ammirare le statue che sono accanto agli Uffizi a Firenze (ho dimenticato il suo nome) ma potevo vedere solo le impalcature. Non mi piaceva molto a questo momento. Le campeggi sono spesso sporchi, non c’è l’acqua potabile. C’è solo il vicino che ti spia tutto il giorno. Tutto questo sciupa il mio buon umore per un’ora o due, ma dopo, non è più possibile. Perché, dall’altra parte c’è sempre il sole, ci restano molte belle cose da vedere, le piatte deliziose, il paesaggio si bello, gli edifici medievale che emanano una sfera di una tutta altra vita. La gente sulle strade che hanno un buon umore, si ride, si parla, si vive! […]

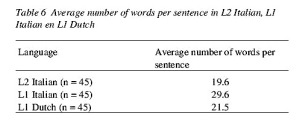
Table 6 – Average number of words per sentence in L2 Italian, L1 Italian en L1 Dutch

[The question of whether Italy has lost its fascination, has two sides. It could be said that Italy has lost it, because there are many pick-pockets, it’s dirty, the tourist sights are under repair and the museums closed. I had the same experience. On the last day of my holiday in Verona I wanted to visit the Arena. It was closed. I wanted to admire the statues near to the Uffizi Galllery in Florence (I forget the name), but the only thing I saw was scaffolding. I wasn’t very pleased at the time. The camp sites are often dirty, there is no drinking water. There is only your neighbour spying on you the whole day. All these things put me in a bad mood for an hour or two, but afterwards, that’s no longer possible. Because, on the other hand, there is always the sun, there are many beautiful things to see, delicious food, a beautiful scenery, medieval buildings suggesting a completely different way of life. People on the street, everybody in a good humour, laughing, talking, just being alive! […]].

(4b) L1 Italian
[…] E quando troppi occhi o mani si impossessano della bellezza, questa si sciupa, diventa piú opaca, perché a portata di tutti. Ma per chi sa apprezzare dal di dentro il mistero dei suoi vicoli, la sgargiata vividezza del suo sole, il vocio di un mercato popolare, i suoi dialetti, l’Italia resta una terra da amare. Una terra non è marcata dai suoi uomini politici, inetti da molti secoli, ma dalle sue masse popolari, dalla loro forza di adattamento, dalla loro volontà di dare a tutti gli aspetti della vita quotidiana quel tocco di gioia di vivere che è indispensabile per la sopravvivenza dell’individuo e del gruppo in qualsiasi società […]. Il mio lungo soggiorno all’estero, in un mondo fatto di interni di casa, di salde amicizie e non di amicizie frettolose come si legano in Italia, mi fa sempre piú ammirare la mia terra e conservarne un ricordo indelibile, come del primo amore vissuto nei primi calori primaverili. Decisamente, l’Italia non ha perso il suo fascino per me.

[[…] And when too many eyes and hands take possession of beauty, it gets spoiled and becomes more opaque, because it has come within everbody’s reach. But for those who are able to appreciate from the inside the mystery of the back streets, the exhuberant vivacity of the sun, the sounds and voices of a local market, the dialects, Italy is still a country to love. A country is not characterized by its politicians, who have been worthless for many centuries already, but by the masses, people with great adaptability, with a will to give to every aspect of daily life that touch of joyfulnes, indispensable for the survival of the individual and the group in any society […]. My long stay abroad, in a world of interiors of houses, of staunch friendships instead of superficial friendships like the ones in Italy, has made me admire my country more and more and I keep an enduring memory of it, like a first love, in the first warmth of spring. For me Italy has certainly not lost its fascination.]

6. Discussion
The study makes clear that there are very few substantial differences between L2 and L1 in the complexity of the argument and the occurrence of the various argumentative categories. Supporting evidence for the hypothesized order in which the argumentative categories are used in L2 production was not found. Future research should make clear to what extent this similarity between L2 and L1 should be attributed to the degree of L2 proficiency of the writers and to the relative proximity of the proficiency levels 1, 2 and 3. The intermediate L2 writers may already have passed the threshold level of linguistic competence required for the use of the L2 argumentative categories. Further research should attempt to establish whether the influence of implicationality, cognitive complexity, communicative necessity, pragma-rhetorical complexity and linguistic complexity can be detected in texts written by beginners and whether there are other factors which may affect the accessibility of the L2 argumentative categories.
The study also shows various grounds for rejecting the grammaticalization theory in its present form. Further research should establish whether particular aspects of the grammaticalization theory might nonetheless be useful in the description of the acquisition of the L2 lexical and syntactic marking devices. The study also makes clear that the majority of differences between L2 and L1 writers resides in the control and manipulation of textual and pragma-rhetorical rather than grammatical strategies. Also the sharp distinction made by Giacalone Ramat et al. between lexicon and syntaxis proves to be theoretically and practically untenable. For these reasons a third, textual phase should perhaps be proposed, rather than a separate grammaticalized phase as postulated by the grammaticalization theory. The linguistic acquisition of the L2 argumentative categories could then be described in terms of a process which starts at the pragmatic level and leads via the lexical-syntactic level to the textual level.
Finally, the study shows that the non-native character of the writing of intermediate L2 writers results in the first place from deviant pragma-rhetorical realizations of the argumentative categories. The type of linguistic realizations plays a relatively minor part. Further research should therefore focus first of all on these pragma-rhetorical realizations and the linguistic and pragma-rhetorical devices which writers have at their disposal to manipulate the emotional involvement of the reader, and secondly on the extent to which differences between L2 and L1 in lexical variety and the choice of modality markers are determined by the contrasting pragma-rhetorical conventions of L2 and L1.

NOTES
[i] The English translations are as close as possible to the Italian originals. The English may therefore sometimes be clumsy.
[ii]Cfr. Keenan and Comrie’s Accessibility Hierarchy (1977).
[iii] Cfr. Keenan and Comrie’s Accessibility Hierarchy (1977).
[iv] For a detailed discussion of these target language features see Vedder (1998).
[v] See for the examples 2a-2c Giacalone Ramat (1992: 310-311; 313; 315).
[vi] As for the occurrence of argumentative categories, the Italian and Dutch essays were compared statistically by means of a t-test and a Wilcoxon-test; possible group effects were measured by a multiple range test (Student-Newman-Keuls post hoc test).
[vii] The symbol n indicates the number of participants, while p – value stands for the degree of probability.
[viii] The following eight types of gerunds can be distinguished in native Italian: temporal; hypothetical, coordinate-narrative; coordinate-evaluative; hypothetical, instrumental; predicative and concessive (Lonzi: 1991: 483-570).

REFERENCES
Alderson, J.C. (1984). Reading in a foreign language: a reading problem or a language problem? In: J.C. Alderson & A.H. Urquhart (eds.), Reading in a foreign language. London: Longman, 1-14.
Bereiter, C. & M. Scardamalia (1987). The psychology of written composition. Hillsdale, NJ/London: Lawrence Erlbaum Associates.
Bernhardt, E.B. & M.L. Kamil (1995). Interpreting relationships between L1 and L2 reading: Consolidating the Linguistic Threshold and the Linguistic Interdependence Hypotheses. Applied Linguistics 16, 15-34.
Clarke, M.A. (1979). Reading in Spanish and English: Evidence from adult ESL students. Language Learning 29, 121-150.
Cumming, A. (1989). Writing expertise and second-language proficiency. Language Learning 39, 81-141.
Cziko, G.A. (1980). Language competence and reading strategies: A comparison of first- and second-language oral reading errors. Language Learning 30, 101-116.
Eemeren, F.H. van & R. Grootendorst (1984). Speech acts in argumentative discussions. A theoretical model for the analysis of discussions directed towards solving conflicts of opinion. Dordrecht/Cinnaminson: Foris Publications, PDA 1.
Eemeren, F.H. van & R. Grootendorst (1992). Argumentation, communication, and fallacies. A pragma-dialectical perspective. Hillsdale, NJ: Lawrence Erlbaum Associates.
Eemeren, F.H. van, Grootendorst, R. & F. Snoeck Henkemans (1996). Fundamentals of argumentation theory. A handbook of backgrounds and contemporary developments. Mahwah, NJ: Lawrence Erlbaum Associates.
Flower, L. S. & J. R. Hayes (1981). Plans that guide the composing process. In: C. Frederiksen & J. Dominic (eds.), Writing: The nature, development, and teaching of written communication. Vol.2. Hillsdale, NJ: Lawrence Erlbaum Associates, 39-58.
Garssen, B. (1997). Argumentatieschema’s in pragma-dialectisch perspectief. Een theoretisch en empirisch onderzoek. Amsterdam: IFOTT 32.
Giacalone Ramat, A. (1992). Grammaticalization processes in the area of temporal and modal relations. Studies in Second Language Acquisition 14, 297-322.
Giacalone Ramat, A. (1993). Sur quelques manifestations de la grammaticalisation dans l’acquisition de l’italien comme deuxième langue. AILE 2, 173-200.
Giacalone Ramat, A. (1995). Function and form of modality in learner Italian. In: A. Giacalone Ramat (ed.), From pragmatics to syntax. Modality in second language acquisition. Tübingen: Gunter Narr Verlag, 269-293.
Kasper, G. (1992). Pragmatic transfer. Second Language Research 8, 203-231.
Kasper, G. & R. Schmidt (1996). Developmental issues in interlanguage pragmatics. Studies in Second Language Acquisition 18, 149-169.
Keenan, E. & B. Comrie (1977). Noun phrase accessibility and universal grammar. Linguistic Inquiry 8, 63-99.
Lo Cascio, V. (1991a). Grammatica dell’argomentare. Strategie e strutture. Firenze: La Nuova Italia.
Lo Cascio, V. (1991b). Proposals for an argumentative grammar. In: F.H. van Eemeren, R. Grootendorst, J.A. Blair & C.A. Willard (eds.), Proceedings of the second international conference on argumentation. Vol.IA. Amsterdam: SIC SAT, 530-545.
Lo Cascio, V. (1995). Categories and modal function in counterargumentation. In: Reconstruction and application. Proceedings of the third ISSA conference on argumentation. Vol.III. Amsterdam: SIC SAT, 78-95.
Lonzi, L. (1991). Frasi subordinate al gerundio. In: L. Renzi & G. Salvi (eds.), Grande grammatica italiana di consultazione. Vol.II. Bologna: Il Mulino, 571-592.
Odlin, T. (1989). Language transfer. Cambridge: Cambridge University Press.
Schoonen, R., J.H. Hulstijn, & B. Bossers (1998; forthcoming). Language-specific and metacognitive knowledge in native and foreign language reading comprehension: An empirical study among Dutch students in grades 6, 8 and 10. Language Learning 48/1.
Skiba, R. & N. Dittmar (1992). Pragmatic, semantic and syntactic constraints and grammaticalization: A longitudinal perspective. Studies in Second Language Acquisition 14, 323-349.
Toulmin, S. E. (1958/1964). The uses of argument, 2nd ed., Cambridge: Cambridge University Press.
Vedder, I. (1996). The acquisition of argumentation and the use of argumentative indicators in L2 by Dutch adult learners of Italian. In: The sociolinguistic dimension in the teaching and learning of modern languages. Proceedings of the 11th international conference, GALA 7. Thessaloniki: University Press, 407-412.
Vedder, I. (1998). Dunque l’Italia ha perso il suo fascino? Io penso di no. Argumenterend schrijven in een tweede taal. Een analyse van argumentatieve teksten van Nederlandse studenten Italiaans. University of Amsterdam: IFOTT/LOT 2.
Vignaux, G. (1991). A cognitive model of argumentation. Proceedings of the second international conference on argumentation. Vol.IA. Amsterdam: SIC SAT, 303-310

Introduction
The two schools are those of the fallacy critics and the argument analysts. The distinction I draw is in terms of areas of interest and emphasis within informal logic as exhibited in the writing of several informal logicians, and I will deal very much with general trends and tendencies. The distinction can prove useful, I maintain, even if a fallacy critic responds “I do some of the same things you ascribe to argument analysts.” The heart of the matter is where the writer places his or her highest priority, and how this affects the topics chosen and the methods of work.
Accordingly I will first distinguish the two schools by their different emphases and some typical writers, note what the two have in common, and touch on the development of informal logic as a discipline. There follows a treatment of two differing conceptions of argument. After this, some distinctions within each school are explored. Finally I summarize and conclude this survey and analysis.

2. The Schools Distinguished
Fallacy critics seize on informal logical fallacies as the main object of their study, such as begging the question or the ad hominem. They focus on argumentation in natural language where such fallacies occur, approaching it from the standpoint of a critic. They regard argumentation as a process, much as a drama critic observes the tragedy unfolding before her on the stage. Our drama critic (let us assume she is good at her job) will be sensitive both to the strong points of the production as well as to its weaknesses. But the fallacy critic is by orientation more sensitive to weaknesses or lapses in argumentation, since that is of course what logical fallacies are (whatever else they may be). On the practical side, the fallacy critic scrutinizes a text for fallacies and points them out, or finding none, allows that the text passes muster. On the theoretical side, the fallacy critic is interested primarily in a theory of criticism, which concerns what makes fallacious reasoning fallacious, and secondarily in a theory of argument, an explanation of the kinds of discourse and circumstances in which fallacies occur. The leading writers of this school are Douglas N. Walton, John Woods, Ralph H. Johnson, and J. Anthony Blair.
Argument analysts take argument in natural language as the main object of study. They tend to define argument broadly as any case of a claim or statement backed up with reasons. Argument analysts are inclined to regard argument as a finished product which they then slice up into its constitutent parts for study. Not being guided by traditional or recent notions of fallacies, analysts are more concerned with describing and categorizing discourse. They put more stress on distinguishing argument from related uses of language like problem solving and explanation. The analyst relates to argument much as a scientist to a specimen. The scientist analyzes the specimen then sums up the result of her analysis. Perhaps the main difference between scientist and analyst is that the scientist as such does not evaluate her specimen relative to human purposes, instead aspiring to remaining value free. The work of an argument analyst on a specimen, however, culminates in the judgment that the argument is weak or strong on the basis of how little or much support the premises provide for the conclusion.
On the practical side, the analyst identifies an argument, analyzes it, and then evaluates it. Not being focussed on fallacies, she may be more sensitive to the outcome being that the argument is strong or good. But typically no traditional or current literature provides her with a body of good-making features that would complement the bad-making ones of the fallacy critics. On the theoretical side, analysts investigate matters arising from their central activity like identifying and formulating missing premises of an argument, or distinguishing ways in which premises relate to an argument’s conclusion like convergent and linked. Leading writers of this school include Stephen F. Toulmin, Michael Scriven, Trudy Govier, David Hitchcock, Alec Fisher and James B. Freeman.

3. What the Two Schools Have in Common
The two schools share a strong interest in argument in natural language and the conviction that it is important to be able to deal with it effectively. They are agreed that traditional (e.g. syllogistic) and recent (e.g. symbolic) formal logics inadequately address this need, and that this inadequacy stems from the formalism of formal logics.
For a variety of reasons the need for techniques of analyzing and evaluating argument in natural language is deemed sufficiently pressing that a new (and hence informal) logic must be devised to address it. One frequently cited reason is that we must be able to analyze and evaluate natural-language discourse on matters of public policy in order to contribute and function effectively as citizens in a democracy.
Many informal logicians are linked by similar educational and disciplinary backgrounds, and by a strong interest in the teaching of logic. Most members of both schools are academically trained philosophers with more or less background in those formal logics brought to fruition in the 20th century, propositional and predicate calculi. Most have taught introductory level college courses in logic. Most came to reject the claim that such formal logics were the best vehicle for teaching the practical reasoning skills so sorely needed by many of today’s students. Most have a strong interest in creating teaching materials that reflect developments in informal logic for better addressing such needs. For example, all of the writers mentioned above (both schools) have authored or co-authored one or more college textbooks on informal logic, reasoning, or critical thinking designed for an introductory level course (Woods and Walton 1982; Johnson and Blair 1994; Toulmin 1984; Thomas 1986; Scriven 1976; Govier 1992; Hitchcock 1983; Fisher 1988; Freeman 1988).

4. Informal Logic as a Discipline
Although there is no dearth of theoretical work by argument analysts, the development of informal logic as a field – as a discipline – has been driven more by the fallacy critics. They may rightly be called fallacy theorists in this connection. Fallacy critics tend to think of themselves as logicians cultivating a sub-discipline of logic with an ancient history, a tradition (of questionable distinction), and comparative recent neglect. C.L. Hamblin (1970: 12) notoriously characterizes the typical modern textbook treatment of fallacies thus:
[It is] as debased, worn-out and dogmatic a treatment as could be imagined -incredibly tradition-bound, yet lacking in logic and in historical sense alike, and almost without connection to anything else in modern Logic at all. This is the part of his book in which the writer throws away logic and keeps his reader’s attention, if at all, only by retailing the traditional puns, anecdotes, and witless examples of his forbears.
Leading fallacy critics by and large subscribe to Hamblin’s assessment (but for a recent volte face on this see Johnson 1995: 153-166) and set themselves the goal of remedying (in different ways) weaknesses in this corner of logic.
Argument analysts are somewhat less inclined to view themselves as logicians, even though they accept being classed as informal logicians. Some seem sceptical that much of value is to be learned from the tradition of informal fallacies (Hitchcock 1995). The tendency is to either nod politely in the direction of informal fallacies or to simply ignore them. Accordingly argument analysts are much less inclined to view themselves as jostling with formal logicians for space and sunshine in the territory of logic. They are thus less engaged polemically with formal logic, and tend to be diffident toward viewing and explicitly defining themselves as logicians.
The development of informal logic as a discipline, aware of itself as a discipline, owes much to the writings of Woods & Walton of the 1970s and early 1980s (collected in Woods & Walton 1987), and to a number of articles and books by Walton since that time (e.g. Walton 1987; Walton 1992; Walton 1992a). But it owes as much and perhaps more to the prodigious activities and fierce energy of Johnson & Blair. A series of articles co-authored by them beginning in 1980 (Johnson 1995: 2-51; Johnson & Blair 1985) has stressed defining and developing informal logic as a discipline.
They organized three international symposia on informal logic, in 1978, 1983, and 1988, all at the University of Windsor in Ontario. They started up the Informal Logic Newsletter in 1978, which became the journal Informal Logic in 1985, and have ably edited this principal medium of communication for specialists in the field. All four fallacy critics are found frequently at meetings of learned societies, or (in Johnson’s case particularly) at conferences on critical thinking, informal logic, or argumentation, promoting the field by reading papers, conducting workshops, and serving on panel discussions. While there are many other able writers in the field of informal logic, these four may be more definitive of it as a field.

5. The Concept of Argument
Until recently much of the writing on the concept of argument came from fallacy theorists. As logicians they realized that formal logicians also work with a concept of argument. They wanted their endeavor to be distinct from that of formal logicians, so they sought to define argument in a distinct fashion. As is often the case, the impulse to push off in a new direction comes from dissatisfaction with current practice.
Argument analysts tend to agree with formal logicians that argument is adequately defined as cases of claims being backed up with reasons (cf. Hitchcock 1983: 31; Freeman 1988: 20). When we use arguments, we try to persuade in a rational way by citing evidence or reasons to back up our view. The evidence or reasons are called the premises, and the view being defended is called the conclusion (Govier 1985: 1) arguments are “discourses containing statements that are set forth as supporting, proving, or making probable what is said in other statements” (Thomas 1986: 10).
The main interest of analysts is in techniques of analysis and evaluation, and they tend to accept as argument those creatures their techniques applied to. Thomas (1986), for example, titles his textbook Practical Reasoning in Natural Language. He expects his readers to realize that natural language is distinct from the artificial languages of symbolic logicians (e.g. Russell-Whitehead notation, Polish notation), and also to realize that practical reasoning differs from theoretical reasoning (e.g. in mathematics or physics) by being of potential use in everyday life. For anyone who is unclear what “practical” means in this sense, Thomas includes recipes and claims from advertisements among his examples and exercises. This analyst definition of argument is a minimalist definition in its sparse defining features, but a veritable Jacksonian democracy in its broadly inclusive extension.
One might object that it is unfair to analysts to look to their textbooks for a fuller picture of the concept of argument, but at least in the 1970s and 1980s argument analysts devoted little attention to defining argument, even in their theoretical work. Thus e.g. Govier (1987: ch 2) devotes a chapter to the question whether a theory of argument is possible, but very little of it deals with what an argument is. I point this out not to claim that Govier should have dealt with this topic, but as evidence that for argument analysts “argument” was a relatively unproblematic concept.
What did render the concept problematic was initially fallacy critics, Johnson & Blair foremost, disputing the claim of formal logicians to have techniques adequate for the analysis and appraisal of arguments in natural language. These writers find argument defined by formal logicians in much the same way as it is by argument analysts among informal logicians. So in attacking the former target the latter comes into their crosshairs also.
On the positive side fallacy critics prefer to define argument by focussing on the socially interactive process which produces it. Many fallacies commonly classified as fallacies of relevance can be understood as violating rules of reasonable procedure in a dialogue. One can always criticize an ad hominem in the spirit of the above minimalist definition by indicating that the premises are irrelevant to the conclusion, making the argument weak. But exploring the dialogue in which it occurs, the roles of the participants, which moves are open to them and which closed, and which moves they ought to make, gives us a richer and fuller awareness of why an ad hominem is a fallacy. An issue of substance is being debated and serious reasons or evidence occupies the field, to all of which personal circumstances and characteristics of the participants are at most of peripheral significance. The participants have a duty to stick to the point, which one of them violates by dragging some personal trivia about the other into the debate. Thus the ad hominem fallacy, and Walton (1992b: 32) defines argument accordingly:
Argument is a dynamic social interaction, in which participants engage in a dialogue exchange … a social and verbal means that two parties can undertake together in order to resolve a conflict or difference between them.

Blair and Johnson (Johnson 1995: 92) prefer to stress the dialectical aspect of argument:
To say that argument is dialectical … is to identify it as a human practice, an exchange between two or more individuals in which the process of interaction shapes the product.

From the vantage point of this definition, Blair and Johnson (Johnson 1995: 90-94) criticize the minimalist definition on two counts:
1. It is structural rather than dialectical.
2. It views argument as product rather than process.
Argument as essentially dialectical is said to avoid such shortcomings.

These four features are stressed:
1. As product, an argument must be understood against the background of the process that produced it, i.e. background beliefs shared, or debated by the community.
2. The process of argumentation presupposes at least two roles – one a questioner of a proposition, the other the answerer of these questions.
3. The process of argumentation is initiated by a question or doubt of a proposition.
4. Argumentation is purposive – the questioner challenges the proposition, the answerer defends it.

Argument analysts too have conceived argument as dialectical, though they have come only more recently to employ this term, and though the idea has remained in the background of their work. The contrast Toulmin (1958: 6f.) draws between the mathematical logic he rejects and a logic concerned with the practical assessment of arguments on the jurisprudential model he which he advocates, closely parallels the Blair-Johnson contrast of a rejected formal deductive logic and argumentation as pragmatic (given of course the Anglo-American adversarial judicial process). More recently Freeman (1991: 17-26) explores dialectical aspects from the vantage point of an argument analyst.

6. Distinctions Within the Schools: Fallacy Critics
Among fallacy critics there are a marked differences on the role allotted formal logics in the criticism of fallacies. Many (if not most) informal logicians expect little illumination of informal fallacies from formal logics, especially from the varieties of first-order predicate logic that have become the 20th-century formal logician’s stock in trade. The group of influential and carefully argued papers by Woods and Walton in the 1970s and early 1980s (Woods & Walton 1989) are however the closest that leading informal logicians get to formal logic. Formal analysis here is both necessary and the best way of critiquing fallacies. But the logical systems drawn on are not linear descendents of the Russell-Whitehead first-order predicate calculus. For example, Kripke’s intuitionistic logic is called in service for the petitio principii, as is dialectical game theory for this fallacy and our above one of complex question, and a plausibility logic is drawn on for the appeal to authority.
Scriven, Van Eemeren, and Grootendorst expressed doubts (in discussion at the International Conference on Argumentation in Amsterdam, June 1986) whether the gain from such formal analyses is sufficient to justify wheeling this much heavy formal logical artillery into the field against informal fallacies. Groarke (1991) distinguishes successfully portraying the forms of informal fallacies from illuminating specific fallacies. He seems on target in granting the latter achievement yet denying the former. It isn’t at all clear to me that informal fallacies even have formal structures. Certainly they do not in the common sense that they are best described as instantiating invalid forms of argument, where “best” means “most useful for detecting and critiquing” the fallacy. And any fallacy best described as instantiating an invalid argument form would be a formal fallacy, not an informal one. Yet Woods and Walton frequently succeed in providing fresh perspectives and valuable insights into the informal fallacies they examine.
In subsequent writing Woods (1987) insists on “The Necessity of Formalism in Informal Logic,” and draws on a mathematical model to illuminate the question of a unified theory of fallacies (Woods 1994). Walton’s work on the other hand has developed more in the direction of the Amsterdam School (Eemeren 1987a; Eemeren & Grootendorst 1995) to view fallacies as violations of procedural rules of reasonable dialogue like “the failure to state or address an issue, failure to document a source of expertise, failure  to ask reasonable questions, failure to stick to the point, use of emotions to avoid argument [or] prejudicial use of unclear terms that may be vague or ambiguous” (Walton 1987: 328). He may have arrived at this point relatively independent of the work of van Eemeren and others, since he had already published a book on logical dialogue games (Walton 1984) before the work of the Amsterdam School was much known in North America.

Blair and Johnson (Johnson 1995: 87-90) are at the opposite pole from the early Woods and Walton on the use of formal logic for criticizing fallacies. Interestingly recent fuller bibliographies of work in informal logic (Hansen 1990 and Schmidt & Hansen to early 1998 in Hamblin 1970; 1998 reprint) list no articles by Johnson and Blair jointly or separately critiquing an individual fallacy.
In their estimate, formal deductive logic claims to provide the materials for adequate criticism of fallacies, but falls far short of delivering on that claim. These writers explicitly reject the claim that we are looking for true premises in an argument of valid form to constitute a sound argument. In fact, they would expunge the very terms “true,” “valid,” and “sound” from the informal logician’s vocabulary (Johnson however appears to re-introduce “true” in “The Problem of Truth for Theories of Argument, read at this conference). Blair and Johnson oppose argumentation in the dialectical sense to formal deductive logicians’ preoccupation with implication or inference. They also discourage the use of “implication” or “inference” in informal logic. Inference or implication is not necessarily dialectical in that it does not depend on exchanges between two persons. It is not necessarily controversial, and it can progress linearly; argument on the other hand is essentially controversial, so it can progress only against the background of diverse viewpoints.
The Blair-Johnson view of argument as necessarily dialectical may have developed in interaction with the Amsterdam School. Lately Walton (1989: 114f.) has taken the position that argument can be conceived as a semantic core “normally surrounded by pragmatic structures.” The semantic core comprises premises and conclusion, the pragmatic structures some at least of what Blair and Johnson term dialectical. Johnson (in a paper read at Conference 95 on Critical Thinking, George Mason University, June 1995) seems very close to Walton’s position with his distinction of semantic core and dialectical tier. If after traversing this distance you are wondering whether there is a sense in which fallacy critics are still fallacy critics, you might recall the traditional distinction of fallacies of equivocation from fallacies of relevance. Fallacies of equivocation tend to occur in the semantic core, those of relevance in the pragmatic structures/dialectical tier.

7. Distinctions within the Schools: Argument Analysts
There is a persistent trend among argument analysts to separate the tasks of identifying, analyzing, and evaluating arguments (even though in practice there seems always to be some overlap). To identify an argument is to pick it out from surrounding discourse that is not argument, and to do this by noting certain features distinctive to argument. The minimalist definition supplies the distinguishing features. They are as charged by some fallacy critics structural and they are based on argument as product. Yet they serve the purpose well enough to be widely used. To analyze an argument is to clarify how the premises are advanced in support of the conclusion, and occasionally to supply unstated premises. To evaluate an argument is to decide on the basis of the analysis, and relevant information external to the argument, whether the argument is weak or strong. The trend to distinguish these three tasks is strongest in the work of Thomas (1986) and those influenced by him, although it may be traceable back to Beardsley (1975) and is clearly present in others (e.g. Scriven 1976: 39 et passim).
Note that analysts define argument as reasons advanced in support of a claim, not as reasons supporting a claim. This is done not to avoid intentionality in the definition (where the intent to prove would count as proof itself), but to keep the identification of an argument separate from its evaluation. Reasons support claims only in successful or strong arguments; they are advanced in support of claims but do not actually support those claims in weak arguments. Weak arguments, however, remain arguments and are not by the circumstance of their weakness transformed into some non-argumentative form of discourse. That informal logic should deal with weak as well as strong arguments seems obvious, but that how one defines “argument” affects this objective is less so.

Another way of putting this is to say that analysts aspire to evaluatively neutral criteria for the purpose of identifying discourse as argument. For them “argument” is a descriptive term that classifies a piece of discourse as distinct from poetry or grocery list. There are still important differences among analysts, who by and large agree on this definition, over what is to count as argument. Thomas, for example (1986), takes explanations in general into the scope of argument. Scriven (1976: 65f.) does not count explanations by cause and effect as arguments, and other analysts (Govier 1987: 159-176; Hoaglund 1987) have countered with cases of explanation that are not argument and argument that are not explanation. It does appear that an explanation can clarify or reduce puzzlement without attempting to prove anything, i.e. without being an argument. But it also appears that some explanations, such as those used to justify actions as morally right or counsel against them as morally wrong, do claim probative force and hence might appropriately be treated as arguments.

Govier (1987: 65-74), following up a proposal by the moral philosopher Wellman (1971), refers to explanations that justify as conductive arguments. The jury is still out on whether “conductive” picks out a distinct species of argument, but informal logicians in general are restive with the traditional distinction of arguments into deductive and inductive. Analysts in particular have been pressed to look at what is netted by the criteria of the minimalist definition with fresh eyes, since some choose not to be guided by even improved accounts of informal fallacies. What fresh eyes have seen has been reported (in the absence of any accepted descriptive terms) by hand as arrow diagrams to depict claims of logical support. The arrow points from premise to conclusion and represents the claim that the premise provides at least some logical support for  the conclusion. Thomas (1986), Freeman (1988), and Fisher (1988) are among those analysts who make extensive use of diagraming, with Thomas and Fisher focusing especially on conditional or suppositional arguments. Analysts concentrating on types of argument where diagrams have yet to offer much aid use them correspondingly less. Govier (1992) with some emphasis on arguments by analogy loosely fits this description.

Diagramers fall into three groups, depending on the direction their arrows point: uppers, downers, and lateralers. The Amsterdam School of speech communication theorists are uppers (Eemeren & Grootendorst 1984: 93) as well as the analyst Finocchiaro (1980: 367, 378, 388f. et passim). But uppers have been the least influential of the three in North America. Toulmin (1984) and his followers are lateralers. They fit all arguments into one scheme beginning with grounds on the left, with warrants, backing, modality, and rebuttals all contributing en route to the claim on the right. In practice Toulmin’s lateral diagram functions somewhat like a flow chart of items to check off in analyzing and evaluating an argument. It does not distinguish argument types, and users of it encounter difficulty making the distinctions of grounds, warrant, and backup it calls for (Johnson 1995: 122-135; Freeman 1991: 49-88).
The downer technique which has now become “the standard approach” (Freeman 1991: 1) owes more to Stephen N. Thomas (1986) than any other single writer. Thomas states that he adapted this technique from the earlier work of Monroe Beardsley (1975), but the scope and facility of application contributed by Thomas have greatly extended its use among analysts. Thomas distinguishes four basic argument patterns: linked, convergent, divergent, and serial. The linked and convergent are arguments with a single conclusion whose premises work together in different ways. The other two patterns have multiple conclusions, the serial, one or more intermediate conclusions, and the divergent, two or more final conclusions.

Few topics have exercised analysts more than the distinction of linked from convergent arguments (e.g. Vorobej 1994; Conway 1991; Yanal 1984). Indeed fallacy critics (Walton 1996) and speech communication theorists (Snoeck-Henkemans 1992) have joined the debate. Roughly speaking, the premises of a linked argument must work together or cooperate to provide a measure of support for the conclusion. In the convergent argument each premise provides a measure of separate, independent support. Most arguments in formal logics, mapped onto informal patterns, are linked. Every valid syllogism, for example, has at least one universal premise and so at least one term distributed in its premises. Without this universal premise, the other premise usually contributes little support to the conclusion. Toulmin’s argument scheme also greatly favors linked arguments, since every argument will have grounds (facts of the case) and a warrant (general law) licensing the inference to the conclusion.
Analysts like fallacy critics have grappled with the problem of developing a terminology accurately descriptive of argument yet free of misleading associations carried over from formal logics. Toulmin (1958) uses “grounds” in place of “premise” to better distinguish his endeavor from that of formal logicians. Thomas prefers “reason” to “premise”, indicating that “the use of the term ‘premise’ is often taken to indicate that the reasoning in question is supposed to be deductively valid” (1986: 133). Deductive validity is a particularly inappropriate criterion of argument strength for informal logic, since judged by it nearly all natural-language arguments fail.
Another way of discussing argument strength in formal logic is to indicate that it is impossible for a formally valid argument with a false premise to prove its conclusion. This implies that every premise of an argument in formal logic is necessary, or that once correctly identified as a premise that statement is essential to the proof of the conclusion. The special problem for the analysts in informal logic arises in terming the support statements of a convergent argument “premises”. Since the convergent argument is one in which by definition each premise contributes a measure of separate, independent support, it is always possible that a given convergent argument may have one weak or even false premise yet still be strong (due to support contributed by other independent premises). However a premise cannot at the same time be a statement both essential and unneeded to establish a conclusion (Hoaglund 1988).
Facione (1989) would eliminate the strong argument with a false premise by blocking the use of “premise” in informal logic. But an important task of analysts is to uncover unstated or tacit premises (e.g vid. Grennan 1994; Govier 1989), and “unstated reasons” or “tacit grounds” does not seem to pick this out as effectively. Schmidt (1990) would interpret the convergent argument to comprise two or more separate arguments, a position also advocated by Gratton (1989: 3): “Since an arrow in the diagram of a convergent argument is supposed to represent an inferential link, or a link of support, … and since every link of support constitutes an argument, then the presence of two arrows implies that there are two arguments.” In the upper diagrams of the Amsterdam School (Snoeck-Henkemans 1992), the convergent argument contrasts with the linked as multiple compound to coordinately compound, and here too the convergent is interpreted as comprising separate arguments (Freeman in “Argument Structure and Disciplinary Perspective” read at this conference points out how this prevents multiple compound from coinciding with convergent arguments).
But this solution is very costly for informal logic. Without the convergent argument it is much harder if not impossible to do justice to most extended arguments. Pioneers of informal logic cite the need to deal effectively with extended arguments as a prime objective of informal logic (Johnson 1995: 19-22). Also, rejecting the convergent argument as a separate unit as suggested by Schmidt and Gratton imports into informal logic the same tunnel vision that has prevented formal logics from ever developing effective techniques for dealing with natural-language arguments. As Freeman argument depends on that specific argument: “Being essential to the cogency of an argument is an accidental property of some premises on some occasions. It is not part of the ‘essence’ of a premise” (cf. Hoaglund 1990).

8. Conclusion
To sum up, the starting point of fallacy critics is the logical tradition of informal fallacies. Early critics attempted to illuminate them by drawing on formal logics, but the recent trend is to situate the fallacies in their larger social context of debate and discussion. Analysts have worked with a minimalist definition of argument, and have struggled to understand different ways in which premises and conclusions can relate in the variety of arguments encountered in natural language. Critics differ over whether and to what extent formal logics are helpful for the problems of informal logic. Analysts differ over whether explanation counts as argument, and over what types of argument there are with the linked-convergent distinction
attracting much attention.
Limitations of time have prevented me from more than hinting at the fruitful interaction of informal logicians with the work of the Amsterdam School of speech communication. Nor have I even been able to hint at the connections (particularly of analysts) with those working in critical thinking in North America, where argument analysis is considered by some to be a model critical thinking activity. The briefest of references above to Peter Facione must suffice – Facione is the designer of the California Critical Thinking Test and is currently conducting research into critical thinking dispositions.
My purpose in drawing the distinction of fallacy critics from argument analysts is to aid those looking in on informal logic to better orient themselves toward work in the field, and to provoke informal logicians themselves to consider how what they are doing relates to work by others in the field.