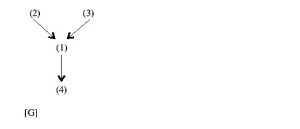ISSA Proceedings 1998 – A Few Remarks On The Individuation Of Arguments
1.
“An argument,” Irving Copi tells us in a much-quoted passage, “is any group of propositions of which one is claimed to follow from the others, which are regarded as providing support or grounds for the truth of that one.”[i] Copi’s usual elegance may have temporarily deserted him in the remark quoted, and his definition may be less explanatory than might be desired, but the general idea is clear enough – or at least clear enough for the great majority of people in this room to reject it. Where the Amstel flows and all pragmas are dialectical, propositional definitions of argument, such as Copi’s, have about as much purchasing power as the Indonesian rupiah. Not that that’s necessarily a mark – or even a guilder – against them, and not that that means that propositional views in general, or Copi’s in particular, aren’t worth exploring. Indeed, I think that examining what this Snidely Whiplash of argumentation theory – for so he’s many times considered – says almost always repays attention, and though my focus won’t be his definition of an argument so much as the related issue of the individuation of arguments, I think his views help to clarify both issues.
But let me introduce character number two in this little drama before getting back to Copi, character number one.
A more discourse-oriented definition of argument has been advanced by another arch-villain of argumentation theory, but one not nearly as often targeted for attack and refutation. According to Monroe Beardsley, “an argument is a discourse that not only makes assertions but also asserts that some of the assertions are reasons for others.”[ii] From the pragma-dialectical perspective, Beardsley’s definition may lack the shelter and clothing of the pragma and the dialectical, but at least it partakes of that staff of argumentative life, discourse. More striking than that single but pervasive difference between the two, however, that single but pervasive difference between Copi and Beardsley, are the similarities of their views. Substitute ‘set of propositions’ for ‘discourse,’ ‘propositions’ for ‘assertions,’ and ‘claims’ for ‘asserts,’ and Beardsley’s definition coincides almost precisely with Copi’s. If we bracket the discourse – or rhetorically- oriented elements of Beardsley’s definition, in other words, there is little difference between their views.
2
Which only goes to show that two people can basically agree on one fundamental issue – what an argument is – but profoundly disagree on other fundamental issues, such as what the identity of an argument consists in, and how to individuate arguments. To be clear about what I’m referring to here: the identity of an argument I take to be its self-sameness, the fact, in a sense, that it is what it is – namely, an argument, and, moreover, that argument — and not another thing, not even another argument. I know that’s not very enlightening, but it’s hard to say much more, on a general level, about what the philosophical issue of identity is than that it’s a metaphysical issue and concerns what constitutes, in the most important sense, the fact that a thing is what it is and not some other thing. Bishop Butler would no doubt be proud of me and give me his blessing for my remarks about identity, even if they’d win no awards for advancing the educated public’s understanding of philosophy. Anyway, when discussing the identity of a thing, philosophers generally speak of identity conditions for that thing, and many times the kind of a thing whose identity is being specified is built right into the statement of those conditions. In the case at hand, a typical statement of identity conditions would go something like this: x is the (numerically) same argument as y if and only if…..
Closely related is another metaphysical issue, that of individuation. When it come to arguments, the issue here isn’t so much what constitutes singleness as what constitutes diversity, or many-ness. Less cryptically, the central question of the individuation of arguments is: What makes discrete, numerically distinct arguments discrete, numerically distinct arguments? Obviously the two questions are related: to know what makes a given argument the argument it is would tell us what makes discrete, numerically distinct arguments exactly that – discrete, numerically distinct arguments. To a lesser extent, the converse holds as well: to know what makes numerically distinct arguments such would lend at least a bit of a hand in telling us what makes an argument the argument it is.
Lastly among these preliminary remarks, I should also mention that the questions of identity and individuation frequently have their closely related, but numerically distinct, epistemological cousins stand in for them. The ersatz relatives in question are: How do we know that arguments x and y are one and the same? and How can we tell that we’re dealing with one, two, three, or however many arguments? (And we also could, of course, ask epistemological questions about our general identity and individuation conditions: How do we know that they’re correct?)
3
Back to our principals, Copi and Beardsley. A minute ago I said that Copi and Beardsley basically agree about what an argument is, on what makes something an argument. (This is another way of saying that their definitions are similar.) Their views on individuation, however – I won’t be saying much more about identity from now on – are markedly different. The definition shared by Copi and Beardsley answers part of the question of the identity of argument – an argument, in contrast to a non-argument, has propositions that figure in it as premises, and so on – but it doesn’t go the full distance, it doesn’t tell us what the unique identity or singularity of particular arguments consists in. Nor does it answer the question of individuation: By what principle do we, or should we, count arguments? And, in fact, as already mentioned, Copi and Beardsley have very different views on that matter.
Before I go on to expose and criticize them, and also – surprise of surprises – defend and, in a sense, recover them, I have to make two other comments. The first is that Copi and Beardsley don’t discuss individuation under that heading or, indeed, under any heading whatsoever. Their brief remarks are embedded in the discursive prose of logic texts, texts which are intended to teach students basic concepts, techniques, and skills, and they have neither world enough nor time to linger over distinctly theoretical matters. Philosophical niceties, they perfectly well know, have to await occasions like this one, that is, the professional literature. I’ll return to the point later, at the end of this paper, as it will make some difference to my final assessment of their views.
Second, and perhaps surprisingly, neither have argumentation theorists paid much attention to the matter. Shame, shame! Since the field is all about arguments, since the metaphysics of arguments is a bound to affect other issues, both within and without argumentation theory, and since, after all, individuation is a central theoretical concern – well, I expected a bit more. As it is, my admittedly cursory inspection of the literature has left me with a handful of nothing – except a hazy memory that Douglas Walton briefly discussed individuation in one of his books.[iii]
4
What, then, are Copi’s and Beardsley’s views on individuation? Copi straightforwardly declares that “argumentative passages often contain more than a single argument,” which certainly seems correct. The simplest arguments, he says, contain a single premise which (purports to) support a conclusion:
(1)
↓
(2)
[A]
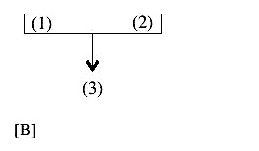
Sometimes, however, an argument contains more than one premise in support of a conclusion. When the premises work together – and let’s consider the simple case, an argument with only two premises – such an argument is diagrammed as
[B] is also a single argument, Copi thinks. Suppose, though, that two premises operate independently of each other. Suppose, in other words, that we have an argument like
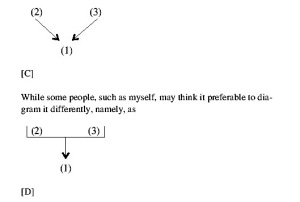
1.[The time for a national high-speed passenger railroad system has come.]
2. [Airlines cannot keep up, and in their frenzied attempt to do so have subjected passengers to poor service and, what is worse, life-threatening conditions.]
3. [The upkeep costs of the heavily travelled interstate highways, never intended or constructed to take such a pounding, are soaring.][iv]
According to Copi, this argument should be diagrammed as:
Let’s just assume that Copi’s diagram is fine as it stands, that the two premises do operate independently – after all, there surely are such arguments, and that’s all that really needs concerns us here – and return to the question of individuation. The question is, How many arguments does the passage, diagram [C], contain? Clearly recognizing that the question is one of individuation, Copi says that a decision must be made at this point about the ‘arithmetic’ of such arguments. Should we count this as a single argument with two premisses and one conclusion, or should we say that here we have two different arguments with the same conclusion? Emerging practice is to say that it is one argument with two independent premisses. The principle seems to be that the number of conclusions determines the number of arguments. So by a ‘single argument’ is meant an argument to a single conclusion, regardless of how many premisses are adduced in its support.[v] Count your conclusions, and you’ve counted your arguments. Thus Copi diagrams the following argumentative passage
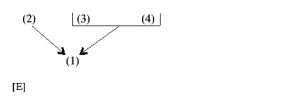
1. [Desert mountaintops make good sites for astronomy.]
2. [Being high, they sit above a portion of the atmosphere, enabling a star’s light to reach a telescope without having to swim through the entire depth of the atmosphere.]
3. [Being dry, the desert is also relatively cloud-free.]
4. [The merest veil of haze or cloud can render a sky useless for many astronomical measures.][vi]
Given his principle of individuation, he’s certainly right to refer to it simply as “an argument.”[vii]
Here as before, with the earlier quoted passage, a case could be certainly made for an alternative diagram, namely
In fact, what Copi himself says points in precisely that direction.[viii] As mentioned earlier, though, the point shouldn’t be pressed in this context. Considerations respecting argument analysis and diagramming are largely irrelevant when the issue at hand is individuation.
5
Beardsley does things rather differently. Without ever explicitly stating a principle of individuation, he considers the following passage Should it be legal for newspaper and television reporters to refuse to reveal their confidential sources? Indeed it should. For the reporter-informant relationship is, after all, similar to those of priest and penitent, lawyer and client, physician and patient – all of which have a degree of privacy under the law; moreover, if it were not protected, the souces of information needed by the public would dry up. It follows that Congress should pass appropriate legislation at once[ix] and refers to it as “a fairly simple argument”[x] – note the singular. The correct diagram of “the argument,”[xi] according to Beardsley, is[xii]
Diagrams, he adds, help us to understand the structure of an argument. This is especially true when an argument is as complex and “confused and confusing” as “the argument”[xiii] of the following passage:
1. [The present system of financing political campaigns is far too costly] because
2. [(under the present system it is) almost impossible for anyone who is not a millionaire or a friend (or employee) of millionaires to achieve high public office.] This is why
3. [the alternative system, under which elections are publicly financed, ought to be adopted;] but there is also the point that
4. [the public-financing system would help to democratize the process of choosing public officials by automatically involving every citizen in the process.]
5. [It would certainly be desirable to free legislators as far as possible from dependence on particular economic interests,] as well as
6. [(it would be desirable) to equalize the opportunities of candidates,] for
7. [their merits ought to count more than their money in elections.][xiv]
Its diagram is[xv]
As Beardsley rightly notes, diagramming such a passage helps us to “recast [an] argument… in a more orderly way.”[xvi] (Yet again, however, a maverick like myself might wonder whether Beardsley’s diagram really is correct. Do (1), (4), (5), and (6) really function independently of each other in supporting (3)?)
Further evidence that Beardsley disgrees with Copi can be found in his earlier and lesser-known but more comprehensive and detailed book – and probably better book – Practical Logic.[xvii] Practical Logic is a groundbreaking book in many ways: written in 1950, it’s exhaustive and clear, and among the first books of its kind.[xviii] Among other things, it introduced diagramming into the world of informal logic. In any case, and more to the issue of individuation: in Practical Logic Beardsley explicitly states that “In a long argument, some of the reasons will also be conclusions, for they will be supported by more fundamental reasons,”[xix] and “those conclusions that are not themselves used to support further conclusions we shall call the final conclusions of the argument”[xx] – note the singular “the argument.” Seemingly in agreement with Copi, he also says that “In a convergent argument” – note again the singular – “several independent reasons support the same conclusion.”[xxi] Thus, along with Copi, he holds that
A serial argument needn’t be so simple, though, Beardsley is quick to add, for not only could a further conclusion, (4), be drawn from (3), but a serial argument could also be convergent, divergent, or both in addition to being serial. All of this is certainly very much in keeping with what Beardsley says in Thinking Straight,[xxiii] but he’s more explicit here – so much so that he actually comes close to stating a principle of individuation when he writes, in summarizing the chapter from which the preceding quotations have been taken:
An argument consists of
1. one or more conclusions…;
2. one or more reasons… for each conclusion;
3. one or more logical connectives… indicating that the conclusions are inferred from the reasons.[xxiv]
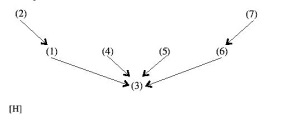
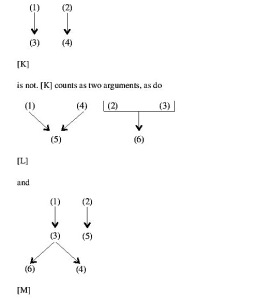
From these hints I infer – and I hope that this is an inference to the best explanation – that Beardsley’s principle of individuation is that arguments are individuated by interconnected inferential structures. Count arguments, in other words, by counting interconnected inferential structures, regardless of how many conclusions or inferences there are in such a structure. Thus every diagram above, including even so complex a configuration as [H], is a single argument, according to Beardsley, but (K)
is not (K) counts as two arguments, as do (L)
and
(M)
In brief, summary form, then: Copi individuates arguments by their conclusions, while Beardsley individuates them by their inteconnected inferential patterns, regardless of the complexity or extent of that pattern. For Copi, there is one argument per conclusion; for Beardsley, there is one argument per interconnected inferential pattern.
6
These are both interesting views, and I’ll have something to say in favor of each in a minute, but for now I want to say that, if individuation is taken strictly, neither is correct. Consider Copi’s view that (N) – see Figure N & text – Figure O
Problem number one with Copi’s view is that it has the highly counterintuitive implication that [N]/[O] is a single argument. Anslem’s proof and Aquinas’s Third Way are two different arguments if any arguments are two different arguments. That’s true irrespective of the fact that they share the same conclusion, and someone might think both cogent and thus offer both in support of theism. In point of fact, Aquinas himself propounds Five Ways, five proofs of God’s existence, and clearly thinks of them as five distinct arguments, even though they share the same conclusion, and even though all five are offered in the same context, The Summa Theologica, in the span of two short pages.
Reinforcing the point is a second objection, but one which focuses on argument assessment. Keeping the same example in mind, let’s suppose that there are very serious problems with Anselm’s proof but not with Aquinas’s reasoning. The Third Way is a godly success – as opposed to an ungodly one. Is the argument – remember, this is a single argument, according to Copi – very good, very bad, or somewhere in the middle? None of these answers will do. To say that it is very good ignores the grievous problems with Anselm’s proof; to say that it is very bad ignores the celestial success, the vast strengths, of Aquinas’s Third Time at Bat; to say that it is somewhere in-between ignores the fact that we’ve been given sufficient reason for the conclusion. A verdict of “in-between” isn’t a judgment made about a single argument but – as I would put it – a grade of “C” given to a passage in which two arguments appear, one excellent, the other not so good. All of this is reflected in our common belief that there can be two independent arguments for the same conclusion, two proofs or strong arguments that Walter L. Weber has rabies, that there are Russian arms in Afghanistan, that the integral of the function f(x) – x between zero and one is one-quarter, or that triangle ABC is congruent to triangle DEF.
7
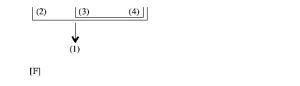
Since Beardsley would also count [N] as a single argument – it’s a single interconnected inferential structure – exactly the same two objections apply to him. Like Copi, he individuates arguments in a coarse-grained way, and counts what should be two or more as one. And I say “or more” because Copi and Beardsley would also count as a single argument, when simply interating my counterarguments above – let’s say that (3) incorporates considerations of design as an additional reason for God’s existence – it can be readily seen that the structure contains three arguments, strictly speaking. Beardsley’s problems run deeper than Copi’s, though, for he’s subject to all of the counterexamples that plague Copi, plus some that apply to him alone. Copi, for example, would say that 
contains two arguments. (For Copi, the number of arguments in a passage has to be at least n-1, where n is the number of vertical levels or lines in the argument diagram of the passage.) I think that Copi’s right about this, though not because [Q] contains two conclusions. Beardsley, however, would have to regard [Q] as a single argument. By doing so, he invites precisely the same sorts of objections that attend considering [N], [O], or [P] as a single argument. What, for instance, are we to say about this supposedly single argument if (7) does strongly support (8), but (8) lends virtually no support to (9)? As I’ve already indicated, the correct answer doesn’t seem to be any of the three alternatives, ‘very strong,’ ‘very weak,’ ‘somewhere in-between.’ The correct answer is that [Q] isn’t a single argument at all. [Q] contains two arguments, and one is very strong, the other very weak.
8
What, then, is the truth about argument individuation? My own view is probably evident from the above: individuate arguments by inferences. Count inferences, and you’ve counted arguments. In other words, every inference determines an argument, in the strict sense. Individuating arguments in this way would not only squelch the counterexamples that dog Copi and Beardsley, but also be more in keeping with what constitutes an argument. The essence of an argument, after all, is neither premises nor conclusion, for considered independently of an inference, both are mere propositions (or sentences, or statements, or beliefs, depending on your theory of argument). It’s an inference that makes a proposition a premise, that makes a proposition a conclusion, and thus that makes a batch of propositions an argument – and an argument as defined by both Copi and Beardsley: premises related to conclusion in a certain way. I’m thus lead to individuate arguments by inferences on the basis of three considerations (one not yet mentioned):
(a) the elimination of the counterexamples that plague Copi and Beardsley,
(b) reflection of the nature of argument, and, in truth,
(c) a dearth of plausible alternatives.
Strictly speaking, arguments should be individuated in a fine-grained way, by inferences.
9
But I’ve repeatedly used the phrase “strictly speaking” in the above, and since The Netherlands is hardly a land known for its strictness – even now we’re not five minutes walking distance from the ladies in the window – some people may wonder what I have in mind with this qualifying phrase. Well, what I have in mind is that if Copi and Beardsley were doing philosophy and writing journal articles, they would deserve even more scorn than I, with my big hands, and my brethren here in the audience, with their even bigger hands, could heap upon them. They should have been more attentive, more careful, more thorough than they were – and, honesty requires me to say, at least as far as thoroughness is concerned, than I’ve been here.[xxv]
But, of course – and this is where the “strictly speaking” comes in – they weren’t even attempting to do rigorous philosophy or write a journal article. They were each in the middle of the very first chapter of their excellent logic texts, and were trying to help students, at the very beginning of their study of good reasoning, to get a feel for the nature of argument without bogging them down from the start with confusing and unnecessary subtleties. Their job – and this is decidedly practical, even if not pragma – was to inculcate concepts, principles, rules, techniques, strategies, abilities, and attitudes, which is a daunting enough task without simultanelously trying to please a very different crowd, that of punctilious philosophers filled with grief, grievances, and grudges that passeth understanding, and ready to pounce on their fellow philosophers with the only true joy that they find in life. Pardon may not be the word for all, though there is much to recommend in Shakespeare’s remark to the contrary, but certainly something more than mercy is called for in the case of Copi and Beardsley. Justice, rather, demands that the charges be dismissed.
If that isn’t clear on pragmatic grounds, on the grounds that their views on individuation are misconstrued if taken as pieces of theoretical philosophy, a further defense is available in the fact that there’s an extended but very common sense of the term ‘argument’ in which we aren’t so demanding, so nit-picking, so “strict sense”-oriented, a sense in which don’t and aren’t even tempted to individuate arguments by inferences. There is a sense of the term, for instance, and one frequently employed in everyday life, in which we do individuate arguments by conclusions – I’m speaking of Copi here, of course, but I’ll get to Beardsley in a minute. In this sense – and it’s one of several related senses – we say things like “the argument of the passage is that…,” where we fill in the dots with a number of different independent reasons offered in support of a single conclusion: The argument of the passage is that John won’t be able to make his mortgage payments this month, since his financial over-extension has caught up with him, and he’s just suffered several major business set-backs as well. We may recognize all the while that the passage actually contains several independent arguments, in the strict sense of the term, that all share the same conclusion; we may recognize, in other words, that the situation is really like [C], [E], [N], [O], or [P] above. Still, that doesn’t stop us, for we know that it’s perfectly fine and pragmatically preferable to consider such structures single arguments. No harm is done by individuating arguments this way, by conclusion, and efficient communication and naturalness are gained. It may be loose talk to speak so, to consider [E] or [N] as a single argument, but much of our talk about arguments is loose talk, but innocuous enough for all that.
But if Copi can be vindicated, at least to some extent, by such considerations, so can the even more nefarious Beardsley. The same general points come to the rescue: we speak even more loosely, but not incorrectly, in saying such things as: The argument of the passage (or chapter, or book, or whatever) is that the population of third-world countries is increasing, and so is their demand for consumer goods; we can therefore expect ever-increasing pressures on the environment, and so should immediately take steps to ensure that pollution levels remain within reasonable limits. We may realize that a summarized passage or an argument diagram actually contains numerous, numerous arguments, in the strict sense of the term – the situation may be like [H], or even more complicated – but we also realize that no harm is done by, and there are advantages to, taking the passage or diagram to contain a single argument, at least as long as there is one interconnected inferential structure that points to – to use Beardsley’s terminology – “a final conclusion or final conclusions.” If my point here isn’t clear in the abstract, think, to cite just one example, of how pedantic and cumbersome it would be to consider a long proof in predicate logic as a series of arguments, say, twenty or thirty, all told. Much better would be to think of it as simply a proof, or a deductively valid argument, with a final conclusion.
And speaking of final conclusions: May you buy the argument – note for the last time the singular – of this paper.
NOTES
[i] Irving Copi and Carl Cohen, Introduction to Logic, 8th edition, Macmillan Publishing Company, New York, New York (1990),p. 6.
[ii] Monroe Beardsley, Thinking Straight, 4th Edition, Prentice-Hall Publishing Company, Engelwood Cliffs, NJ (1975), p. 12.
[iii] When pressed, though, I couldn’t locate the passage in question or even remember which book of Walton’s it was in. This problem has since been partly remedied, however. At my request, Walton kindly told me that Argument Structure: A Pragmatic Theory, University of Toronto Press, Toronto (1996), contains his latest and most complete discussion of individuation. Unfortunately, I didn’t find this out until after this paper was completed. In addition, when this paper was presented at the University of Amsterdam, James Freeman pointed out to me that he has a chapter on argument individuation in “a book sufficiently obscure to ensure that no one knows that it exists.” Although I still haven’t read Freeman’s paper, I’ll certainly take it, Walton’s work, and other discussions I might have missed into account in future work on individuation.
[iv] Copi, op. cit., p. 19. Copi is quoting Leo D. Marks, “Time to Start on High-Speed National Rail,” The New York Times, October 15, 1988.
[v] Copi, op. cit., pp. 19-20.
[vi] Copi, op. cit., p. 21. Copi is quoting Blanchard Hiatt, University of Michigan Research News, vol. 30, nos. 8-9, August-September 1979, p. 5.
[vii] Copi, op. cit., p. 20.
[viii] Copi says that “the two statements (3) and (4) must work together to support the claim that desert locations are good sites for telescopes.” By the same token, it could be said that the three statements, (2), (3), and (4), must ultimately work together to support the claim that desert mountaintops which is what the conclusion, statement (1), is about – are good sites for telescopes. Copi, op. cit., p. 21.
[ix] Beardsley, op. cit., p. 16.
[x] Beardsley, op, cit., p. 16.
[xi] Beardsley, op, cit., p. 16
[xii] Beardsley, op. cit., p. 17.
[xiii] Beardsley, op. cit., p. 18
[xiv] Beardsley, op. cit., p. 18.
[xv] Beardsley, op. cit., p. 18
[xvi] Beardsley, op. cit., p. 19.
[xvii] Monroe Beardsley, Practical Logic, Prentice-Hall, Inc., Englewood Cliffs, NJ (1950).
[xviii] I also think of Max Black, Critical Thinking, Prentice-Hall, Inc., Englewood Cliffs, NJ (1946), and Susan Stebbing, Thinking to Some Purpose, Pelican Books, Harmondsworth, Middlesex, England (1938), in this context. Neither of these books, however, is as comprehensive, clear, thorough, or practically-oriented as Beardsley’s. Nor are any other pre-1950 books.
[xix] Beardsley, Practical Logic, op. cit., p. 12.
[xx] Beardsley, Practical Logic, op. cit., pp. 12-13.
[xxi] Beardsley, Practical Logic, op. cit., p. 19.
[xxii] Beardsley, Practical Logic, op. cit., p. 19.
[xxiii] A close look at Beardsley’s definition of an argument, which is quoted above in section I, shows that he allows an argument to have two or more conclusions. An equally close look at Copi’s definition, which is also quoted in section I, shows that he doesn’t allow that.
[xxiv] Beardsley, Practical Logic, op. cit., p. 26.
[xxv] This paper just scratches the surface as far as argument identity and individuation are concerned. I address the matter at greater length in a companion piece, “Argument Identity,” in preparation.