ISSA Proceedings 1998 – Dividing By Zero – And Other Mathematical Fallacies

• by: Lawrence H. Powers - Wayne State University

In this paper I shall discuss a fallacy involving dividing by zero.  And then I shall more briefly discuss fallacies involving misdrawn diagrams and a fallacy involving mathematical induction, I discuss these particular fallacies because each of them seems at first – and seemed to me myself at one time – to be a counterexample to a theory of mine. The One Fallacy Theory says that every real fallacy is a fallacy of equivocation, of playing on some sort of ambiguity. But these particular fallacies do not seem to involve ambiguity, and yet they do seem to be real fallacies.[i] Let me begin with the dividing-by-zero fallacy.

It goes as follows:
1. Let a = b
2. So a2 = ab (multiply each side by a)
3. So a2 – b2 = ab – b2 (subtract b2 from each side)
4. So (a + b)(a – b) = b(a – b) (factoring)
5. So a + b = b (cancelling (a – b) on each side)
6. So 2b = b (since a = b)
7. So 2 = 1 (cancelling b on each side).

Now this argument appears to be a counterexample to my theory. Each step is stated in unambiguous algebraic terminology. The invalid move takes us from an unambiguously true equation 4 to an unambiguously false equation 5 by a move of cancelling a -b which is unambiguously though not obviously a division by zero. There seems to be no ambiguity.

My theory then seems to imply that there is no real fallacy; we do not have an invalid step which appears, by virtue of a covering ambiguity, to be valid, but rather a naked mistake with no appearance of goodness. A naked mistake is not a true fallacy.
But surely, the argument is a real fallacy. For it passes the phenomenological test. The first time I myself saw this argument in a book, I went through it carefully looking for the wrong step. And I could not find it, at least not just by going through the argument step by step. It looked like a proof to me, and at a time when I knew there had to be something wrong and was, in an intellectually serious way, looking for the mistake!
So clearly the argument is a real fallacy. It therefore seems a counterexample to my theory.
Now in trying to defend my theory, I think as follows. If a serious person is taken in by an invalid argument A/ .. B and ‘A’ and ‘B’ are not ambiguous, perhaps there is some other reasoning in the person’s mind. Perhaps he thinks that A implies C and C implies B, and it is the interpolated term C which is ambiguous. Another person who accepts A/ .. B may accept it for a different reason, using a different confusion, say A/ .. D/ .. B.

I therefore ask: Why did I myself think the argument dividing by zero was valid step by step?

It is often said that people divide by zero, as in our example, because you can usually divide and people just forget about the special case of zero. I have never liked this kind of explanation. How can one just forget about special cases? If the rule is that you can always divide unless the would-be divisor is zero, how can one apply this rule without determining whether the would-be divisor is zero?
At any event, the explanation about forgetting the special case did not apply to me. I didn’t forget the special case. I had never heard of any such special case. I learned from studying this very fallacy that one can’t divide by zero. I was astounded to find that one couldn’t always divide! I thought that you could always divide and that I knew you could always divide.

Now here too there is a popular explanation about why people think they can always divide. The explanation is that people overgeneralize: since you can almost always divide, we overgeneralize and thin we can divide in the case of zero also. I do not like this explanation. Such inductive reasoning could easily lead a rational person to think that one can always divide, probably. However, mathematical knowledge is not about what is probably true but about what is proven. I thought I knew that one can always divide, that I had seen a proof of this.
Now after examining the argument and not finding the mistaken step, I substituted the concrete number 5 for a and b. The equations then became: Let 5 = 5. So 25 = 25. So 25 – 25 = 25 – 25. Upon factoring, 10 { 0 = 5 { 0. Cancelling, 10 = 5. So 10 = 5. So 2 = 1. And here it is obvious where the mistake is. The equation 10 { 0 = 5 { 0 balances, but 10 = 5 doesn’t.
And reflecting on this wrong move, we see that its general form is x { 0 = y { 0/ .. x = y. So if we can divide by zero, then all numbers are equal. This proves that we cannot divide by zero. Of course, when I saw this, I distrusted my reasoning and went and looked in a math book to assure myself that it was really true that you can’t divide by zero.

Having thus decided that you can’t divide by zero, I started to consider my reasons for thinking you can divide by zero. How can it be that we can’t divide by zero? After all, I first thought, multiplication is always well-defined. But division is defined as the inverse of multiplication. Doesn’t it follow that division is always well-defined as well? I knew immediately that there was something wrong with this reasoning. In the natural numbers, it is always possible to add but one cannot always subtract, say, 7 from 3. Yet subtraction is defined as the inverse of addition. How then can it be that one can’t always subtract?

To understand this fallacy more clearly, let me state my argument in more sophisticated terminology. In modern logic, definite descriptions are well-formed expressions whether they refer or not. Thus, in a Russellian sense, ‘the king of France’ is a well-defined expression. And so, for any x, is ‘(¡ z)(x = z { 0)’. But the latter is the definition of ‘x/o’, which is thus well-defined, in a Russellian sense. For Frege, however, a referring expression is not well-defined unless it is proven that it actually succeeds in referring to something. Mathematicians speak of functions as being ‘well-defined’ in Frege’s, not Russell’s sense. If x/o were well-defined in Frege’s sense, then division by zero would be possible. So my argument involved an equivocation, on two different meanings of ‘well-defined’.

When, years ago, I fell into the dividing-by-zero fallacy, I found that one can’t divide by zero, and asked myself ‘how can that be?” I then went through the ‘well-defined’ problem as just rehearsed. However, when I saw that there were two different concepts of ‘well-defined’ involved, I did not feel that this point really addressed my perplexity, for I thought I had somewhere seen a proof that division always was well-defined, even in Frege’s sense. Hadn’t I seen a proof that you can always divide? Before looking at the proof I had in mind at that time, it is convenient here to consider another possible supposed proof.
In a book, Lapses in Mathematical Reasoning, the authors, Russian mathematicians, mention fallacies in which a true mathematical law is applied but in the wrong field of numbers. (Brades et. al. 1963: 14) It is interesting that fallacies involving dividing by zero can be thought of as a subclass of those applying a true law in the wrong field of numbers, and these in turn are a subclass of fallacies of ambiguity.
When we learn about numbers in our school years, we learn to use the word ‘number’ ambiguously. At first the teacher says that numbers are those things you count with: 1, 2, 3, 4, etc. So we learn to use ‘number’ to mean a natural or whole number, a positive integer. In this sense of ‘number,’ we learn that we can always add and always multiply, but we cannot always subtract or always divide. For instance, we cannot subtract 7 from 3 or divide 3 into 7. But then later the teacher told us that, after all, we could always divide as well as always add or multiply, though we still could not always subtract. We could now always divide because, the teacher said, “there are more numbers than you yet know about.”
Even as a youngster, I was rather hyper about ambiguity, and I said – though to myself, not out loud – “Come on, teacher, there aren’t more numbers than we know about. The truth is: you’re going to change the meaning of the word ‘number’”. And so it happened. Now ‘number’ meant positive rational, the fractions were numbers, and we could always add, multiply, and divide. With ‘number’ in this meaning, any number whatsoever could be divided by any number whatsoever, without any exception whatsoever.
Later the term ‘number’ will be extended again, from the positive rationals to the rationals generally. Now subtraction will always be possible, as well as addition and multiplication, but division by zero will not be possible.
And so one fallacious way of dividing by zero would be to apply the true law that division is always possible – true in the positive rationals, but to apply this law wrongly to rationals generally. This way of dividing by zero would involve equivocation on the term ‘number’ and so would be in accord with the One Fallacy Theory.

Still, when I myself divided by zero, I did not do it in this way, I believe. I knew that ‘number’ was ambiguous. I knew that when you extend the number system, as from positive rationals to rationals generally, in order to make a new operation, as subtraction, always possible, you have to recheck the previously always possible operations – addition, multiplication, and division – to make sure they are still always possible. But I thought I had seen in my readings just such a rechecking, a proof that these operations were always possible in the rationals generally.
So I recalled the argument in question. Take addition. Addition was always possible in the positive rationals and subtraction is now always possible. So let a and b be positive. Then a + b always exists. But a + (-b) is a – b and also always exists. And (-a) + (+b) is b – a and always exists. And, finally, (-a) + (-b) = -(a + b), a negative, and always exists. So addition is always possible, it seems. But the exact same argument can be given for multiplication and division. So they are all always possible.
Of course, the mistake in this argument becomes clear when we look at the version concerning division. But it is already there in the argument for addition. By considering a and b and -a and -b, I consider the positive numbers and the negative numbers but I forget to consider zero. What about zero!?
But this seems rather embarrassing. I said at the outset that I didn’t like the explanation that people divide by zero because they simply forget the special case of zero. Yet here I seem to have done precisely that! I just forgot about zero. How could I just forget about zero??

If there are three kinds of numbers, the positive, the negative, and zero, then in order to prove something about all numbers, you have to prove it about all three kinds, and not just about two. If there are three people, Arthur, Barbara, and Carl, in a room and I argue that all the people in the room are tall because Arthur is tall and Barbara is tall and I just forget about Carl, who is short, then that argument is not a fallacy; it is just a stupidity. Surely I couldn’t have just forgotten about zero!
Actually, I don’t think I just forgot about zero in the above reasoning, rather I vaguely thought I had covered zero twice over, though in fact my reasoning was not valid for zero. For I tend to use the terms ‘positive’ and ‘negative’ both strictly, excluding zero, and loosely, including it. So by proving something for all positives and negatives, I vaguely felt I had proven it for zero.
First, zero seems positive in some ways. It is a square number, equal to 02. It is its own absolute value. It is the end point of the positive half of the real line. By the familiar end point ambiguity, an end point seems both to be and not to be a point of the line segment whose end point it is. Also the positive and negative segments are two halves of the real line, and two halves seem to complete the whole. And if zero seems to be positive, then -0, which is also 0, seems also to be negative.
Given that 0 seems in some ways to be positive and negative, the basic reason I tend to use these two terms ambiguously is because it is convenient. We wish to prove results about an infinite class of things, the numbers. We cannot prove results about the numbers one by one, so we divide them into large classes, such as the positives and the negatives. If it happens that there are special cases, such as zero, which do not exactly fit into these large classes, we tend to include or exclude the special cases into the large classes. For the purpose of one proof, we think of zero as positive, for another, as negative, for another as both or neither.
We have a tendency to stretch and contract the more general class terms to include and exclude the special cases, as convenience dictates. This, I think, is why the argument that we could always divide in the rationals generally sounded correct to me. As I said, when I proved the result for all positives and all negatives, I vaguely thought I had covered zero twice over. This general sort of fallacy, shuffling the special case in and out of the general classes, I shall call the ‘special case fallacy.’ It turns out that a variant of this fallacy is used in the remaining two fallacies I wish to discuss.
Misdrawn diagram fallacies in geometry seem at first to be counterexamples to my theory. The problem is in the misdrawn diagram, not in any ambiguity in the language used in discussing the diagram. Yet I clearly remember being shown an argument involving a misdrawn diagram and being unable to see the error in it. However I shall I argue that the diagram itself is a representation and therefore can be ambiguous. In other words, the diagrams are not really misdrawn so much as misinterpreted.

In looking over various examples of this sort of fallacy in the Lapses book, I did not find one simple enough to present here in detail. However the ones I looked at generally had a common form. In the givens we are told that there is a point with property P. Call this point A. We are told also that there is a point with property Q. Call this point B. We represent this by drawing two representing points, labelled ‘A’ and ‘B’. In the reasoning which follows, we are asked to consider the line from point A to point B. We show that this line has property X. Then we show it has property not-X. We seem to have proven a contradiction.
The solution is that point A and point B are the same point. So there is not line from A to B. (Brades 1963: 22) The fallacy can be thought of as an example of the special case fallacy. When we originally draw the representing points ‘A’ and ‘B’, these are floating points which may or may not coalesce. They represent that there is an A and a B, which may or may not be identical.
Given A, then B may be the same as A, the special case, or anywhere else, the more general subcase. So the representation assimilates the special case to the general case; the two points, so to speak, may be one. But then, when we agree to draw a line from A to B, we misinterpret the representation as representing that A and B are different, two strictly, the more general subcase excluding the special case.
Therefore it is a fallacy of ambiguity, after all: the ambiguity of the representing diagram.

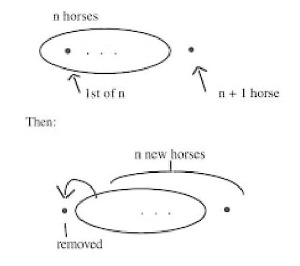
A very similar analysis can be given for the last fallacy I want to look at. Here we set out to prove that all horses are the same color.373 We ‘prove’ this by ‘proving’ by mathematical induction that, for any n, any n-membered set of horses has the same-color property, namely the property that all its members are the same color. The ‘theorem’ is obvious for n = 1, for any set of only one horse has all its members the same color. So we need to prove the inductive step: if every n membered set has the same-color property, so does any n + 1 membered set. We illustrate the argument for n = 5, n + 1 = 6, but this case is to stand in for general n and n + 1. We have a set of five horses and a sixth horse. All the 5 horses are the same color. Remove the first of the 5 and consider all the remaining horses. These again are 5 horses and all have the same color. Therefore all 6 horses are the same color. QED. So all horses are the same color.

Now the mistake in this ‘proof’ is that the argument for the inductive step works for any n and n + 1 with n more than 1, but does not work when n is 1 and n + 1 is 2. We do not notice this because, I think, we abstract from the 5 and 6 case a mental picture which plays the role of a misleading diagram.

This picture looks like this:

Here the first big dot is the first horse. The second is the n + 1 horse. The three dots represent whatever is left of the n horses, the first excluded. The ambiguity in this representation is in the meaning of the three dots. It originally represents all but the first of the initial n members, if there are any but the first. It is then misinterpreted as meaning that there are such remaining members. Initially the special case of there being no remaining members is included, but then it is excluded. So here again we have a special case fallacy, and we also have a misdrawn – or really misinterpreted – diagram fallacy, although now the diagram is not actually drawn, but is a mental picture.
In this paper, I have considered three mathematical fallacies which at one time I thought were counterexamples to my One Fallacy Theory. In each case, I have argued that these fallacies can be analyzed as fallacies of ambiguity after all.

NOTES
[i] My thanks to R. De Souza, who chided me about holding a theory to which I seemed to know counterexamples. His comments led me to explore these examples more thoroughly.

REFERENCES
Brades, Vm., Minkowski, Vl., Kharchiva, Ak., translated by J. J. Schorr-Kon (1963, originally published 1938). New York: MacMillan.

You May Also Like

ISSA Proceedings 2006 ~ The Criminal Abduction Paradox

ISSA Proceedings 2006 ~ A Discussion Of Habermas’ Reading And Use Of Toulmin’s Model Of Argumentation

ISSA Proceedings 2006 ~ The Rules Of The Critical Discussion And The Development Of Critical Thinking

ISSA Proceedings 2006 ~ An Analysis Of Preschool Hebrew Speaking Children’s Arguments From The Perspective Of The Pragma-Dialectical Model

ISSA Proceedings 2006 ~ Putin’s Terrorism Discourse As Part of Democracy And Governance Debate In Russia

ISSA Proceedings 2006 ~ Cultural Differences In The Persuasiveness Of Normatively Strong And Normatively Weak Expert Evidence

Comments