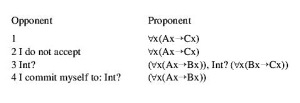ISSA Proceedings 1998 – The Use Of Ambiguous Expressions In Discussions

The fallacy of misusing lexical ambiguity in argumentation is called the fallacy of equivocation. I will explain what the fallacy consists of by sketching a dialectical situation. Starting from the notion of a precization, I will explore some possible moves of the opponent and proponent in that situation.
My main conclusions will be that it is polysemy rather than ambiguity in a narrow sense that is at the bottom of the fallacy of equivocation and that, partly in consequence of this, the proponent has some interesting possibilities after the opponent has detected the ambiguity. Before one accuses someone of the fallacy of equivocation one should not only check if a distinction is apt, but also whether there is any reasonable defence for the proponent.

1. The fallacy of equivocation
Equivocation is the fallacy of the misuse of the multiple meanings of an expression in argumentation. Two examples are:
(1) The money is in the bank, the bank is by the river, so you should go to the river. (Walton 1996: 72)
(2) All acts prescribed by law are obligatory. Nonperformance of an obligatory act is to be disapproved. Therefore, nonperformance of an act prescribed by law is to be disapproved. (Hamblin 1970: 292)

What’s wrong with these arguments? I will focus on the second, more realistic example. We can best understand the function of the elements of the argument from the perspective of a persuasion dialogue or critical discussion (Walton & Krabbe 1995: 68, Van Eemeren & Grootendorst 1992: 34). A proponent tries to persuade an opponent of his thesis. To achieve this end he needs a strategy.
The proponent should offer reasons that are plausible to the opponent. If the opponent does not object to these reasons, they count as commitments that cannot be withdrawn without explanation. The proponent will then have to show that the opponent is inconsistent when she is committed to the reasons that form part of his argument, but still maintains her critical attitude towards the thesis.
That means that when we are confronted with an argument for a thesis, we can evaluate the argument by (1) examining the plausibility of the reasons relative to the opponent and (2) checking if the position in which one is committed to the reasons but criticizes the thesis is inconsistent. So the evaluation is partly dependent upon the choice of the opponent. This choice is dependent upon the end of the evaluation. One can be interested in the tenability of the argumentation relative to oneself or relative to another actual or imagined group or individual.

When we imagine some reasonable and charitable opponent and look at the second example, we see an argument that could be successful. Both reasons have a certain plausibility. Acts prescribed by law are obligatory in a sense, because nonperformance of an act prescribed by law is often followed by sanctions of some sort. And nonperformance of an obligatory act is to be disapproved in a sense, because we should disapprove of the nonperformance of an act that one should perform. So, there is some ground to expect that this reasonable and charitable opponent will commit herself to the reasons.
We can picture the relevant fragment of dialogue as follows. Moves one and two form the confrontation stage, moves three and four are part of the argumentation stage (van Eemeren & Grootendorst 1992: 35).

(3)
Ax: x is an act prescribed by law
Bx: x is obligatory
Cx: nonperformance of x is to be disapproved

After the opponent has conceded the reasons, the proponent is in a strong position. He can ask her again to accept the thesis. And if the opponent refuses, he can accuse her of being unreasonable. For the thesis follows logically from the reasons, the denial of the thesis is inconsistent with the truth of the reasons. To back this up, he can prove this within predicate logic.
In models for discussion that do not provide the critical instruments for the opponent to handle this kind of situations, for example RPD (Walton, Krabbe 1995: 154-163) or Systems 1, 2, 3 (Mackenzie 1989), the proponent can win an easy triumph.

But that does not mean that the opponent would lose in a more complete model for discussion. For the expression ‘is obligatory’ represented by ‘Bx’, and thereby both reasons, represented by ‘.x(∀x->Bx)’ and ‘.x(Bx->Cx)’, can be subjected to a distinction (Crawshay-Williams 1953, Rescher 1977, Mackenzie 1989). The participants in the discussion should be more precise (Naess 1953, Crawshay-Williams 1957, Pinkal 1995).

‘Obligatory’ can be interpreted in a legal sense or in a moral sense. How should we read the reasons and consequently the commitments? A better representation of the dialogue is the following. A questionmark before a reason or commitment means that it is open in what way the statement should be interpreted.

(4)

In a legal sense of obligatory it is definitely true that acts prescribed by law are obligatory. And in a moral sense of obligatory it is definitely true that the nonperformance of an obligatory act is to be disapproved. So if the opponent was aware of the double meaning of ‘obligatory’, she would probably have committed herself only to those statements.

Walton (Walton 1996: 66) describes the fallacy of equivocation as a mixing up of different arguments. The proponent seems to give one good argument, but actually he gives several defective arguments. These defective arguments can be reconstructed by substituting for ‘obligatory’ either ‘legally obligatory’ or ‘morally obligatory’. Either both reasons are acceptable for the opponent, but then each argument contains ‘obligatory’ in a different sense, and the thesis does not follow. Or both reasons contain ‘obligatory’ in the same sense, so the thesis follows, but then one of the reasons is not acceptable for the opponent.

2. The defence of the opponent
When the opponent detects the ambiguity in the reasons adduced by the proponent before she commits herself to the statements, she should request the proponent to make his reasons more precise. But it is also possible that the opponent finds herself in the situation that she has already committed herself to statements that turned out to be ambiguous. In this situation too she should be able to make her commitments more precise. I will start from this latter and more difficult situation.

Her defence could be expressed like Mackenzie’s Distinguo! (Mackenzie 1988). ‘I distinguish between two different senses of ‘obligatory’, “morally obligatory” and “legally obligatory”. I make my commitments more precise in the following way: under the legal interpretation (1) of obligatory it holds that acts prescribed by law are obligatory, under the moral interpretation (2) of obligatory it holds that nonperformance of an obligatory act is to be disapproved.’ In schematic form:

(5)
Distinguo!
I replace my commitment .x(∀x->Bx) with the more precise commitment
Int1(.x(∀xÕBx))
I replace my commitment .x(Bx->Cx) with the more precise commitment
Int2(.x(Bx->Cx))

After this move, until further orders, every statement that makes use of ‘Bx’ should be supplied with an index that shows in what way it should be interpreted.

After this move the proponent is no longer in the position any more to accuse the opponent of an inconsistency. The thesis follows only from the reasons when both are read under the same interpretation of ‘obligatory’ and under each interpretation one of the reasons is not accepted by the opponent. So with the Distinguo!-move, the opponent has an effective instrument to counter the strategy of the proponent. Precision is the subject of the next section.
Instead of this move, the opponent can make the further move to accuse the proponent of committing a fallacy by exclaiming Equivocatio!. The burden of proof will consist of explaining why the moves of proponent were fallacious, for example by pointing out which rules of discussion were broken or in what way his arguments were seriously misleading. But it consists in any case of making a distinction in the meaning of an expression used by the proponent. The move Distinguo! is part of a complete defence of the move Equivocatio!. So after each of these moves of the opponent, the proponent needs to be able to counter the distinction if he does not want to lose this line of argumentation.
An easy triumph by the proponent due to the ambiguity of an expression can only be successful if the opponent is deceived and does not make a distinction. Most authors locate the capacity of an argument to mislead in this way in the ambiguity of an expression. The proponent expresses two different things, but the opponent does not notice, because these different things are indicated by the same words.
But there is a difference in the examples mentioned above. It is hardly imaginable that someone will be trapped by example (1), but it is imaginable that one is trapped by example (2). This capacity to mislead explains the realistic character of the latter. I will contend that the ambiguity in realistic examples is of a different nature than in didactic examples. The potential to mislead has a semantic explanation. The difference between both kinds of ambiguity can be explained by means of the notions ‘precization’ and ‘specificity’.

3. Precizations
Manfred Pinkal presented in Logic and Lexicon (Pinkal 1995) a theory for reasoning with ambiguous and vague expressions. The central ideas of this book are very suitable for modelling the problem of ambiguity in discussions. I adopt his notion of a precisification in a slightly different form for the purpose of this paper and call it, like Naess (Naess 1966: 38), a precization.

Imagine a context of utterance where two persons, S and L, are talking about ships. S utters the following ambiguous statement, whereas L evaluates the different precizations (relevant and more precise interpretations) of this statement.

(6)
S: The Santa Maria was a fast ship.
L: Fast? If you mean ‘fast compared to a modern sailboat’, then I do not agree. The Santa Maria was not fast compared to a modern sailboat, not in the actual sense, nor in the dispositional sense of the word. If you mean ‘fast for a 15th century ship’, then it depends. I think the Santa Maria was fast in the dispositional sense of the word, but, actually, she had to sail slowly because the accompanying ships were much smaller. So one statement (0) is given six precizations:

0: The Santa Maria was fast.
P1: The Santa Maria was fast compared to a modern sailboat.
P2: The Santa Maria was actually fast compared to a modern sailboat.
P3: The Santa Maria was dispositionally fast compared to a modern sailboat.
P4: The Santa Maria was fast for a 15th century ship.
P5: The Santa Maria was actually fast for a 15th century ship.
P6: The Santa Maria was dispositionally fast for a 15th century ship.
The set of precizations is dependent on the context of utterance. If S and L were talking about 15th century ships the possible interpretation of ‘fast’ as ‘fast compared to a modern sailboat’ would not be relevant.

But in a more general context of utterance, the above conversation about ships for example, L sees six ways to interpret the statement of S. In precizations P2 and P3 the statement is unacceptable. Since those are the only relevant further precizations of the statement in precization P1, the statement in precization P1 is unacceptable too. The statement in precization P4 has two further precizations, of which one, P5, is unacceptable and one, P6, is acceptable. The statement in precization P4 is therefore neither fully acceptable, nor fully unacceptable, but indefinite. The same applies to statement 0 itself. Because statement (0) does not admit of only acceptable, nor of only unacceptable precizations, it is neither fully acceptable or unacceptable itself, but indefinite.
A statement that is indefinite in a context can also be called too imprecise for that context. A statement that admits of only acceptable or of only unacceptable relevant precizations in a context can be called precise enough for that context. The notion of precision is tied up to particular contexts of utterance, so total precision does not need to bother us.
In accordance with the above terminology a statement (in a certain context) gets the value ‘A’ (acceptable) if it is acceptable in all relevant senses in that context of utterance, the value ‘NA’ (not acceptable) if it is unacceptable in all relevant senses in the context of utterance. A statement gets a third value, designated with ‘I’ if there is a relevant interpretation in the context of utterance under which the statement gets ‘A’ as well as a relevant interpretation under which it gets ‘NA’.

So, by the transitivity of ‘is an interpretation of’, a precization w of i never admits of an interpretation that i does not admit. To keep the definition simple the relation here defined is not the ‘more precise than’ relation, but the ‘at least as precise as’ relation. The practical function of course is to exclude interpretations.

5. Ambiguity in the narrow sense and polysemy
With the notion of ‘precisification’ Pinkal classifies a wide range of linguistic phenomena that can lead to indefiniteness. For this paper it is enough to use a less subtle classification of ambiguity than he does.
When we use the notion of precization to denote parts of sentences, we can say that the word ‘bank’ admits of two standard precizations: ‘edge of a river’ and ‘financial institution’. But when this word is used, it is always in the one or the other specific meaning of ‘bank’. It does not have a potential to mislead. That’s why the linguistic ambiguity test is effective. Put an expression like ‘bank’ in a sentence of the following form ‘That biologist is working on a bank, just as Duisenberg.’ When it is not possible to precizate ‘bank’ to one of the precizations, without feeling that something is wrong with the sentence, the expression is ambiguous. There is, except for some special contexts (Geeraerts 1993: 245), no widest reading (Pinkal 1995: 78) that allows a listener to interpret the expression in a general sense that includes financial institutions and edges of rivers. I call this type of ambiguity ‘ambiguity in the narrow sense’.
When the linguistic ambiguity test is applied to ‘obligatory’ there is not such a strong feeling of awkwardness: ‘Waiting for a red traffic-light is obligatory, just as helping someone in need.’ This type of ambiguity is called polysemy. A listener, eager for distinctions, will point to the difference between the legal and the moral senses of ‘obligatory’, but polysemous expressions do allow for a widest reading. The sentence admits a natural precization without awkwardness: ‘Waiting for a red traffic-light is obligatory in a general sense, just as helping someone in need.’ The word ‘obligatory’ has three different precizations: (P1) ‘morally prescribed’, (P2) ‘legally prescribed’ and (P3) ‘prescribed (legally or morally)’. The meanings of P1 and P2 are semantically strongly related. P3 is the widest reading of the expression that is unspecific towards P1 en P2. That means that in the case of these one-place predicates that the positive extensions of both P1 and P2 are included in the positive extension of P3. So polysemous statements allow for specific precizations and at least one unspecific precization, all precizations being equally precise. So being more precise is not the same as being more specific (Naess 1966: 42). A  user of a polysemous expression could have intended something general.
When the fallacy of equivocation is treated (Freeman 1988: 111-120, Walton 1996: 37-76) the more realistic examples make use of polysemous expressions and not of ambiguous expressions in the narrow sense. This can be explained as follows. Non-realistic examples are non-realistic because it is not imaginable that the listener does not notice that two senses of the expression are being used. The potential of narrow sense ambiguity to mislead within one sentence is minimal, as we saw with the linguistic ambiguity test. The potential to mislead in the broader context of an argument is also very small. That’s why they are used in didactic examples of equivocation. The reader notices immediately that something is wrong. So the author has to explain only what is wrong.
Not only does a polysemous expression designate several meanings, but the specific meanings themselves are so similar that they allow for a widest reading. So if an opponent is mislead by a polysemous expression this can be explained by the fact that not only two meanings are designated by one word, but also by the fact that those two meanings are similar to each other. The opponent can get confused by mixing up different but similar meanings.

6. The seeming correctness of argumentation
A fallacy was traditionally regarded as “an argument that seems to be valid but is not so” (Hamblin 1970:12). In the modern theory of argumentation (Walton & Krabbe 1995, Walton 1996) the distinction between what it seems and what it really is keeps to plays a role in the conception of fallacy. A characteristic for many fallacies is that they could be reasonable arguments in some type of context but that they are not reasonable in the context wherein they are actually used. That gives the argumentation a semblance of reasonableness that is able to deceive a discussionpartner.
The seeming correctness of an equivocation can be explained by pointing at the nature of polysemy. The semantical similarity relation between the different possible precizations, specific and unspecific, explains the persuasive power of the terminology.

7. Discussion-techniques
The opponent can not only precizate her commitments to commitments that are more precise and more specific, but she also has the possibility to make her commitments precise but unspecific. This is a variant of the Distinguo!-move that is seldom pointed at, probably because the notions of preciseness and specificity are often not clearly separated. For now, I will discuss only the Distinguo!-move I described in section 2:

(5)
Distinguo!
I replace my commitment .x(Ax->Bx) with the more precise commitment
Int1(.x(Ax->Bx))
I replace my commitment .x(Bx->Cx) with the more precise commitment
Int2(.x(Bx->Cx))

What possibilities are there for the proponent at the next stage of the discussion? I will describe some plausible moves, skipping the possibility of giving up this line of argumentation or abandoning the discussion altogether.

A. The proponent can choose one of the interpretations of ‘obligatory’, for example interpretation 2, and check which of the reasons is not yet accepted in that interpretation by the opponent. The proponent defends that reason in interpretation 2. The same is possible for a choice for interpretation 1.

(7)
Under the moral interpretation of ‘obligatory’ it holds that acts prescribed by law are obligatory, in schematic form:
Int2(_x(∀x_Bx)).
Under the legal interpretation of obligatory it holds that nonperformance of an obligatory act is to be disapproved, in schematic form:
Int1(.x(Bx->Cx)).

Both possibilities imply that the proponent accepts the distinction and that he wants to try to convince the opponent that for one of the precizations both reasons are acceptable under that interpretation. If the proponent would succeed, he once again can confront the opponent with the inconsistency between her adherence to the commitments and her critical attitude towards the thesis.

B. The proponent can attack the relevance of the distinction by claiming that both reasons should be acceptable under all precizations. Since the opponent already committed herself to two of the required statements, the proponent brings forward the other two: Int2(.x(∀x->Bx)) and Int1(.x(Bx->Cx)).
With this move he tries to neutralize the distinction. If the opponent eventually accepts all reasons in all relevant precizations, both parties may henceforth use expression ‘obligatory’ without mentioning which precization is intended.

C. The proponent can appeal to the unspecific precization of his reasons. He can explain that the opponent is wrong in neglecting the general interpretation. He explains that he meant obligatory in general, legally or morally, and asks the opponent to consider if the reasons are acceptable to her under that precization. In schematic form: Int3(.x(∀x->Bx)) and Int3(.x(Bx->Cx)). The proponent will probably have to defend the second reason that now reads: ‘nonperformance of an act that is either morally or legally obligatory is to be disapproved.’

D. Walton (Walton 1987: 255) discusses the further option where an extreme legal positivistic proponent defends himself by saying that he meant ‘legally and obligatory’, because moral obligation and legal obligation are the same thing. In schematic form:
Int4(.x(∀x->Bx)) and Int4(.x(Bx->Cx)). This could be a specific precization, but in the present case it is not an interpretation standard in ordinary English (so perhaps violating clause (1) of the definition of ‘precization’). The proponent could of course stipulate this meaning for this discussion. He will then probably have to defend the first reason that now reads: ‘actions prescribed by law are both legally and morally obligatory’.

E. In special cases the proponent can appeal to a meaning postulate. The case in question is not suitable to illustrate this kind of move, so I take a different case. In the following discussion the opponent makes the wrong choice in precizating her commitments. She should not be able to get away with it. So the proponent must be able to appeal to relations between meanings expressed in meaning postulates.

(8)
Proponent: Donald is a duck. Ducks are female.
Opponent: I admit this.
Proponent: So Donald is female.
Opponent: Distinguo! I precizate my commitment ‘Donald is a duck’ to ‘Donald is a duck in the specific sense of ‘duck’’ and precizate my commitment ‘Ducks are female’ to ‘Ducks in the general sense of duck are female’.
Proponent: There is a meaning postulate for ‘duck’ that says ‘if x is a duck in the specific sense than x is a duck in the general sense.’ You committed yourself to ‘Donald is a duck in the specific sense, so you should commit yourself to ‘Donald is a duck in the general sense.’ You also committed yourself to ‘Ducks in the general sense of duck are female’. So you should accept my thesis.

The use of meaning postulates by the proponent prevents the opponent of winning an easy triumph with a non-sensible Distinguo!.

F. The proponent can make a counter-distinction. Such a move can be directed towards an expression that has not yet been the subject of an earlier distinction, but it can also be directed towards the expression the opponent already submitted to a distinction. An example of the first possibility.

(9)
Proponent: You are right, nonperformance of a legally obligatory act is not to be disapproved, in the strict moral sense of ‘disapproved’. But nonperformance of a legally obligatory act is to be disapproved in a general sense of ‘disapproved’.

In schematic form: Distinguo! I precizate Int1(.x(Bx->Cx)): not Int1.1(.x(Bx->Cx)) but Int1.2(.x(Bx->Cx)).

An example of the second possibility.

(10)
Proponent: You are right, it’s not the case that acts prescribed by law are morally obligatory, in the sense of moral that you should do what is morally minimal. But it is the case that acts prescribed by law are morally obligatory, in the sense of moral that you should do what is morally maximal.

In schematic form: Distinguo! I precizate Int2(.x(∀x_Bx)): not Int2.1(.x(∀x->Bx)) but Int2.2(.x(∀x->Bx)).

These distinctions in reaction to another distinction are very much like Reschers countermoves to distinctions (Rescher 1977: 15), but here they are especially related to the use of language and not restricted to presumptive reasoning.

8. The evaluation of ambiguity in argumentation.
It is polysemy rather than ambiguity in the narrow sense that has the potential to mislead in a discussion. My first point therefore is that the seeming correctness of an argument that one wants to qualify as fallacious, can be explained by the similarity of the meanings of a polysemous expression.
As already said, within a dialectical approach, an argument should be evaluated relative to an opponent with a specific set of commitments. It is perfectly possible to imagine an opponent who does not make a difference between legal and moral prescriptions. In this situation, the argument contains a polysemous expression, but the expression is precise enough for this situation. For this opponent will probably accept the statements containing the polysemous expression in all precizations. My second point is that the occurrence of polysemy does not always indicate a lack of precision.
But relative to the opponent we imagined throughout the paper, the proponent is too imprecise, whether the opponent notices it or not. After she notices it and makes a Distinguo!-move or Equivocatio!-move the proponent has not yet lost this line of argumentation. We have seen that the proponent has possibilities to go on within the line of argumentation he started, for example by defending both reasons under one specific or unspecific precization of ‘obligatory’. It is even possible that the proponent accepts the meaning distinction and submits it to a further distinction. So my third point is that lack of precision relative to an attentive opponent does not imply that the discussion is blocked. In the examined case the proponent could combine two possible moves in the following way.

Proponent: I intended ‘obligatory’ in both reasons in the general sense of ‘morally or legally obligatory’. And I did not mean ‘disapprove’ in the strict moral sense, but also in the general sense of ‘morally or legally disapprove’.

So the proponent can make his own reasons more precise with unspecific precizations. My fourth point is that distinctions and precision should not be mixed up with specificity.

What in the beginning was presented as an example of a fallacy, now turns out to be an argument that does not have to block the course of the discussion. Furthermore it is possible that it is capable of being reasonably defended by the proponent. I represented the moves by proponent and opponent without mentioning any discussion rules, but as I see it, none of the represented moves contains a clear violation of a rule of an ideal model for discussion. So my fifth point is that example (2) (just as the first example for not being misleading) is not a straightforward example of a fallacious argument. To present it as an example of the fallacy of equivocation it should be placed in a context where the proponent lacks any reasonable defence relative to his opponent.

REFERENCES
Crawshay-Williams, R. (1957). Methods and Criteria of Reasoning: An Inquiry into the Structure of Controversy. London: Routledge and Kegan Paul.
Eemeren, F.H. van & R. Grootendorst (1992). Argumentation, Communication and Fallacies: a Pragma-Dialectical Perspective. Hillsdale: Lawrence Erlbaum Associates.
Freeman, J.B. (1988). Thinking Logically: Basic Concepts for Reasoning. New Jersey: Prentice Hall.
Geeraerts, D. (1993). Vagueness’s puzzles, polysemy’s vagaries. Cognitive Linguistics, 4, 223-272.
Hamblin, C.L. (1970). Fallacies. Virginia: Vale Press.
Mackenzie, J. (1988). Distinguo: the response to equivocation. Argumentation, 2, 465-482.
Mackenzie, J. (1989). Four Dialogue Systems. Studia Logica, 17, 567-583.
Naess, A. (1953). Interpretation and Preciseness. A Contribution to the Theory of Communication. Oslo: Grøndahl & Søns Boktrykkeri.
Naess, A. (1966). Communication and Argument: Elements of Applied Semantics. Oslo: Universiteitsforlaget.
Pinkal, M. (1995). Logic and Lexicon: The Semantics of the Indefinite. Dordrecht: Kluwer Academic Publishers.
Rescher, N. (1977). Dialectics: A Controversy-Oriented Approach to the Theory of Knowledge. New York: SUNY Press.
Walton, D. (1987). Informal Fallacies: Towards a Theory of Argument Criticisms. Amsterdam: John Benjamins Publishing Company.
Walton, D. & E.C.W. Krabbe, (1995). Commitment in Dialogue: Basic Concepts of Interpersonal Reasoning. New York: SUNY Press.
Walton, D. (1996). Fallacies Arising from Ambiguity. Dordrecht: Kluwer Academic Publishers.