ISSA Proceedings 2002 – I Don’t Have Anything To Prove Here – The (Un)Reasonableness Of Evading The Burden Of Proof

• by: F.H. van Eemeren, B. Garssen & B. Meuffels - University of Amsterdam

1. Those who affirm must prove
Critical decision making, be it about future plans and policies or facts and theories often takes place in the context of on argumentative discussion in which two parties try to reach a decision. In the pragma-dialectical argumentation theory, the various moves made in argumentative discourse are seen as part of critical discussion aimed ad resolving a difference of opinion concerning the acceptability of a claim or standpoint. The moves made by the parties involved, are regarded reasonable only if these are a contribution to the resolution of the difference. In an ideal model of a critical discussion the rules are specified that an exchange of discussion moves has to comply with to further the resolution. The soundness of the pragma-dialectical rules is based on their problem validity: the fact that they are instrumental in resolving a conflict. To resolve a difference of opinion however, the rules must also be acceptable to the parties involved. That means they should be intersubjectively approved.
That is why it is important to know what ordinary language users think of discussion moves that are deemed fallacious by the pragma-dialectical theory. In a comprehensive research project, we systematically try to find out if the theoretical norms are in accordance with the norms ordinary language (claim to) apply when judging argumentation. In this paper we would like to present the results of a study on the rule concerning the burden of proof.
In everyday discussions many things can go wrong. Some discussions hardly start, and others derail totally. Sometimes it goes wrong before the arguers put forward only one argument. For example, when one participant openly tries to disqualify his opponent by calling him stupid, untrustworthy or biased. An early obstruction of a discussion is also possible when the opponents cannot decide who has to defend his of her position. In principle the rule that ever since antiquity is supposed to be valid is pretty clear: who asserts must prove.
By virtue of this rule, the party who puts forward a standpoint has to defend that standpoint by means of argumentation. In spite of the relative simplicity of the rule, in practice all kinds of things can go wrong with the distribution of the burden of proof.

For all the stages in a critical discussion, specific rules apply that should guarantee the resolution of the conflict. A violation of a rule by one of the contesters frustrates or blocks the resolution of the difference of opinion. In the pragma-dialectical argumentation theory such a violation is seen as a false discussion move or a fallacy. What do ordinary language users think of such ‘false’ moves? Do they also think they are fallacious? Are they always fallacious? A series of experimental studies about ordinary language users’ norms indicates that ordinary language users indeed think that the traditional fallacies are unreasonable discussion moves (Van Eemeren & Meuffels 2002: 58). In that respect their pre-theoretical norms agree with the pragma-dialectical norms. This research however was restricted to the first pragma-dialectical rule: the so called freedom rule, which claims that every party in the discussion should be free to advance his standpoint or casting doubt on standpoints. The fallacies that have been studied so far are typical for the confrontation stage of a critical discussion such as the argumentum ad hominem and the argumentum ad baculum.

In the opening stage the parties decide to make an attempt to solve the difference of opinion: they make agreements about how are they going to proceed during the discussion, about the starting point of discussion – i.e. what are the concessions of both the parties that constitute the common grounds – and about the divisions of roles: Who is going to be the defender of the standpoint, the protagonist, and who is going to be the attacker of the standpoint- the antagonist. The rule for the opening stage which is known as the pragma-dialectical burden of proof rule is as follows: ‘A party who puts forward a standpoint is obliged to defend it if asked to do so’ (Van Eemeren & Grootendorst 1992: 117). This rule can be violated in a number of ways. For now we focused on one particular violation of the burden of proof rule. What happens when both parties in a discussion put forward a standpoint about a certain issue and one of the parties simply refuses to defend his own standpoint? According to the pragma-dialectical rule this is clearly fallacious. Do language users agree with this rule? Do they always agree or are there circumstances in which their judgments divert?

2. Shifting the burden of proof in non-mixed disputes
The term burden of proof comes from the field of law and refers to the obligation to prove the correctness or plausibility of certain facts. Unlike in every day life discussions, in procedural law there are specific rules for the division of the burden of proof. In case the rules are missing, the judge can decide.
Historically speaking the term ‘burden of proof’ stems from classical Roman Law in which this ‘burden’ (i.e. task; assignment, obligation) to defend one case was known as the onus probandi. This notion was related to the fundamental and legally established division of roles between prosecutor and defender in the process. The onus probandi regulated the procedural question which party should come when with evidence. Under Roman law, in all cases the prosecutor had to start by stating his case. Next, he had to put forward argumentation to defend his case. Subsequently the defender had to defend his counter case in the so-called exceptio. The prosecutor could react to the counter case in the replicatio. In short, the burden of proof lay in each case with the party who made the accusation (Rescher 1977: 25). The basis rule was: ‘necessitas probandi incumbit ei qui dicit not ei qui negat’ (‘the obligation or onus to provide evidence lays with him who claims not with him who denies the claim’)

The parties in an every day life argumentative discussions are free to arrange the distribution of the burden of proof. According to the pragma-dialectical discussion model the parties first put forward their standpoints in the confrontation stage and make arrangements for the distribution of the burden of proof in the opening stage. It is possible that the parties agree to an arrangement according to which the party who initially doubted the standpoint agrees to defend while the party who put forward the standpoint attacks it. According to Van Eemeren and Grootendorst such an agreement to play the Devil’s advocate can actually foster the critical testing of the standpoint (Van Eemeren & Grootendorst 1984: 162).

However, in a normal situation in which the parties do not explicitly agree on the distribution of the burden of proof, they may take it that the burden of proof lies with the party who put forward a standpoint. In the simplest situation there is a non-mixed dispute in which only one party puts forward a standpoint, while the other party just doubts the standpoint. In this case the burden of proof lies with the party who claims. In a more complex case there is a mixed dispute in which both parties put forward a standpoint on one issue. The one party claims that the proposition is acceptable while the other party thinks it is not acceptable is not acceptable. In this situation both parties have the burden of proof and therefore there are two positions to defend.

In practice parties sometimes try to escape from the burden of proof by simply putting it on the shoulders of the other party. This is called the fallacy of shifting the burden of proof. The protagonist shifts the burden of proof in a non-mixed dispute if he challenges his opponent to defend the opposite of the original standpoint, like in the following example:
A: Journalists get more subjective every day.
B: How come?
A: Well, maybe you can explain that they are as objective as they used to be.

A puts forward a standpoint in the confrontation stage, while B casts doubt on that same standpoint. In the normal case B is only challenger and has nothing to defend; the burden of proof clearly lies with A. B is being saddled with the role of protagonist of the contrary standpoint. This move is of course only successful if B is willing to take that role and to defend his standpoint. A knows that B’s possible failure to defend his standpoint will be to his own advantage.
Our earlier experimental studies show that ordinary language users in general think that the fallacy of shifting the burden of proof is highly unreasonable. In our research the respondent had to judge moves in short argumentative exchanges. We have strong indications that our respondents adhere to the pragma-dialectical burden of proof rule at least in respect of the fallacy of shifting the burden of proof (Van Eemeren et al. 2000).
Shifting the burden of proof however is not the only violation of the burden of proof rule. It is also possible for the protagonist to evade the burden of proof. One way of doing that is to present the standpoint in such a way that there is no need to defend it in the first place by giving the impression that there is no point in calling it into question. This can be done by presenting the standpoint as self-evident and using formulations such as: ‘It is clear that…’, and ‘It goes without saying that…’. Another way is to give a personal guarantee of the acceptability of the standpoint and using formulations such as ‘I can assure you…’, ‘You can take it from me that…’ or ‘It is my personal conviction that…’. This kind of move is powerful because it leaves the opponent with two options: accept the standpoint or openly abandon faith in the protagonist.
A third way of evading the burden of proof is to formulate the standpoint in such a way that is protected from any critical assessment. This can be done by using ‘hermetic’ wordings and leave out articles, as in ‘Germans are essentially war mongers’ or ‘By nature women are nosy’. These formulations are fallacious because critical attacks will bounce of on an armor of immunity.

So far, these violations of the burden of proof rule can occur in simple non-mixed disputes. In more complex cases the parties in the discussion try to evade the burden of proof in mixed disputes. In a mixed dispute both parties in the discussion put forward a standpoint. One party claims that smoking is bad for your health while the other party claims that smoking is not bad for your health. Since there are two opposing standpoints, the dispute is of the mixed type. In a mixed dispute the default situation is that both parties have the obligation to defend their own standpoint. The question is: who will start; what will be the order of defense?
In the ideal model for critical discussions this problem of order is dealt with in the opening stage. In their decision-making, the parties can use the principle that the initiator of the discussion topic should start. This principle at least follows the conversational standard sequential of standpoint-argumentation-rejection/acceptance. Another rule of thump that can be helpful in deciding which party goes first is the principle that the party who comes up with a new plan should start defending this plan. Or the party who attacks a generally accepted belief or opinion should start.

The problem of order can in principle be solved and when both parties agree it is not an obstacle of the process of conflict resolution. In practice it becomes troublesome when a party presents the problem of order as a problem of choice. The party who commits this fallacy lays the burden of proof solely on his opponents’ side and denies any burden or commitment.
In fact, the arguer who commits this fallacy appeals to the principle of status quo. Just as in criminal law the party who wishes to change the status quo has the burden of proof. This means that the status quo has the status of presumption. Going against the status quo means proposing a new plan or policy or attacking a commonly accepted belief or opinion. However, in all of these cases both parties in the mixed dispute have the burden of proof for their own position irrespective of the type of standpoint[i].
Also, when it is impossible for one of the parties to defend his position because he has not access the required information it would be senseless to lay the burden of proof with this party. Because one of the parties cannot provide the necessary proof for his standpoint the parties should agree in the opening stage that for now the burden of proof lies only with one or the parties. This situation is typical for accusations. When for instance in an every life dispute A accuses his fiancée B of cheating on him, it will be very hard for B to prove the opposite. That means that B should not have the burden of proof for her standpoint that she did not cheat. However B is obliged and also has the right to refute the arguments that A puts for forward.

A: You cheated on me.
B: No, I certainly did not.

In our empirical study we want to find you whether the norms ordinary language users (claim to) apply when evaluating argumentation, are in agreement with these theoretical norms. How reasonable or unreasonable is the fallacy of evading the burden of proof in the eyes of naïve judges? Furthermore, we wanted to know whether the type of standpoint influences their opinions about this fallacy. Is, for instance, evading the burden of proof seen as less unreasonable when one is defending commonly accepted opinions or when one is defending the status quo against new proposals for change?

3. Experimental design
In our experimental study we used 32 argumentative dialogues. Each dialogue consisted of 2 turns and was preceded by a short situation sketch in which the parties were introduced and the dispute itself became clear. It was made clear to the respondents exactly what party put forward what standpoint. Only one thing we avoided to reveal: the order of standpoint presentation. The question who started the discussion was left open if possible. The respondents could be tempted to think that the person who started the discussion should start defending his standpoint. And that is what we tried to avoid.

In 16 of the dialogues party B claims that he has nothing to proof and that the opponent should proof his position. In 4 of those dialogues the last move is not fallacious at all because the issue is an accusation and it seems impossible for the defender to proof his innocence. As in the following example:
Robert and Anita are having an argument. Anita claims that Robert cheated on her. Robert denies the accusation.
Anita: Proof that you didn’t cheat on me.
Robert: No, I have nothing to proof. You should proof that I did not cheat on you.

In another 4 dialogues the discussion is about a proposed plan. Speaker B fallaciously lays the burden of proof with the order party and evades the burden of proof. As in the following dialogue:
Eric thinks that it would be good to increase the maximum speed limit to 150 kilometers an hour. Peter thinks that it is not necessary and that we should leave it at 120.
Eric: Why should we leave it at 120?
Peter: No, you should explain to me why it should be 150.

Again in another 4 dialogues the discussion is about an alleged fact. We made sure that the standpoint was a commonly accepted belief or opinion. In a pilot research we checked our intuitions on this point.
John says that in general it is easier for Dutch high school students to learn French than English. Ellen thinks that that is nonsense. She believes that English is in fact much easier to learn.
John: Why do you think English is easier to learn?
Ellen: Why do I have to explain that? You tell me why you think French is easier.

In the last 4 episodes we constructed discussions about neutral standpoints: in these cases the positions did not go against the status quo.
The members of a political party are having a discussion about the question whether Adams is suitable for parliament. Mrs.Van Dyck things Adams is not suitable while Mr. Williams thinks Adams is suitable.
Williams: Why do you think Adams is not suitable?
Van Dyck: Why do I have to explain that? You should tell us why you think he is suitable.

As before one of the parties claims he has nothing to prove and fallaciously lays the burden of proof with his opponent. As can bee seen in the examples we tried to use quite resolute formulations to make sure that respondents understand that the burden of proof is distributed to one side only.
The rest of the 32 dialogues were meant as fillers in the experiment. 10 of those were unproblematic reasonable, non-fallacious dialogues. To avoid alternative explanations in these non-fallacious dialogues we use the same kind of resolute formulations as we used in the fallacious dialogues.
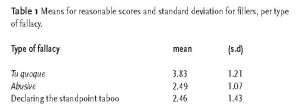
For reasons of comparison we also included fallacious dialogues we used in earlier studies. Those include two types of ad hominem attacks and the fallacy of declaring the standpoint taboo. We changed the formulation of these fallacies to let them look like our experimental items. Because we know what is to be expected this addition provides a good stability check.
A total of 70 (17 to 18 year old) Dutch high school students took part in the test. None of the respondents received any special schooling in argumentation theory. The respondents were to express their judgments on a 7-point scale (1= very unreasonable, 7 = very reasonable). In all cases the respondents had to judge the dialogue turn of the last speaker[ii].

4. Results
Table 1 shows the results for the fillers. These results as to results we found in our previous studies (cf. Van Eemeren et al., 19. That means the respondents reacted in a normal way and that there are probably no sample mistakes.

Table 1: Means for reasonable scores and standard deviation for fillers, per type of fallacy

The judgments about the reasonable dialogues are in accordance with what can be expected as well. The mean proves to be almost 5.7 (s.d.=.55) Given the fact that we used a seven-point scale, we may take it that the respondents evaluated these dialogues as reasonable in an absolute sense.

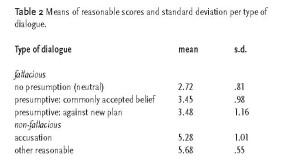
Discussion moves containing a fallacy of the evasion of the burden of proof are seen as unreasonable in an absolute sense, regardless whether the standpoint at issue had a presumptive status or not (see Table 2).

Table 2: Means of reasonable scores and standard deviation per type of dialogue

A further analysis reveals that the respondents did not differentiate between reasonable dialogues and dialogues containing accusations. In that respect the respondents reacted in accordance with the pragma-dialectical burden of proof rule. The discussion moves that contained a fallacy of evading the burden of proof were all considered as unreasonable in an absolute sense. Those results are also in accordance with the burden of proof rule.

The respondents – as was more or less expected – discriminated between the unreasonableness of the three types of violations. The fact that a standpoint has a presumptive status plays a role in their judgments. Evasion fallacies in case of commonly accepted beliefs are equally unreasonable but the respondents are less unreasonable than evasion fallacies in case there is a neutral standpoint.

In other words: the fallacy of evading the burden of proof is considered unreasonable no matter what kind of standpoint. But respondents are less strict in their judgments when the violator has the presumption on its side.

5. Conclusion
Language users make a sharp difference between fallacious and non-fallacious discussion moves; fallacious discussion moves are found to be much more unreasonable than reasonable discussion moves. The subjects were able to detect violations of the burden of proof rule. Also, presumption proves to play an important role in their judgments about the fallacy of evading the burden of proof. The paradigmatic case of presumption (the presumed innocence of the accused in a criminal cases) proves to be taken by the subjects just as was expected from a normative-theoretical viewpoint: in the eyes of language users, the accused who is not in the position to prove his innocence may put the burden of proof on the opposition.

NOTES
[i] There are a few exceptions to this rule. When the parties have argued about the same standpoint and nothing changed, it would be senseless to have the same discussion again, because the exact same outcome may be expected.
[ii] We split the total group of respondents into two subgroups; one group received dialogues in which the evasion of the burden of proof was explicitly motivated (I don’t have to prove my position because you propose a new plan), the second group received dialogues without such an explicit motivation. There proved to be no significant differences between these two groups.

REFERENCES
Eemeren, F.H. van & R. Grootendorst (1984). Speech acts in argumentative discussions: a theoretical model for the analysis of discussions directed towards solving conflicts of opinion. Dordrecht, Holland ; Cinnaminson, U.S.A.: Foris Publications.
Eemeren, F.H. van & R. Grootendorst (1992). Argumentation, Communication, and Fallacies. A Pragma-Dialectical Perspective. Hillsdale, N.J.: Lawrence Erlbaum.
Eemeren, F.H. van, B. Garssen & B. Meuffels (2000). Oordelen over het verschuiven van de bewijslast. In R. Neutelings, N. Ummelen & A. Maes (red.) Over de grenzen van de taalbeheersing; Onderzoek naar taal, tekst en communicatie. (129-140). Den Haag: SDU.
Eemeren, F.H. van, B. Garssen & B. Meuffels (2001). The unreasonableness of the ad baculum fallacy. In: G.T. Goodnight (ed.). Arguing communication and culture. Selected Papers from the Twelfth NCA/AFA Conference on Argumentation. (pp. 343-350). Washington: NCA.
Rescher, N. (1977). Dialectics : a controversy-oriented approach to the theory of knowledge. Albany: State University of New York Press.

You May Also Like

ISSA Proceedings 2006 ~ The Criminal Abduction Paradox

ISSA Proceedings 2006 ~ A Discussion Of Habermas’ Reading And Use Of Toulmin’s Model Of Argumentation

ISSA Proceedings 2006 ~ The Rules Of The Critical Discussion And The Development Of Critical Thinking

ISSA Proceedings 2006 ~ An Analysis Of Preschool Hebrew Speaking Children’s Arguments From The Perspective Of The Pragma-Dialectical Model

ISSA Proceedings 2006 ~ Putin’s Terrorism Discourse As Part of Democracy And Governance Debate In Russia

ISSA Proceedings 2006 ~ Cultural Differences In The Persuasiveness Of Normatively Strong And Normatively Weak Expert Evidence

Comments