ISSA Proceedings 2010 – Argumentation Without Arguments

1 . Introduction
A well-known ambiguity in the term ‘argument’ is that of argument as an inferential structure and argument as a kind of dialogue. In the first sense, an argument is a structure with a conclusion supported by one or more grounds, which may or may not be supported by further grounds. Rules for the construction and criteria for the quality of arguments in this sense are a matter of logic. In the second sense, arguments have been studied as a form of dialogical interaction, in which human or artificial agents aim to resolve a conflict of opinion by verbal means. Rules for conducting such dialogues and criteria for their quality are part of dialogue theory.

Both logic and dialogue theory can be developed by formal as well as informal means. This paper takes the formal stance, studying the relation between formal-logical and formal-dialogical accounts of argument. While formal logic has a long tradition, the first formal dialogue systems for argumentation where proposed in the 1970s, notably by the argumentation theorists Hamblin (1970,1971), Woods & Walton (1978) and Mackenzie (1979). In the 1990s AI researchers also became interested in dialogue systems for argumentation. In AI & Law they are studied as a way to model legal procedure (e.g. Gordon, 1995; Lodder, 1999; Prakken, 2008), while in the field of multi-agent systems they have been proposed as protocols for agent interaction (e.g. Parsons et al., 2003). All this work implicitly or explicitly assumes an underlying logic. In early work in argumentation theory the logic assumed was monotonic: the dialogue participants were assumed to build a single argument (in the inferential sense) for their claims, which could only be criticised by asking for further justification of an argument’s premise or by demanding resolution of inconsistent premises. AI has added to this the possibility of attacking arguments with counterarguments; the logic assumed by AI models of argumentative dialogues is thus nonmonotonic. Nevertheless, it is still argument-based, since counterarguments conform to the same inferential structure as the arguments that they attack.

However, I shall argue that formal systems for argumentation dialogues are possible without presupposing arguments and counterarguments as inferential structures. The motivation for such systems is that there are forms of inference that are not most naturally cast in the form of arguments (e.g. abduction, statistical reasoning or coherence-based reasoning) but that can still be the subject of argumentative dialogue, that is, of a dialogue that aims to resolve a conflict of opinion. This motivates the notion of a theory-building dialogue, in which the participants jointly build some inferential structure during a dialogue, which structure need not be argument-based. Argumentation without arguments is then possible since, even if the theory built during a dialogue is not argument-based, the dialogue still aims to resolve a conflict of opinion.

This paper is organized as follows. In Section 2 the basics are described of logics and dialogue systems for argumentation, and their relation is briefly discussed. Then in Section 3 the general idea of theory-building dialogues is introduced and in Section 4 some general principles for regulating such dialogues are presented. In Section 5 two example dialogue systems of this kind are presented in some more detail.

2. Logical and dialogical systems for argumentation
In this section I briefly describe the basics of formal argumentation logics and formal dialogue systems for argumentation, and I explain how the former can be used as a component of the latter. A recent collection of introductory articles on argumentation logics and their use in formal dialogue systems for argumentation can be found in Rahwan & Simari (2009). An informal discussion of the same topics can be found in Prakken (2010).

2.1. Argumentation logics
Logical argumentation systems formalise defeasible, or presumptive reasoning as the construction and comparison of arguments for and against certain conclusions.  The defeasibility of arguments arises from the fact that new information may give rise to new counterarguments that defeat the original argument.  That an argument A defeats an argument B informally means that A is in conflict with, or attacks B and is not weaker than B. The relative strength between arguments is determined with any standard that is appropriate to the problem at hand and may itself be the subject of argumentation. In general, three kinds of attack are distinguished: arguing for a contradictory conclusion (rebutting attack), arguing that an inference rule has an exception (undercutting attack), or denying a premise (premise-attack). Note that if two arguments attack each other and are equally strong, then they defeat each other.

Inference in argumentation logics is defined relative to what Dung (1995) calls an argumentation framework, that is, a given set of arguments ordered by a defeat relation. It can be defined in various ways. For argumentation theorists perhaps the most attractive form is that of an argument game. In such a game a proponent and opponent of a claim exchange arguments and counterarguments to defend, respectively attack the claim. An example of such a game is the following (which is the game for Dung’s 1995 so-called grounded semantics; cf. Prakken & Sartor, 1997; Modgil & Caminada, 2009). The proponent starts with the argument to be tested and then the players take turns: at each turn the players must defeat the other player’s last argument: moreover, the proponent must do so with a stronger argument, i.e., his argument may not in turn be defeated by its target. Finally, the proponent is not allowed to repeat his arguments. A player wins the game if the other player has no legal reply to his last argument.

What counts in an argument game is not whether the proponent in fact wins a game but whether he has a winning strategy, that is, whether he can win whatever arguments the opponent chooses to play. In the game for grounded semantics this means that the proponent has a winning strategy if he can always make the opponent run out of replies. If the proponent has such a winning strategy for an argument, then the argument is called justified. Moreover, an argument is overruled if it is not justified and defeated by a justified argument, and it is defensible if it is not justified but none of its defeaters is justified. So, for example, if two arguments defeat each other and no other argument defeats them, they are both defensible.  The status of arguments carries over to statements as follows: a statement is justified if it is the conclusion of a justified argument, it is defensible if it is not justified and the conclusion of a defensible argument, and it is overruled if all arguments for it are overruled. (Recall that these statuses are relative to a given argumentation framework.)

Argument games should not be confused with dialogue systems for argumentation: an argument game just computes the status of arguments and statements with respect to a nonmonotonic inference relation and its proponent and opponent are just metaphors for the dialectical form of such computations. By contrast, dialogue systems for argumentation are meant to resolve conflicts of opinion between genuine agents (whether human or artificial).

2.2. Dialogue systems for argumentation
The formal study of dialogue systems for argumentation was initiated by Charles Hamblin (1971) and developed by e.g. Woods & Walton (1978), Mackenzie (1979) and Walton & Krabbe (1995). From the early 1990s researchers in artificial intelligence (AI) also became interested in the dialogical side of argumentation (see Prakken 2006 for an overview of research in both areas). Of particular interest for present purposes are so-called persuasion dialogues, where two parties try to resolve a conflict of opinion. Dialogue systems for persuasive argumentation aim to promote fair and effective resolution of such conflicts. They have a communication language, which defines the well-formed utterances or speech acts, and which is wrapped around a topic language in which the topics of dispute can be described (Walton & Krabbe 1995 call the combination of these two languages the ‘locution rules’). The topic language is governed by a logic, which can be standard, deductive logic or a nonmonotonic logic. The communication language usually at least contains speech acts for claiming, challenging, conceding and retracting propositions and for moving arguments and (if the logic of the topic language is nonmonotonic) counterarguments. It is governed by a protocol, i.e., a set of rules for when a speech act may be uttered and by whom (by Walton & Krabbe 1995 called the ‘structural rules’). It also has a set of effect rules, which define the effect of an utterance on the state of a dialogue (usually on the dialogue participants’ commitments, which is why Walton & Krabbe 1995 call them ‘commitment rules’). Finally, a dialogue system defines termination and outcome of a dispute. In argumentation theory the usual definition is that a dialogue terminates with a win for the proponent of the initial claim if the opponent concedes that claim, while it terminates with a win for opponent if proponent retracts his initial claim (see e.g. Walton & Krabbe 1995). However, other definitions are possible.

2.3. The relation between logical and dialogical systems for argumentation
A stated in the introduction, formal dialogue systems for persuasive argumentation assume an underlying logic. In argumentation theory it is usually left implicit but in AI it is almost always an explicit component of dialogue systems. Also, in early work in argumentation theory the logic assumed was monotonic: the dialogue participants were assumed to build a single argument (in the inferential sense) for their claims, which could only be criticised by asking for further justification of an argument’s premise (a premise challenge) or by demanding resolution of inconsistent premises. (In some systems, such as Walton & Krabbe’s (1995) PPD, the participants can build arguments for contradictory initial assertions, but they still cannot attack arguments with counterarguments.) If a premise challenge is answered with further grounds for the premise, the argument is in effect ‘backwards’ extended into a step-by step-constructed inference tree.

Consider by way of example the following dialogue, which can occur in Walton & Krabbe’s (1995) PPD system and similar systems. (Here and below P stands for proponent and O stands for opponent.)
P1: I claim that we should lower taxes
O2: Why should we lower taxes?
P3: Since lowering taxes increase productivity, which is good
O4: I concede that increasing productivity is good,
O5: but why do lower taxes increase productivity?
P6: Since professor P, who is an expert in macro-economics, says so.

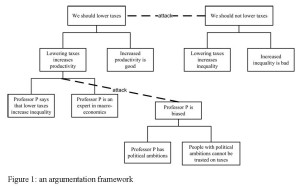
The argument built during this dialogue is the one on the left in Figure 1.

AI has added to this the possibility of counterargument: an argument can in AI models also be criticised by arguments that contradict a premise or conclusion of an argument or that claim an exception to its inference. The logic assumed by AI models of argumentative dialogues is thus nonmonotonic, since new information can give rise to new counterarguments that defeat previously justified arguments. Nevertheless, in most AI models it is still argument-based, since counterarguments conform to the same inferential structure of the arguments that they attack.

In our example, counterarguments could be stated as follows:
O7: But professor P is biased, so his statement does not support that lower taxes increase productivity
P8: Why is professor P biased?
O9: Since he has political ambitions, and people with political ambitions cannot be trusted when they speak about taxes.
O10: Moreover, we should not lower taxes since doing so increases inequality in society, which is bad.

The argument built in O7 and O8 argues that there is an exception to the argument scheme from expert testimony applied in P6, applying the critical question whether the expert is biased (this paper’s account of argument schemes is essentially based on Walton 1996). A second counterargument is stated at once in O10, attacking the conclusion of the initial argument. Both arguments are also displayed in Figure 1.

 

3. Theory building dialogues
Now it can be explained why the inferential structures presupposed by a dialogue system for persuasion need not be argument-based but can also conform to some other kind of inference. Sometimes the most natural way to model an inferential problem is not as argumentation (in the inferential sense) but in some other way, for example, as abduction, statistical reasoning or coherence-based reasoning. However, inferential problems modelled in this way can still be the subject of persuasion dialogue, that is, of a dialogue that is meant to resolve a conflict of opinion.  In short: the ‘logic’ presupposed by a system for persuasion dialogue can but need not be an argument-based logic, and it can but need not be a logic in the usual sense.

This is captured by the idea of theory-building dialogues. This is the idea that during a dialogue the participants jointly construct a theory of some kind, which is the dialogue’s information state at each dialogue stage and which is governed by some notion of inference. This notion of inference can be based an argumentation logic, on some other kind of nonmonotonic logic, on a logical model of abduction, but also on grounds that are not logical in the usual sense, such as probability theory, connectionism, and so on. The dialogue moves operate on the theory (adding or deleting elements, or expressing attitudes towards them), and legality of utterances as well as termination and outcome of a dialogue are defined in terms of the theory.

4. Some design principles for systems for theory-building persuasion dialogues
I now sketch how a dialogue system for theory-building persuasion dialogues can be defined. My aim is not to give a precise definition but to outline some principles that can be applied in defining such systems, with special attention to how they promote relevance and coherence in dialogues. A full formal implementation of these principles will require non-trivial work (in Section 5 two systems which implement these principles will be briefly discussed).

Throughout this section I shall use Bayesian probabilistic networks (BNs) as a running example. Very briefly, BNs are acyclic directed graphs where the nodes stand for probabilistic variables which can have one of a set of values (for example, true or false if the variable is Boolean, like in ‘The suspect killed the victim’) and the links capture probabilistic dependencies, quantified as numerical conditional probabilities. In addition, prior probabilities are assigned to the node values (assigning probability 1 to the node values that represent the available evidence). The posterior probability concerning certain nodes of interest given a body of evidence can then be calculated according to the laws of probability theory, including Bayes’ theorem. Below I assume that the dialogue is about whether a given node (the dialogue topic) in the BN has a posterior probability above a given proof standard. For example, for the statement that the suspect killed the victim it could be a very high probability, capturing ‘beyond reasonable doubt’.

The first principle then is that the communication language and protocol are defined such that each move operates on the theory underlying the dialogue. A move can operate on a theory in two ways: either it extends the theory with new elements (in a BN this can be a variable, a link, a prior probability or a conditional probability) or it expresses a propositional attitude towards an element of the theory (in a BN this can consist of challenging, conceding or retracting a link, a prior probability or a conditional probability). This is the first way in which a system for theory-building dialogues can promote relevance, since each utterance must somehow pertain to the theory built during the dialogue.

The second principle is that at each stage of a dialogue the theory constructed thus far gives rise to some current outcome, where the possible outcome values are at least partially ordered (this is always the case if the values are numeric). For example, in a BN the current outcome can be the posterior probability of the dialogue topic at a given dialogue stage. Or if the constructed theory is an argumentation framework in the sense of Dung (1995), then the outcome could be that the initial claim of the proponent is justified, defensible or overruled (where justified is better than defensible, which is better than overruled). Once the notion of a current outcome is defined, it can be used to define the current winner of the dialogue. For example, in a BN proponent can be defined the current winner if the posterior probability of the dialogue topic exceeds its proof standard while the opponent is the current winner otherwise. Or in an argumentation logic the proponent can be defined the current winner if his main claim is justified on the basis of the current theory, while the opponent is the winner otherwise. These notions can be implemented in more or less refined ways. One refinement is that the current outcome and winner are defined relative to only the ‘defended’ part of the current theory. An element of a theory is undefended if it is challenged and no further support for the element is given (however the notion of support is defined). In Prakken (2005) this idea was applied to theories in the form of argumentation frameworks: arguments with challenged premises for which no further support is given are not part of the ‘current’ argumentation framework. Likewise in a BN with, for example, a link between two nodes that is challenged.

The notions of a current outcome and current winner can be exploited in a dialogue system in two ways. Firstly, the ordering on the possible values of the outcome can be used to characterize the quality of each participant’s current position, and then the protocol can require that each move (or each attacking move) must improve the speaker’s position. For dialogues over BNs this means that each (attacking) utterance of the proponent must increase the posterior probability of the dialogue topic while each (attacking) utterance of the opponent must decrease it. This is the second way in which a protocol for theory-building dialogues can promote relevance. The notions of current outcome and winner can also be used in a turntaking rule: this rule could be defined such that the turn shifts to the other side as soon as the speaker has succeeded in becoming the current winner. In our BN example this means that the turn shifts to the opponent (proponent) as soon as the posterior probability of the dialogue topic is above (below) its proof standard. This rule was initially proposed by Loui (1998) for dialogues over argumentation frameworks, in combination with the protocol rule that each utterance must improve the speaker’s position. His rationale for the turntaking rule was that thus effectiveness is promoted since no resources are wasted while fairness is promoted since as soon as a participant is losing, she is given the opportunity to improve her position. The same rule is used in Prakken (2005). This is the third way in which a dialogue system for theory-building dialogues can promote relevance.

5. Two example systems
In this section I summarise two recent systems of the theory-building kind that I developed in collaboration with others: Joseph & Prakken’s (2009) system for discussing norm proposals in terms of a coherence network, more fully described in Joseph (2010), and Bex & Prakken’s (2008) system for discussing crime scenarios formed by causal-abductive inference, more fully described in Bex (2009).

5.1. Discussing norm proposals in terms of coherence
Paul Thagard (e.g. 2002) has proposed a coherence approach to modelling cognitive activities. The basic structure is a ‘coherence graph’, where the nodes are propositions and the edges are undirected positive or negative links (‘constraints’) between propositions. For example, propositions that imply each other positively cohere while propositions that contradict each other negatively cohere. And a proposal for an action that achieves a goal positively coheres with that goal while alternative action proposals that achieve the same goal negatively cohere with each other. Both nodes and edges can have numerical values. The basic reasoning task is to partition the nodes of a coherence graph into an accepted and a rejected set. Such partitions can be more or less coherent, depending on the extent to which they respect the constraints. In a constraint satisfaction approach a partition’s coherence can be optimized by maximising the number of positive constraints satisfied and minimising the number of constraints violated. This can be refined by using values of constraints and nodes as weights.

Building on this, Joseph (2010) proposes to model intelligent agents as coherence-maximising entities, combining a coherence approach with a Belief-Desire-Intention architecture of agents. Among other things, Joseph models how agents can reason about the norms that should hold in the society of which they are part, given the social goals that they want to promote. She then defines a dialogue system for discussions on how to regulate a society (extending the preliminary version of Joseph & Prakken 2009). The system is for theory-building dialogues in which the theory built is a coherence graph. The agents can propose goals or norms and discuss related matters of belief. The notions of current outcome and winner are defined in terms of the agents’ preferred partitions of the coherence graph, which for each agent are the partitions with an accepted set that best satisfies that agent’s norm proposals and best promotes its social goals: the more norms satisfied and the more goals promoted, the better the partition is.

5.2 Discussing crime scenarios in terms of causal-abductive inference
Building on a preliminary system of Bex & Prakken (2008), Bex (2009) proposes a dialogue system for dialogues in which crime analysts aim to determine the best explanation for a body of evidence gathered in a crime investigation. Despite this cooperative attitude of the dialogue participants, the dialogue setting is still adversarial, to prevent the well-known problem of ‘tunnel vision’ or confirmation bias, by forcing the participants to look at all sides of a case.

The participants jointly construct a theory consisting of a set of observations plus one or more explanations of these observations in terms of causal scenarios or stories. This joint theory is evaluated in terms of a logical model of causal-abductive inference (see e.g. Console et al. 1991). In causal-abductive inference the reasoning task is to explain a set of observations O with a hypothesis H and a causal scenario C such that H combined with C logically implies O and is consistent. Clearly, in general more than one explanation for a given set of observations is possible. For example, a death can be caused by murder, suicide, accident or natural causes. If alternative explanations can be given, then if further investigation is still possible, they can be tested by predicting further observations, that is, observable states of affairs F that are not in O and that are logically implied by H + C. For example, if the death was caused by murder, then there must be a murder weapon. If in further investigation such a prediction is observed to be true, this supports the explanation, while if it is observed to be false, this contradicts the explanation. Whether further investigation is possible or not, alternative explanations can be compared on their quality in terms of two criteria: the degree to which they conform to the observations (evidence) and the plausibility of their causal scenarios.

Let me illustrate this with the following dialogue, loosely based on a case study of Bex (2009), on what caused the death of Lou, a supposed victim of a murder crime.
P1: Lou’s death can be explained by his fractured skull and his brain damage, which were both observed. Moreover, Lou’s brain damage can be explained by the hypothesis that he fell.
O2: But both Lou’s brain damage and his fractured skull can also be explained by the hypothesis that he was hit on the head by an angular object.
P3: If that is true, then an angular object with Lou’s DNA on it must have been found, but it was not found.

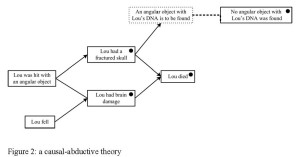
In P1 a first explanation is constructed for how Lou died, and in O2 an alternative explanation is given. The latter is clearly better since it explains all observations, while the first fails to explain Lou’s fractured skull. Then P3 attacks the latter explanation by saying that one if its predictions is contradicted by other evidence. The resulting causal-abductive theory is displayed in Figure 2, in which boxes with a dot inside are the observations to be explained, solid boxes without dots are elements of hypotheses, the dotted box is a predicted observation, solid arrows between the boxes are causal relations and the dotted link expresses contradiction.  This theory contains two alternative explanations for Lou’s death, namely, the hypotheses that Lou fell and that he was hit with an angular object, both combined with the causal relations needed to derive the observations (strictly speaking the combination of the two explanations also is an explanation but usually only minimal explanations are considered).

But this is not all. In Section 4 I said that, by way of refinement, parts of a theory built during a dialogue may be challenged and must then be supported, otherwise they should be ignored when calculating the current outcome and current winner. In fact, Bex here allows that support for elements of a causal-abductive theory is given by arguments in the sense of an argumentation logic. Moreover, he defines how such arguments can be constructed by applying argument schemes, such as those for witness or expert testimony, and how they can be attacked on the basis of critical questions of such schemes. So in fact, the theory built during a dialogue is not just a causal-abductive theory but a combination of such a theory with a logical argumentation framework in the sense of Dung (1995).

Consider by way of illustration the following continuation of the above dialogue. (Here I slightly go beyond the system as defined in Bex (2009), which does not allow for challenging elements of a causal-abductive theory with a ‘why’ move but only for directly moving arguments that support or contradict such elements.)
O4: But how do you know that no angular object with Lou’s DNA on it was found?
P5: This is stated in the police rapport by police officer A.
P6: By the way, how do we know that Lou had brain damage?
O7: This is stated in the pathologist’s report and he is an expert on brain damage.
P8: How can being hit with an angular object cause brain damage?
O9: The pathologist says that it can cause brain damage, and he is an expert on brain damage.
O10: By the way, how can a fall cause brain damage?

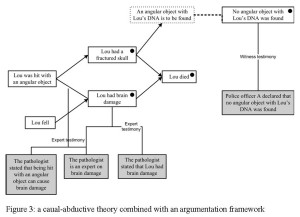
First O4 asks for the ground of P’s statement that no angular object with Lou’s DNA on it was found, which P5 answers by an application of the witness testimony scheme. Then P6 asks where the observation that Lou had brain damage comes from, which O7 answers with an argument from expert testimony. Then P8 challenges a causal relation in O’s explanation, which O9 then supports with another argument from expert testimony. In his turn O10 challenges a causal relation in P’s explanation, which P fails to support. The resulting combination of a causal-abductive theory with an ‘evidential’ argumentation framework is displayed in Figure 3 (here shaded boxes indicate that the proposition is a premise of an argument, and links without arrows are inferences, in this case applications of argument schemes).

To implement the notions of a current outcome and current winner, Bex (2009) first defines the quality of causal explanations in terms of two measures: the extent to which they explain, are supported or are contradicted by the evidence, and the extent to which the causal relations used in the explanation are plausible. Roughly, the plausibility of a causal relation is reduced by giving an argument against it, and it is increased by either defeating this argument with a counterargument or directly supporting the causal relation with an argument. (Bex also defines how the plausibility of an explanation increases if it fits a so-called story scheme, but this will be ignored here for simplicity.) Then the current outcome and winner are defined in terms of the relative quality of the explanations constructed by the two participants. It is thus clear, for instance, that P3 improves P’s position since it makes O’s explanation being contradicted by a new observation. Likewise, O4 improves O’s position since it challenges this new observation, which is therefore removed from the currently defended part of the causal-abductive theory and so does not count in determining the current quality of O’s explanation, which therefore increases. In the same way, P8 improves P’s position by challenging a causal relation in O’s explanation, after which O9 improves O’s position by supporting the challenged causal relation with an argument (note that in this example the criterion for determining the current winner, that is, the proof standard, is left implicit).

A final important point is that the arguments added in Figure 3 could be counterattacked, for instance, on the basis of the critical questions of the argument schemes from witness and expert testimony. The resulting counterarguments could be added to Figure 3 in the same way as in Figure 1. If justified, their effect would be that the statements supported by the attacked arguments are removed from the set O of observations or from the set C of causal relations. In other words, these would not be in the defended part of the causal-abductive theory and would thus not count for determining the current outcome and winner. For example, if O succeeds in discrediting police officer A as a reliable source of evidence, then the quality of O’s position is improved since its explanation is no longer contradicted by the available evidence.

6. Conclusion
This paper has addressed the relation between formal-logical and formal-dialogical accounts of argumentation. I have argued how persuasive argumentation as a kind of dialogue is possible without assuming arguments (and counterarguments) as inferential structures. The motivation for this paper was that the object of a conflict of opinion (which persuasion dialogues are meant to resolve) cannot always be most naturally cast in the form of arguments but sometimes conforms to another kind of inference, such as abduction, statistical reasoning or coherence-based reasoning. I have accordingly proposed the notion of a theory-building argumentation dialogue, in which the participants jointly build a theory that is governed by some notion of inference, whether argument-based or otherwise, and which can be used to characterize the object of their conflict of opinion. I then proposed some principles for designing systems that regulate such dialogues, with special attention for how these principles promote relevance and coherence of dialogues. Finally, I discussed two recent dialogue systems in which these ideas have been applied, one for dialogues over connectionist coherence graphs and one for dialogues over theories of causal-abductive inference. The discussion of the latter system gave rise to the observation that sometimes theories that are not argument-based must still be combined with logical argumentation frameworks, in order to model disagreements about the input elements of the theories.

REFERENCES
Bex, F.J. (2011), Arguments, Stories and Criminal Evidence. A Formal Hybrid Theory. Dordrecht: Springer Law and Philosophy Library, no 92.
Bex. F.J., & Prakken, H. (2008). Investigating stories in a formal dialogue game. In T.J.M. Bench-Capon & P.E. Dunne (Eds.): Computational Models of Argument. Proceedings of COMMA 2008 (pp. 73–84). Amsterdam: IOS Press.
Console, L., Dupré, D.T., & Torasso, P. (1991). On the relationship between abduction and deduction. Journal of Logic and Computation, 1, 661–190.
Dung, P.M. (1995). On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n–person games. Artificial Intelligence, 77, 321–357.
Gordon, T.F. (1995). The Pleadings Game. An Artificial Intelligence Model of Procedural Justice. Dordrecht/Boston/London: Kluwer Academic Publishers.
Hamblin, C.L. (1970). Fallacies. London: Methuen.
Hamblin, C.L. (1971). Mathematical models of dialogue. Theoria, 37, 130–155.
Joseph, S. (2010). Coherence-Based Computational Agency. Doctoral dissertation Universitat Autònoma de Barcelona, Spain.
Joseph S., & Prakken, H. (2009). Coherence-driven argumentation to norm consensus. Proceedings of the Twelfth International Conference on Artificial Intelligence and Law (pp. 58–67). New York: ACM Press.
Lodder, A.R. (1999). DiaLaw. On Legal Justification and Dialogical Models of Argumentation. Dordrecht: Kluwer Law and Philosophy Library, no. 42.
Loui, R.P. (1998). Process and policy: Resource–bounded nondemonstrative reasoning. Computational Intelligence, 14, 1–38.
Mackenzie, J.D. (1979). Question-begging in non-cumulative systems. Journal of Philosophical Logic, 8, 117–133.
Modgil, S., & Caminada, M. (2009). Proof theories and algorithms for abstract argumentation frameworks. In Rahwan & Simari (2009) (pp. 105–129).
Parsons, S., Wooldridge, M., & Amgoud, L. (2003). Properties and complexity of some formal inter-agent dialogues. Journal of Logic and Computation, 13, 347–376.
Prakken, H. (2005). Coherence and flexibility in dialogue games for argumentation, Journal of Logic and Computation, 15, 1009–1040.
Prakken, H. (2006). Formal systems for persuasion dialogue. The Knowledge Engineering Review, 21, 163–188. Revised and condensed version in Rahwan & Simari (2009) (pp. 281–300).
Prakken, H. (2008). A formal model of adjudication dialogues. Artificial Intelligence and Law, 16, 305–328.
Prakken, H. (2010). On the nature of argument schemes. In C.A. Reed & C. Tindale (Eds.) Dialectics, Dialogue and Argumentation. An Examination of Douglas Walton’s Theories of Reasoning and Argument (pp. 167–185). London: College Publications.
Prakken, H., & Sartor, G. (1997). Argument–based extended logic programming with defeasible priorities. Journal of Applied Non–classical Logics, 7, 25–75
Rahwan, I., & Simari, G.R. (Eds.) (2009). Argumentation in Artificial Intelligence. Berlin: Springer.
Thagard, P. (2002). Coherence in Thought and Action. Cambridge, MA: MIT Press.
Walton, D.N. (1996). Argumentation Schemes for Presumptive Reasoning. Lawrence Erlbaum Associates, Mahwah, NJ.
Walton, D.N., & Krabbe, E.C.W. (1995). Commitment in Dialogue. Basic Concepts of Interpersonal Reasoning. State University of New York Press, Albany (New York).
Woods, J., & Walton, D.N. (1978). Arresting circles in formal dialogues. Journal of Philosophical Logic, 7, 73–90.