ISSA Proceedings 2010 – Hidden Premises, Hidden Treasures?

1. Introduction
Suppose one is confronted with the following argument:
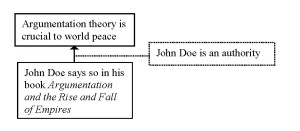
(1) Argumentation theory is crucial to world peace. John Doe says so in his book Argumentation and the Rise and Fall of Empires.

How would one go about criticizing this argument? The most obvious reaction seems to be ‘who is John Doe?’ Or maybe: ‘John Doe is just saying so because he wants his research funded.’ Another criticism could be ‘Frans van Eemeren says exactly the opposite’. Or ‘John Doe also says that the moon is made of green cheese!’.
If we take look at the original argument, it is not right away clear what this criticism is directed at. It does not challenge the premise – the antagonist is not wondering whether in his book John Doe indeed did say that argumentation theory is crucial to world peace. Yet it is an effective way to argue against the argument.

It is (almost) generally accepted among argumentation theorists that critical reactions like these are directed at the hidden premise of the argument: a premise that is unexpressed but nevertheless forms part of the argumentation put forward. Moreover, most scholars agree that this premise is different from what Van Eemeren and Grootendorst have named the ´logical minimum´ a conditional sentence of which the antecedent contains the premise (or premises, in the case of coordinative argumentation) and the consequent the claim under discussion.

In this paper I will argue that the logical minimum is an adequate representation of the unexpressed premise. Not only are the grounds to reject it questionable, there are advantages to incorporating the logical minimum in the argumentation structure. A distinction between the hidden premise and its ground makes the consequences of criticizing the hidden premise less severe. Apart from that, it makes it possible to list critical questions connected to an argumentation scheme in a more systematic way. Of course including the logical minimum brings about difficulties, and I will discuss two. First of all, it will be very difficult to formulate the ‘underlying principles’ in a systematic way. Secondly, the analyst may run the risk of making all reasoning deductively valid – even clearly invalid reasoning. But there is a bonus to this approach as well: expressing an unexpressed premise in the way I propose may help in bridging the gap between argumentation theory and logic.

2. Rejection of the logical minimum
The most straightforward way to make the hidden premise explicit is to formulate a conditional with the antecedent containing the premise and the consequent containing the conclusion. To use an example by Van Eemeren and Grootendorst (1992, p. 64):
(2) Angie is nosy, since she is a real woman.

The hidden premise in this example can be formulated as ‘If Angie is a real woman, then Angie is nosy.’ Van Eemeren and Grootendorst have named this premise the logical minimum.

Although everyone would acknowledge that this conditional represents the assumption that the claim under discussion follows from the premise put forward in support of this claim, the logical minimum is not seen as an adequate representation of the unexpressed premise. Hitchcock for instance claims that the unexpressed premise (or – to use his terminology – the ‘argument’s assumption’) is a specific universal generalisation of the if-then sentence containing the premise in the antecedent and the conclusion in the consequent (1985, p. 89).Van Eemeren and Grootendorst also reject the logical minimum and want it to be replaced by the pragmatic optimum ‘Real women are nosy’, for the following reason:
‘Pragmatically, this [adding the logical minimum–jmg] is not enough. From the very fact that he advances this particular argumentation for his standpoint it is already clear that the speaker assumes that this conclusion follows from this premise. The logical minimum contributes nothing new, and is, therefore, superfluous. Identifying this logical minimum as the unexpressed premise means that a violation of the third rule of communication [be efficient – jmg] is unnecessarily ascribed to the speaker’ (Van Eemeren & Grootendorst 1992, p. 64).

In my opinion, there is no reason not to equate the unexpressed premise with the logical minimum. To be sure, the logical minimum is ‘implied’ by explicitly putting forward the direct premise and drawing the conclusion from it: in order to make the reasoning logically valid the logical minimum has to be added. That is why the speaker can leave the unexpressed premise (or the direct premise, or the standpoint) implicit (perhaps in order to avoid a violation of the third rule of communication). It is peculiar to claim that the analyst attributes such a violation to the speaker when making the unexpressed premise explicit.

More importantly however, Van Eemeren and Grootendorst concede that ‘there are contexts where the analyst is forced to consider the logical minimum to be the pragmatic optimum’ (Van Eemeren en Grootendorst 1992, p. 66). This can for instance be the case when a point of view is supported by an elaborate coordinatively compound argumentation. If the pragma-dialectical analysis is correct, then the speaker in such contexts would necessarily be guilty of a violation of the Cooperative Principle, which would be odd, given that the argumentation in such cases can be perfectly acceptable.

Finally, the analysis Van Eemeren and Grootendorst provide is problematic when the speaker does not leave the connecting premise implicit, but the standpoint, as in (3):
(3) If it is¨pouring – as it is now –, there is no reason to water the plants.

If we reason along the same lines, completing the reasoning by adding the standpoint ‘therefore, there is no reason to water the plants’ would lead to a violation of the third rule of communication. After all, the standpoint left unexpressed would be implied by putting forward the direct premise in combination with the connecting premise. It is hard to see how the logical minimum could be replaced by a pragmatic optimum in such a case.

The reasons to reject the logical minimum as an adequate representation of the unexpressed premise are not only questionable, there is also a disadvantage to replacing the logical minimum by the pragmatic optimum. Let us take another look at the argumentation put forward in (1). The argumentation structure – including the pragmatic optimum – can be represented as follows (Scheme 1):

Now let us take a look at the criticism put forward in response to the argumentation:
(4a) Who is John Doe?
(4b) John Doe is just saying so because he wants his research funded.
(4c) Frans van Eemeren says exactly the opposite.
(4d) John Doe also says that the moon is made of green cheese!

It is clear what (4a) and (4d) are aimed at: both amount to questioning the authority of John Doe and can therefore be seen as criticizing the pragmatic optimum. However, it is not clear what part of the argumentation structure is criticized by (4b) and (4c). In those two statements, the authority of John Doe is not challenged, nor is it disputed that John Doe claimed that argumentation is crucial to world peace. Yet both (4b) and (4c) are relevant responses to the argumentation put forward.

3. Advantages to including the logical minimum in the argumentation structure
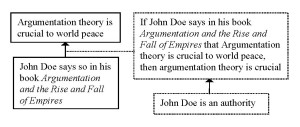
The disadvantage to replacing the logical minimum by the pragmatic optimum mentioned above, can be avoided if the logical minimum is included in the reconstruction of the argumentation structure. This does not mean that the pragmatic optimum plays no role in the argumentation. I would suggest that it can be seen as the ground for maintaining the logical minimum, resulting in the following argumentation structure (Scheme 2):

In this structure (Scheme 2), it is clear where (4b) and (4c) are aimed at. They both challenge the connection between John Doe being an authority and accepting what John Doe says as true. In a sense, they both question whether it is true that ‘If John Doe is an authority, then what he says about argumentation theory being crucial to world peace is true’. (4b) questions whether we should accept John Doe’s opinions because he has vested interests, (4c) points at another authority who has a different opinion on the matter.

I would claim that it is important to make a distinction between the logical minimum and the grounds one has for maintaining this logical minimum. In this analysis, the logical minimum is a premise like all others. This means that the evaluation of such premises can proceed along the line in which other premises are evaluated: if a logical minimum is challenged, the speaker will have to support it, or retract it. The ground put forward in support of the logical minimum can subsequently be criticized by showing that the ground is untrue, or by showing that the ground does not justify the conclusion that the logical minimum is true.

This last way of criticizing is of special interest, since it brings an advantage: one could accept the ground and still reject the logical minimum. In such cases, one can accept the general rule, but deny that – or question whether – this general rule is applicable in a specific case. If we take the following dialogue:
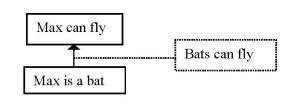
(5) Tony: Max can fly.
Bob: How do you know?
Tony: Bats can fly
Bob: Max can’t fly, his wings are torn.

Analysed in the traditional way, the argumentation structure which is reflected in this dialogue would be (Scheme 3):

The criticism put forward by Bob can be seen as directed only at the pragmatic optimum ‘Bats can fly’. The direct premise is accepted, whereas the conclusion is rejected. Therefore, the second premise must be rejected and ‘Bats can fly’ must be retracted.

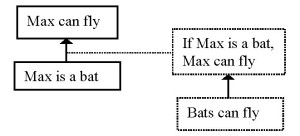
When the pragmatic optimum is seen as the ground for the truth of the logical minimum, the consequences of Bob’s criticism are less serious. In this analysis, the argumentation has the following structure (Scheme 4):

 

 

 

 

 

 

Bob accepts that Max is a bat. He does not want to commit himself to the logical minimum ‘If Max is a bat, he can fly’. The torn wings confirm that the antecedent of this conditional is true whereas the consequent is false, and therefore the conditional is false. In this analysis, it does not mean that he has to reject the general statement ‘bats can fly’. He can maintain this statement, whilst denying that from this general statement the particular statement ‘If Max is a bat, Max can fly’ can be deduced. The criticism is directed not at the general statement that forms the ground of the unexpressed premise, but at the connection between this general statement and the specific conditional statement that functions as a connecting premise.

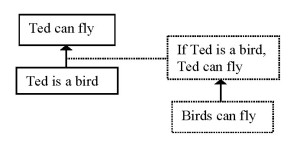
One could even think of an example where both the pragmatic optimum and the connection between the pragmatic optimum and the logical minimum are challenged, as in (6):
(6) Jill: Ted can fly.
Peter: How do you know?
Jill: Birds can fly.
Peter: Ted can’t fly, his wings are torn. And besides, he is a penguin.

In (6), Peter challenges the connection between the pragmatic optimum and the logical minimum by pointing out that Ted’s wings are torn and questions the truth of the pragmatic optimum by making clear there is a category of birds that cannot fly (Scheme 5).

There is a second advantage – of a more practical nature – to including the logical minimum in the argumentation structure: it makes it possible to list critical questions to an argumentation scheme in a more systematic way.

Over the years, argumentation theorists have described a great amount of argumentation schemes. Walton, Reed and Macagno provide an user’s compendium of schemes that comprises 60 different ones, with many having over five subtypes, resulting in about one hunderd varieties (2008, pp. 308-346). The amount of critical questions associated to these schemes differs considerably. An argument from waste can be criticized by two, whereas value-based practical reasoning can be criticized by seven critical questions. Moreover, the critical questions described in the literature (that has been very conveniently summarized by Walton, Reed and Magnano) are not all of the same nature. Let me try to explain what I mean by this by comparing two argumentation schemes that Walton, Reed and Macagno discuss: argument from expert opinion and argument from witness testimony.

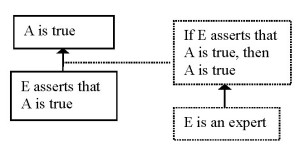
An argument from expert opinion can be described as having the following structure (the wording of the premises and the conclusion is by Walton, Reed and Macagno, the schematic representation I have altered so to make it easier to compare this argumentation scheme with the argument from authority discussed earlier)(Scheme 6):

For this argumentation scheme, the following critical questions have been proposed (Walton, Reed and Macagno 2008, p. 310):
(7a) How credible is E as an expert source?
(7b) Is E an expert in the field?
(7c) What did E assert that implies A?
(7d) Is E personally reliable as a source?
(7e) Is A consistent with what other experts assert?
(7f) Is E’s assertion based on evidence?

Of these questions, (7a) and (7b) seem to question the ground for the logical minimum; they question whether E is an expert indeed. (7c) seems not to criticize the argumentation scheme, but the direct premise: is it true that E asserts that A is true? (7d) and (7e) seem to criticize the connection between the ground and the logical minimum. From the outset, it is not quite clear what (7f) is aimed at – it seems to be an independent support of the claim that A is true.

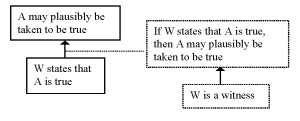
If we compare this list of critical questions to the one provided for witness testimony, we find some striking differences. An argument from witness testimony can be schematically represented as follows (again, wording by Walton et al., adjusted schematic representation)(Scheme 7):

The critical questions that accompany this argumentation scheme are:
(8a) Is what the witness said internally consistent?
(8b) Is what the witness said consistent with other known facts of the case?
(8c) Is what the witness said consistent with testimonies of other witnesses?
(8d) Is there some kind of bias that can be attributed to his account?
(8e) How plausible is the statement A asserted by the witness?

First of all, it is striking that none of these questions is directed at the ground in support of the logical minimum, although it seems reasonable enough to question whether someone really was a witness – really was in a position to see what happened. A second difference between this list and the list of critical questions related to the scheme of expert opinion is that there is no critical question that challenges the direct premise: it is not challenged that W indeed said that A. The majority of the questions is aimed at the connection between the ground and the logical minimum. (8a) to (8d) all presuppose that W is a witness, and question whether this means that what W says may plausibly be taken to be true. The final question seems (like (7f) in the case of expert opinion) directed at the claim under discussion.

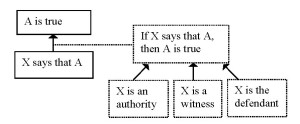
These differences are all the more remarkable since both argumentation schemes seem to hinge on the same principle: in both cases a statement is taken to be true / plausible because someone (an expert or a witness) has said that it is true. In that sense, they can be seen as two of the same kind: having a similar logical minimum, but a different ground in support of it (Scheme 8).

In sum, including the logical minimum provides a heuristic benefit as well: in listing the critical questions, one can check whether indeed all parts of the argumentation structure have been scrutinized. Moreover, if all elements of the argumentation structure are made explicit in such a way, the correspondence between different schemes becomes apparent.

4. Difficulties in adding the logical minimum to the argumentation structure
Although I hope I have been able to indicate some benefits to including the logical minimum in the reconstruction of the argumentation structure, I do realize that the proposed approach brings along difficulties as well. The first difficulty is closely related to the general argumentation structure just sketched. By including the logical minimum and thereby differentiating between the connecting premise and its ground, the question rises how this connection should be formulated. If the logical minimum is included, a second arrow is introduced connecting the logical minimum to its ground. Now what is it this arrow stands for? Should one modestly state that the arrow reads ‘If X is an authority then if X says A, A is true’, or is a more general principle – like ‘What an authority says is true’ – in place? It will be difficult (but challenging) to find a formulation that characterizes the argumentation used and is not too general (since in that case it will be too easy to attack it).

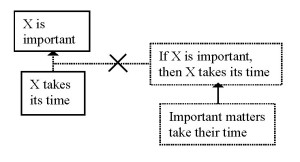
A second difficulty is that in reconstructing the argumentation structure in the way I proposed, the analyst runs the risk of turning invalid reasoning into valid reasoning. An example may clarify what I mean. Suppose the analyst is confronted with the following line of reasoning (taken from Van Eemeren and Grootendorst 1996, p. 94):
(9) son: ‘Mr. Townsend called.’
father: ‘Anything important?’
son: ‘he said he would call again next year.’
father: ‘then it is important. Important matters take their time.’

In reconstructing the reasoning put forward by the father, the unattentive analyst might discern the claim ‘It is important’, the premise ‘Important matters take their time’ and add the conditional sentence ‘If important matters take their time, then this is important’ so as to turn the reasoning into a modus ponendo ponens. Of course the analyst thereby overlooks the fact that the father commits the fallacy of affirming the consequent. The general statement ‘Important matters take their time’ must not be seen as the direct premise, but as the ground for the logical minimum, as in the following schematic representation (Scheme 9):

It is clear right away that this logical minimum is not the same as a conditional where the premise is expressed in the antecedent and the claim in the consequent, and hence the reasoning does not represent an instance of modus ponendo ponens.

This means that in reconstructing the argumentation structure according to this proposal, the analyst needs to be able to differentiate between statements that function as a direct premise and statements that form the ground for the logical minimum; an excercise that can be a tricky one.

5. Summary and conclusions
Despite the difficulties mentioned in the last section, I hope that the proposal not to discard the logical minimum but to include it in the reconstruction of the argumentation structure is an interesting one. I have tried to show that the reasons to replace the logical minimum by the pragmatic optimum are not convincing and that including the logical minimum does have advantages. Not only does it mitigate the consequences of an attack at the hidden premise, by allowing the opportunity of retaining the ground of the hidden premise whilst rejecting the logical minimum. There is also a heuristic benefit to the reconstruction proposed. Incorporating the logical minimum brings correspondences between different argumentation schemes to the surface, since these schemes can be regarded as having a similar logical minimum but different grounds for maintaining it. Moreover, by making the various elements of the argumentation structure explicit, in listing the critical questions one can make sure that indeed all those elements have been adequately scrutinized.

Finally, there is a bonus to acknowledging the role of the logical minimum, since it may help to clarify an issue that has been discussed exhaustively among logicians. Although generally argumentation theorists are not that keen on logical paradoxes, maybe this case will raise your interest, since it is argumentation theory that may provide a way out. The logical paradox I am referring to is the following (Cooper 1978, p. 183):
(10) If Brown wins the election, Smith will retire to private life.
If Smith dies before the election, Brown will win the election.
So: If Smith dies before the election, Smith will retire to private life.

The reasoning in (10) can symbolically be represented as follows (Scheme 10):

 

The argument form represented in (10’) is deductively valid: if the premises are true, the conclusion is necessarily true as well. Yet the natural language instance in (10) clearly yields a conclusion that is untenable.

How can argumentation theory, and especially the notion of a logical minimum shed light on this logical paradox? As is mentioned above, the logical minimum is a conditional sentence where the antecedent contains the premise and the consequent the claim under discussion. This means that the symbolic representation of for example modus ponendo ponens reads as follows (Scheme 11):

This interpretation of the symbolic representation of the conditional connective puts a restraint on the propositions that can be filled in for p and q: it must be possible to assert those propositions independently. In Frege’s words: both p and q must contain a Gedanke (1964: 2), something that can be judged to be true or false (1993: 84-85). After all, the same propositions form the premise and the claim put forward (Gerlofs 2009: 97).

If we take a look at the conditional sentences in (10) with this in mind, it becomes clear why this instance of an hypothetical syllogism is an incorrect one. Neither of the conditionals expressed in (10) could function as the logical minimum, since the antecedent of the conditionals does not contain a Gedanke in Frege’s sense of the word. ‘Smith dies before the election’ is not a sentence that can be judged true or false, and hence cannot be put forward as a premise in support of a claim. The same goes for ‘Brown wins the election’. The logical minimum therefore clarifies that (10) is not a real counterexample to the deductively valid argument form of hypothetical syllogism. A reason all the more to not to discard the logical minimum too hastily.

REFERENCES
Cooper, W.S. (1978). Foundations of logica-linguistics. A unified theory of information, language and logic. Dordrecht/Boston: D. Reidel Publishing Company.
Eemeren, F.H. van, & Grootendorst, R. (1992). Argumentation, communication and fallacies. A pragma-dialectical perspective. Hilsdale NJ : Lawrence Erlbaum Associates, Publishers.
Eemeren, F.H. van, & Grootendorst, R. (1996). Leren argumenteren met Vader en Zoon. Amsterdam: Uitgeverij Contact.
Frege, G. (1964). Begriffschrift und andere Aufsätze. Hildesheim: Georg Olms Verlag.
Frege, G. (1993). ‘Gedankengefüge’. Logische Untersuchungen. 4., durchgesehene und bibliographisch ergänzte Auflage. Göttingen: Vandenhoeck und Ruprecht.
Gerlofs, J.M. (2009). The use of conditionals in argumentation. A proposal for the analysis and evaluation of argumentatively used conditionals. Dissertation. University of Amsterdam.
Hitchcock, D. (1985). Enthymematic arguments. Informal logic, VII.2&3, 83-97.
Walton, D.N., Reed, C., & Macagno, F. (2008). Argumentation schemes. Cambridge: Cambridge University Press.