ISSA Proceedings 2014 ~ A Formal Model Of Conductive Reasoning

Abstract: I propose a formal model of representation and numerical evaluation of conductive arguments. Such arguments consist not only of pro-premises supporting a claim, but also of contra-premises denying this claim. Offering a simple and intuitive alternative to accounts developed in the area of computational models of argument, the proposed model recognizes internal structure of arguments, allows infinitely many degrees of acceptability, reflects the cumulative nature of convergent reasoning, and enables to interpret attack relation.

Keywords: argument evaluation, argument structure, attack relation, conductive reasoning, logical force of argument, rebuttal.

1. Introduction
According to Wellman’s original definition (1971) the conclusion of any conductive argument is drawn inconclusively from its premises. Moreover, the premises and the conclusion are about one and the same individual case, i.e. the conclusion is drawn without appeal to any other case. Wellman also gave three leading examples of conductive arguments, which determine three patterns of conduction:

(1) You ought to help him for he has been very kind to you.
(2) You ought to take your son to the movie because you promised, and you have nothing better to do this afternoon.
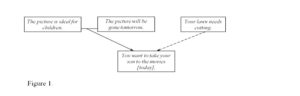
(3) Although your lawn needs cutting, you want to take your son to the movies because the picture is ideal for children and will be gone by tomorrow.

Wellman’s definition was an object of many interesting views, opinions and interpretations, mostly surveyed in (Blair & Johnson 2011). However, we do not discuss this issue here, but we simply follow these authors who, as Walton & Gordon (2013), focus on the third pattern and propose to take conductive arguments to be the same as pro-contra arguments. Such arguments, except of a normal pro-premise or premises (The picture is ideal for children; It will be gone by tomorrow), have also a con-premise or premises (Your lawn needs cutting).

In the next two chapters we analyze conductive arguments from the logical point of view. The conduction is regarded here as one act of reasoning, in which a conclusion is drawn by the same time from both types of premises. In Chapter 2 we describe the structure and in Chapter 3 – a method of evaluation of conductive arguments. This method is based on the model of argument proposed in (Selinger 2014). In Chapter 4 we introduce a dialectical component of the analysis. Namely, by means of our model, we discuss definition of attack relation holding between arguments.

2. Structure of conductive arguments
There are many ways of expressing conductive arguments in natural language. Some of them are the following:

– Since A, even though B, therefore C.
– A, therefore C, although B.
– Although B, C because A.
– B, but (on the other hand) A, therefore C.
– Despite B, (we know that) A, therefore C.

In the above schemes the letter A represents a pro-premise (or pro-premises), B – a con-premise (or con-premises) and C – a conclusion. It is worth to note that pro-premises are presented as overcoming con-premises, so that an argument can be accepted if they really do. There are two types of inference in conductive arguments: pro-premises support and con-premises deny (contradict, attack) conclusions. They can be represented using the standard diagramming method. Figure 1 shows the diagram of Wellman’s third example.

Relation of support is represented by the solid and relation of contradiction – by the dashed line.[i] In order to reflect this duality in our formal model we follow Walton & Gordon’s idea involving the assignment of Boolean values to these two types of inference, however, we propose to use simpler formal structures than the so-called argument graphs (cf. Walton & Gordon 2013).

Let L be a language, i.e. a set of sentences. Sequents are all the tuples of the form <P, c, d>, where P ⊆ L is a non-empty, finite set of sentences (premises), c ∈ L is a single sentence (conclusion), and d is a Boolean value (1 in pro-sequents and 0 in con-sequents). An argument is simply any finite, non-empty set of sequents. If an argument consists of only one sequent then it will be called an atomic argument.

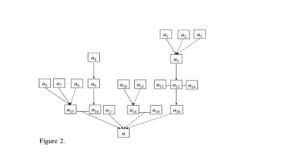
The premises of an argument are all the premises of all its sequents. The conclusions of an argument are all the conclusions of all its sequents. The first premises are those premises, which are not the conclusions, and the final conclusions are those conclusions, which are not the premises. Finally, the intermediate conclusions are those sentences, which are both the conclusions and the premises. A typical (abstract) argument structure is presented in Figure 2 by the diagram corresponding to the set: {<{α1}, α5, 1>, <{α2}, α5, 0>, <{α3}, α5, 0>, <{α4}, α9, 1>, <{α5}, α13, 1>, <{α6}, α15, 1>, <{α7}, α15, 1>, <{α8}, α15, 0>, <{α9}, α16, 1>, <{α10}, α18, 1>, <{α11}, α18, 0>, <{α12, α13, α14}, α20, 1>, <{α15, α16}, α, 1>, <{α17}, α, 1>, <{α18, α19}, α, 0>, <{α20}, α, 0>}. This argument consists of 16 different sequents (10 of them are pro- and 6 are con-sequents), so it is the sum of the same number of atomic arguments. The premises are all the sentences in the diagram except of α, which is the final conclusion; the conclusions are: α5, α9, α13, α15, α16, α18, α20, α; the first premises: α1, α2, α3, α4, α6, α7, α8, α10, α11, α12, α14, α17, α19; the intermediate conclusions: α5, α9, α13, α15, α16, α18, α20.

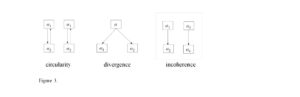
By the means of our formalism also atypical structures can be distinguished (cf. Selinger 2014). Some of them are illustrated by Figure 3. Circular arguments can have no first premises and/or no final conclusion (two examples in Figure 3 have neither the first premises nor the final conclusion). They are interesting argument structures, e.g. for those who deal with antinomies, however, we do not discuss them, since they are mostly regarded as faulty. On the other hand, divergent arguments and incoherent arguments can have more than one final conclusion. They are not faulty (unless from some purely pragmatic point of view), but they can be represented as the sums of non-divergent and coherent arguments. Therefore, when discussing evaluation of conductive arguments in the next chapter, we focus on typical argument structures like that shown in Figure 2.

3. Evaluation of conductive arguments
The central question to be considered in this section is: how to transform the values of first premises into the value of final conclusion? We answer this question in three steps concerning evaluation of atomic, convergent and, finally, conductive arguments.

First we introduce some basic notions. Each partial function v: L’→[0, 1], where L’ ⊆ L, is an evaluation function. The value v(p) is the (degree of) acceptability of p. We consider also a predefined function w: LχL→[0, 1]. The value w(c/p) is the acceptability of c under the condition that v(p) = 1, so that the function w will be called conditional acceptability.

We assume that L contains the negation connective. If the premises of some sequent deny its conclusion c then evaluation of c will be based on evaluation of the sentence ¬c in the corresponding pro-sequent, in which the same premises support ¬c. Let us note that for a perfectly rational agent the condition v(¬c) = 1 – v(c) should be satisfied. This postulate will be useful to evaluate con-sequents.

Let v be a given evaluation function (we assume that v is fixed in the following part of our exposition). By ∧P we denote the conjunction of all the sentences belonging to a finite, non-empty set P (if P is a singleton then ∧P is the sole element of P). We assume that L contains the conjunction connective, and if P⊆ dom(v) then ∧P ∈dom(v).[ii] The value w(c/∧P) will be called the internal strength of a pro-sequent <P, c, 1>, and the value w(¬c/∧P) – the internal strength of a con-sequent <P, c, 0>.

Let A = {<P, c, d>} be an atomic argument, where P ∈ dom(v), c∉ dom(v), and d is a Boolean value. The function vA is the following extension of v to the set dom(v) ∪ {c}:

(4) If d = 1 then vA(c) = v(∧P)⋅w(c/∧P);
(5) If d = 0 then vA(c) = 1 – v(∧P)⋅w(¬c/∧P).

Thus the acceptability of the conclusion of an atomic argument under condition that its premises are fully acceptable is reduced proportionally to the actual acceptability of the premises. The value vA(c) will be called the (logical) strength (or force) of an argument A. We will say that a pro-argument is acceptable iff its strength is greater than ½, and a con-argument is acceptable iff its strength is smaller than ½.

In the next step we consider evaluation of convergent reasoning. Since convergent argumentation is used to cumulate the forces of different reasons supporting (or denying) a claim we have to add these forces in a way adapted to our scale. Strengths of pro- and con-components will be added separately in each of both groups, independently of the other. Let A = A1 ∪ A2 , where both A1 and A2 are acceptable arguments and they either consist of only pro- or of only con-sequents having the same conclusion c. Let vA1(c) = a1 and vA2(c) = a2.

(6) If A1 and A2 are independent pro-arguments, and a1, a2 > ½, then vA(c) = a1 ⊕a2;
(7) If A1 and A2 are independent con-arguments, and a1, a2 < ½, then vA(c) = 1 – (1–a1)⊕ (1–a2), where x ⊕ y = 2•x + 2•y – 2•x•y ¬– 1.

In (Selinger 2014) we provide a justification of this algorithm, deriving it from the principle (satisfied also by the algorithms given in (4) and (5)) that can be called the principle of proportionality, according to which the strength of argument should vary proportionally to the values assigned to its components. We also discuss properties of the operation ⊕ (here let us only mention that it is both commutative and associative, therefore the strengths of any number of converging, independent arguments can be added in any order).

Finally, we consider conductive reasoning. In order to compute the final value of a conductive argument we will subtract the strength of its con- from the strength of its pro-components in a way adapted to our scale. Let A = Apro  Acon, where Apro consists only of pro-sequents and Acon only of con-sequents having the same conclusion c. We assume that both groups of arguments are acceptable, i.e. vApro(c) > ½ and vAcon(c) < ½.

(8) If vApro(c) < 1, and vAcon(c) > 0, then vA(c) = vApro(c) + vAcon(c) ¬– ½;

The idea of this algorithm is illustrated by Figure 4. Since we want to know how much pro-arguments outweigh con-arguments (or vice versa), we subtract the value ½¬ –vAcon(c) represented by the interval [vAcon(c), ½] in this figure from the value vApro(c) – ½ represented by the interval [½, vApro(c)]. In order to finally receive the acceptability of c we add this differential to ½. Let us note that the considered value is directly proportional to the acceptability of pro- and reversely proportional to the acceptability of con-arguments, so that the algorithm satisfies the principle of proportionality.

The algorithm given by (8) assumes that both pro- and con-arguments are, as defined by Wellman, inconclusive. However in real-life argumentation it happens, for example in mathematical practice, that initial considerations concerning some hypothesis, which are based on subjective premonitions, analogies, incomplete calculations etc., are finally overcame by a mathematical proof. Then all the objections raised originally are no longer significant, and the hypothesis becomes a theorem. Therefore, if either pro- or con-arguments are conclusive, then so the whole conductive argument is.

(9) If vApro(c) = 1, and vAcon(c) ≠ 0, then vA(c) = 1;
(10) If vApro(c) ≠ 1, and vAcon(c) = 0, then vA(c) = 0.

If both pro- and con-arguments happen to be conclusive then it is an evidence of a contradiction in underlying knowledge, and the initial evaluation function requires revision. Therefore we claim that the values of such strongly antinomian arguments cannot be found.

(11) If vApro(c) = 1, and vAcon(c) = 0, then vA(c) is not computable.

Otherwise, the strength of weakly antinomian arguments, which consist of equal inconclusive components, can be computed as ½ using the algorithm given by (8).

In order to complete this section let us add that the acceptability of the conclusions of complex, multilevel argument structures, as the one represented by Figure 3, can be calculated level by level using the algorithms (4) – (10). An analogous process concerning only pro-arguments is described in (Selinger 2014).

4. Attack relation
Our goal is to define attack relation, which holds between arguments. For the sake of simplicity we consider only attack relation restricted to the set of atomic arguments. There are three components of atomic arguments that can be an object of a possible attack: premises, inferences and conclusions. The latter is the case of conduction. If we take into account a pro- and a con-argument, which have the same conclusion, then the stronger of them attacks the weaker one (in the case of an antinomy both arguments attack each other, so that it can be called the mutual attack case).

(12) An argument A attacks (the conclusion of) an argument B iff A = {<P1, c, d>}, B = {<P2, c, 1 – d >}, and either d = 0 and 1 – vA(c) ≤ vB(c), or d = 1 and 1 – vA(c) ≤ vB(c).

The second kind of attack is the attack on a premise. Obviously, it is effective if (i) some premise of an attacked argument is shown to be not acceptable on the basis of the remaining knowledge.

(13) An argument A attacks (a premise of) an argument B iff A = {<P1, c1, 0>}, B = {<P2, c2, d>}, c1 < P2, and v’A(c1) ≤ ½, where v’ is the function obtained from v by deleting c1 from its domain, i.e. dom(v’) = dom(v) – {c1}.

However, with respect to the proposed method of evaluation, two further situations are possible: (ii) the premises of an attacked argument considered separately are acceptable, however their conjunction is not; (iii) the conjunction of the premises of an attacked argument is acceptable and the internal strength of its constituent (pro- or con-) sequent is greater than ½, but the product of these values is not. Thus, in view of the evaluation method proposed here, merely weakening a premise can cause an effective attack, and the definition (13) should be replaced by the following broader one.

(13’) An argument A attacks (a premise of) an argument B iff A = {<P1, c1, 0>}, B={<P2, c2, d>}, c1 ∉P2, v’A(c1) ≤v(c1), and either d = 1 and v’A(∧P2)∧w(c2/∧P2)∧ ½, or d = 0 and v’A(∧P2) w(~c2/∧P2) ⊆ ½, where v’ is the function obtained from v by deleting c1 from its domain.

In order to consider attack on the relationship between the premises and the conclusion of an attacked argument, let us take into account the following Pollock’s example of an undercutting defeater:

(14) The object looks red, thus it is red unless it is illuminated by a red light.

Following Toulmin’s terminology, the sentence The object is illuminated by a red light will be called rebuttal. Let us note, that rebuttals are not con-premises, since they do not entail the negation of the conclusion (the fact that the object is illuminated by a red light does not imply that the object is not red). Thus Pollock’s example cannot be diagrammed like conductive arguments. Since it is an arrow that represents the inference, which is denied by the rebuttal, rather the diagram shown by Figure 5 seems to be relevant here.

However, structures such as the one in Figure 5 have no direct representation within the formalism introduced in this paper to examine conductive reasoning. In order to fill this gap we propose to add the fourth element, namely the set of rebuttals, to the sequents considered so far. Such extended sequents will have the form <P, c, d, R>, where R is the set of (linked) rebuttals.

Since our goal is to define attack relation as holding between arguments, we propose to take an argument without rebuttals (i.e. with the empty set of rebuttals) as being attacked by the argument with the same premises and conclusion, but with a rebuttal added. For example (14) can be regarded as an attacker of the simple argument

(15) The object looks red, thus it is red.

This argument (15) has the following representation: {<{The object looks red}, The object is red, 1, ∅>}, and its attacker (14): {<{The object looks red}, The object is red, 1, {The object is illuminated by a red light}>}. In general, an argument of the form {<P, c, d,∅>} can be attacked by any argument of the form {<P, c, d, R>}. Effectiveness of this sort of attack depends on evaluation of such arguments. It is not the aim of this paper to develop an evaluation method for arguments with rebuttals systematically, however, let us note that the strength of an argument {<P, c, d, R>}, where R ≠∅, seems to be strictly connected with the strength of the corresponding argument {<P∪{~∧R}, c, d, ∅>}, which has an empty set of rebuttals. For example, the strength of (14) depends on the strength of the argument:

(16) The object looks red, and it is not illuminated by a red light, thus it is red.

If this argument is acceptable then so is its second premise (The object is not illuminated by a red light), which is the negation of the rebuttal in (14). By the same the rebuttal is not acceptable so that the attack on (15) cannot be effective. Thus (16) cannot be acceptable if (14) attacks the inference of (15). In general, if A = {<P, c, d, R>} attacks (the inference of) B = {<P, c, d,∅>}, then R≠∅ and A’ = {<P∪{~∧R}, c, d, ∅>} is not acceptable. Obviously, the converse does not hold, because not any acceptable set of sentences can be a good rebuttal. If the attack is to be effective the set R must be relevant to deny the inference in B. A test of relevance that we propose is based on an observation concerning (15) and (16). Intuitively, the inference in (16) is stronger than the inference in (15), i.e. the internal strength of the sequent in (16) is greater than the internal strength of the sequent in (15). This is because (16) assumes that a possible objection against the inference in (15) has been overcome. Thus, the condition w(c/∧P∧~∧R) > w(c/∧P)  can be proposed to determine the relevance of the rebuttal in A. Following these intuitions we recognize arguments overcoming rebuttals as hybrid arguments in the sense defined by Vorobej (1995). Such arguments contain a premise that strengthens them, but this premise does not work alone so that it cannot be taken as the premise of a separate convergent reasoning (in (16) such a premise is the sentence The object is not illuminated by a red light).

Summing up, we claim that (a) non-acceptability of the hybrid counterparts corresponding to arguments having rebuttals and (b) relevance of rebuttals are necessary for attack on inference to be effective. However, we leave open the question whether they are sufficient.

5. Conclusion
We showed how the model of representation and evaluation of arguments elaborated in (Selinger 2014) can be enriched in order to cover the case of conductive reasoning. The extended model allowed us to define in formal terms two kinds of attack relation, namely attack on conclusion and attack on premise. However, the definition of attack on inference requires further extension of the model. In order to initiate more profound studies, we outlined a possible direction of making such an extension.

Acknowledgements
I would like to thank Professor David Hitchcock for his inspiring remarks concerning my ideas, and for his helpful terminological suggestions.

NOTES
i. Let us note that Walton & Gordon (2013) interpret both pro-premises as supporting the claim independently of each other, and they draw separate arrows connecting each pro-premise with the conclusion, which represent convergent reasoning. However, it seems to be problematic whether the premise The picture will be gone tomorrow alone (i.e. without any further information about the movie) actually supports the conclusion.
ii. In order to avoid this assumption the acceptability of an independent set of sentences can be calculated as the product of the values of its elements. Thus the acceptability of a conjunction can be smaller than the acceptability of its components considered separately (cf. Selinger 2014).
References
Blair, J. A., & Johnson, R. H. (2011). Conductive argument: an overlooked type of defeasible reasoning. London: King’s College Publications.
Selinger, M. (2014). Towards formal representation and evaluation of arguments. Argumentation, 26(3), 379-393. (K. Budzynska, & M. Koszowy (Eds.), The Polish School of Argumentation, the special the issue of the journal.)
Vorobej, M. (1995). Hybrid arguments. Informal Logic, 17(2), 289-296.
Wellman, C. (1971). Challenge and response: justification in ethics. Carbondale: Southern Illinois University Press.
Walton, D., & Gordon, T. F. (2013). How to formalize informal logic. In M. Lewiński, & D. Mohammed (Eds.), Proceedings of the 10th OSSA Conference at the University of Windsor, May 2013 (pp. 1-13). Windsor: Centre for Research in Reasoning, and the University of Windsor.