ISSA Proceedings 2014 ~ Think Twice: Fallacies And Dual-Process Accounts Of Reasoning
No comments yetAbstract: This paper presents some ideas of how to conceptualize thinking errors from a cognitive point of view. First, it describes the basic ideas of dual-process theories, as they are discussed in cognitive psychology. Next, it traces the sources of thinking errors within a dual-process framework and shows how these ideas might be useful to explain the occurrence of traditional fallacies. Finally, it demonstrates how this account captures thinking errors beyond the traditional paradigm of fallacies.
Keywords: fallacies, thinking errors, dual process theories, cognitive processes
1. Introduction
The last three decades have seen a rapid growth of research on fallacies in argumentation theory, on the one hand, and on heuristics and biases in cognitive psychology, on the other hand. Although the domains of these two lines of research strongly overlap, there are only scarce attempts to integrate insights from cognitive psychology into argumentation theory and vice versa (Jackson, 1995; Mercier & Sperber, 2011; O’Keefe, 1995; Walton, 2010). This paper contributes an idea on how to theorize about traditional fallacies on the basis of dual-process accounts of cognition.
2. Dual-process accounts of cognition
The basic idea of dual process theories is that there are at least two different types of cognitive processes or cognitive systems (Evans & Stanovich, 2013; Kahneman, 2011; Stanovich, 2011). System 1 consists of cognitive processes that are fast, automatic and effortless. System 1 is driven by intuitions, associations, stereotypes, and emotions. Here are some examples: When you associate the picture of the Eiffel Tower with ‘Paris’, when you give the result of ‘1+1’, or when you are driving on an empty highway, then System 1 is at work. System 2, in contrast, consists of processes that are rather slow, controlled and effortful. System 2 is able to think critically, to follow rules, to analyse exceptions, and to make sense of abstract ideas. Some examples include: backing into a parking space, calculating the result of ‘24×37’, and finding a guy with glasses, red-and-white striped shirt, and a bobble hat in a highly detailed panorama illustration. These processes take effort and concentration.
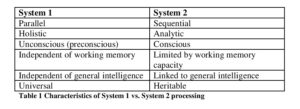
In what follows, I’m going to use processing speed as the main criterion for distinguishing between System 1 and System 2 (Kahneman, 2011). As System 1 is the fast cognitive system, its responses are always first. System 1 responses are there, long before System 2 finishes its processing. Table 1 lists some characteristics that are commonly associated with System 1 and System 2 in the literature (cf. Evans, 2008, p. 257 for further attributes associated with dual systems of thinking).
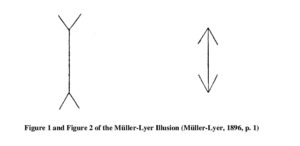
The central idea of dual-process theories is that these two cognitive systems interact with one another and that these interactions may be felicitous or infelicitous. When comparing the vertical lines in figure 1 and figure 2, one gets the impression that the shafts of the arrows differ in length. This is a response of the fast and automatic System 1. As long as one doesn’t take the effort of measuring lengths, one accepts this impression as provisionally true.
By using a ruler, one finds that–contrary to the first impression–the shafts of the arrows are of equal length. Although one knows that the shafts are of equal length, one still sees them as differing in length. One cannot switch off System 1, but one can override its impressions and tell oneself that this is an optical illusion and that one must not trust one’s sensations.
3. Felicitous interactions and sources of error
How may one apply this framework to the domain of argumentation? Consider the following argument.
Animals must be given more respect. Monkeys at the circus are dressed like pygmies in a zoo. Sheep are auctioned like on a slave market. Chickens are slaughtered like in a Nazi extermination camp.
(Adapted from the fallacyfiles.org, cf. Curtis, 2008)
System 1 might give a first response, that there is something odd about this argument, though it cannot tell straight away what exactly is wrong with it. So System 2 gets alert for checking the argument. Reflecting on the line of reasoning, System 2 may find that the argument begs the question of whether animals are morally equal to humans and that the standard view holds the reverse, i.e. humans should not be treated like animals. And therefore slave auctions, pygmy zoos, and extermination camps are morally wrong. One cannot shift the burden of proof by simply comparing animals to humans, because according to current moral standards, Pygmies, slaves and Nazi victims have more moral rights than monkeys, sheep and chickens.
This is how the interaction of System 1 and System 2 should work. System 1 produces the intuition that there is something wrong about an argument, but cannot tell what exactly it is. System 2 starts scrutinizing the argument and comes up with analytical reasons for why this is an unhappy argument.
However, the interactions of System 1 and System 2 are prone to error. There are at least four different sources of such errors (Stanovich, 2011; Stanovich, Toplak, & West, 2008). The first three errors are initiated by an incorrect response of System 1, i.e. System 1 uses a heuristic rule of thumb that works well in most every-day contexts, but not in the given context. It would be the task of System 2 to detect the error and to correct it. However, System 2 does not perform these tasks. The fourth error originates in System 2, when System 2 uses inappropriate rules or strategies for analysing a problem. The details are explained in the following paragraphs.
The first kind of error: System 2 might fail to check the intuitive response of System 1. The bat-and-ball problem is a classic example.
A bat and a ball cost $1.10. The bat costs $1.00 more than the ball.
How much does the ball cost? ____ cents
(Frederick, 2005, p. 26)
The intuitive answer is ‘10 cents’, which is wrong. If the ball costs 10 cents and the bat costs $1 more than the ball, then the bat costs $1.10. The sum of bat and ball thus equals $1.20. Many intelligent people, nonetheless, give the intuitive answer without checking for arithmetic correctness. ‘10 cents’ is the answer to an easy question, namely the question: ‘What is the difference of $1.10 and $1?’ This is a task for System 1. But that is not the original question. The original question is a hard one and cannot be answered by intuition.
It is a task for System 2
The second kind of error: System 2 might detect an error in the response of System 1, but fail to override this response.
A small bowl contains 10 jelly beans, 1 of which is red.
A large bowl contains 100 jelly beans, 8 of which are red.
Red wins, white loses. Which bowl do you choose?
(Denes-Raj & Epstein, 1994, pp. 820ff.)
The majority of participants (82%) chose the large bowl in at least 1 out of 5 draws. This problem can be understood as the substitution of an easy question for a hard question, too. The easy question reads: ‘Which bowl contains more of the red jelly beans?’ And it is answered immediately by System 1: ‘The large bowl.’ The original question is a hard one: ‘Which bowl contains a higher percentage of red jelly beans?’ To answer this question, one needs to calculate a ratio. It is a task for System 2.
The third kind of error: System 2 might lack knowledge of appropriate rules for checking the correctness of System 1 responses. Statistical illiterateness is a classic example. Physicians were given the following task.
If a test to detect a disease whose prevalence is 1/1000 has a false positive rate of 5%, what is the chance that a person found to have a positive result actually has the disease, assuming you know nothing about the persons symptoms or signs? (Casscells, Schoenberger, & Graboys, 1978)
Only 18% of medical staff and students gave the correct answer. If you don’t know, how the false positive rate is calculated, then you give an intuitive answer which is provided by System 1. That is, you’re answering an easy question, for example: ‘What is the difference of 100% and 5%?’ You were originally asked a hard question. If you do the calculation properly, you get the correct answer, which is ‘a chance of about 2%’.
The fourth kind of error: Even if System 2 checks the intuitive response of System 1, it might happen that System 2 uses what has been called ‘contaminated mindware’ Perkins, 1995, p. 13; Stanovich, 2011, pp. 102–104; Stanovich et al., 2008). System 2 might use faulty rules, misleading information, inappropriate procedures, and deficient strategies. Consider the illusion of skill in share trading.
Overconfident investors overestimate the precision of their information and thereby the expected gains of trading. They may even trade when the true expected net gains are negative.
(Barber & Odean, 2001, p. 289)
Again this can be considered the substitution of questions. One question is: ‘Do I have information that suggests selling share A and buying share B?’ You can think about it using your System 2. The more you do so, the more you become confident in your decision, which is now rationally justified. But the most important question to answer is somewhat different: ‘On balance, do I expect positive net gains from selling share A and buying share B?’ System 2 sometimes answers the wrong questions, too.
In summary, we get a picture of different levels at which errors might occur (cf. Stanovich, 2011, pp. 95–119): System 1 uses a heuristics rule of thumb in an inapt environment, System 2 fails to check System 1, System 2 fails to override System 1, System 2 lacks rules or strategies to check System 1, or System 2 uses flawed rules or strategies. All these errors can be described as substitutions of questions. Either System 1 answers an easy question instead of a hard question, or System 2 answers a hard question with unsuitable means.
4. Application to fallacies
Now that I have traced the sources of thinking errors form a dual-process perspective, let me demonstrate how this idea can be applied to traditional fallacies.
Fallacies are substitutions of easy questions for hard questions. The easy questions are answered by System 1 in an intuitive way. The hard questions require some effort and analytical thinking by System 2. A fallacy occurs when System 2 is not alert enough or when System 2 applies faulty rules and strategies. Consider ‘Affirming the consequent’ as an example.
(1)
Affirming the consequent
If it rains, the streets are wet.
The streets are wet.
———————————-
Therefore, it rains.
Hard question: Is the argument logically valid?
Easy question: Is there a strong correlation between rain and wet streets?
System 1 can answer the easy question immediately: ‘Is there a strong correlation between rain and wet streets?’ It is part of our daily experience that if the streets are wet, it usually is because of the rain and not because someone spilt out water on the streets. Thus, System 1 gives an intuitive answer based on experience. And indeed, answers like these help us in our daily lives. It’s sensible to take an umbrella with you, when the streets are wet. Even if the streets might theoretically be wet for other reasons than rain.
But the original question was, whether the argument is logically valid. In order to answer this question, one needs to know the definition of ‘logically valid’ and apply it to the logical structure of this argument. Only then, after some mild effort, one arrives at the answer that it is not logically valid. The logical fallacy of affirming the consequent consists in not answering the hard question: ‘Is the argument logically valid?’ There are two main sources of error here. Either System 2 fails to check the intuitive answer of System 1 (lack of awareness), or System 2 does not know the meaning of ‘logical validity’ and, therefore, is not able to correct the intuitive answer (lack of knowledge).
(2)
Argumentum ad misericordiam
‘Could you please grant me an extension to complete my thesis?
My dog just died and I didn’t make it in time.’
Hard question: Does the student meet general criteria for granting the extension.
Easy question: Do I feel pity for the student (or the dog)?
Some students are very good at finding heart-breaking reasons for not being able to meet deadlines. Whatever triggers strong emotions, is likely to trigger a substitution of questions. The feeling of pity strikes one without effort. Emotions are a part of System 1. One can easily answer the question: ‘Do I feel pity for the student (or the dog)?’ In contrast, it is hard work for System 2 to establish general criteria for granting an extension. And it takes some effort to check whether the student really meets those criteria. Thus, the hard question is: ‘Does the student meet general criteria for granting the extension?’ It is much easier to grant an extension on the basis of pity than on the basis of general criteria. The argumentum ad misericordiam usually exploits a lack of willpower. In the light of heart-breaking reasons, one may find it inappropriate to insist on a list of criteria, despite the fact that one thinks extensions cannot be granted on the basis of pity.
(3)
Post hoc, ergo propter hoc
The computer worked fine until I installed the latest Windows update.
The update crashed my computer.
Hard question: Is there a causal link between the update and the crash?
Easy question: Is there a temporal link between the update and the crash?
It is very hard to establish a causal relation between two events. In order to answer the first question, one would have to run an experiment and show that this update always crashes any comparable computer. It is a task for System 2. Yet a causal relation implies a temporal relation: First update, then crash. Consecutiveness is a necessary but not a sufficient condition for causality. However, it is easy to perceive consecutiveness. Thus the second question can be answered swiftly by System 1: ‘Is there a temporal link between the update and the crash?’–‘Yes.’
The fallacy occurs when the answer to the easy question is mistaken for an answer to the hard question. This might happen if one is stressed about the crash and does not have the time to think analytically about the issue (lack of awareness), or if one does not know how to proof a causal relation between update and crash (lack of knowledge), or if one has a prejudice against Microsoft (contaminated mindware).
5. Conclusion
Traditional fallacies, such as affirming the consequent, argumentum ad misericordiam, or post hoc, ergo propter hoc, can be viewed as substitutions of questions. A fallacy occurs whenever one substitutes an easy question for a hard question without good reason. Easy questions can be answered fast and without effort; hard questions are characterized by them being answered slowly and with effort.
Conceptualizing fallacies this way opens a venue for applying dual-process accounts of reasoning to traditional fallacies. Cognitive processes in System 1 are fast, automatic, and effortless; cognitive processes in System 2 are slow, controlled, and effortful. This results in System 1 answering the easy question first. System 2 should check and correct the easy answer, where necessary. However, it may fail to do so for quite different reasons: (a) System 2 might fail to check the first response because of a lack of awareness, (2) it might detect an error but fail to override this response, or (c) it might not know how to check and correct the first response, and (d) sometimes it uses flawed rules and strategies to fulfil this task. All four kinds of thinking errors result in fallacies.
Acknowledgements
In memoriam of Thomas Becker, a great teacher and an encouraging supervisor. I would like to thank Hans V. Hansen for providing valuable hints and feedback on my talk. All shortcomings remain my own.
References
Barber, B. M., & Odean, T. (2001). Boys will be boys: Gender, overconfidence, and common stock investment. The Quarterly Journal of Economics, 116(1), 261–292. doi:10.1162/003355301556400
Casscells, W., Schoenberger, A., & Graboys, T. B. (1978). Interpretation by physicians of clinical laboratory results. New England Journal of Medicine, 299(18), 999–1001. doi:10.1056/NEJM197811022991808
Curtis, G. N. (2008). Fallacy files: Question-begging analogy. Retrieved from http://www.fallacyfiles.org/qbanalog.html
Denes-Raj, V., & Epstein, S. (1994). Conflict between intuitive and rational processing: When people behave against their better judgment. Journal of Personality and Social Psychology, 66(5), 819–829. doi:10.1037/0022-3514.66.5.819
Evans, J. S. B. T. (2008). Dual-processing accounts of reasoning, judgment, and social cognition. Annual Review of Psychology, 59(1), 255–278. doi:10.1146/annurev.psych.59.103006.093629
Evans, J. S. B. T., & Stanovich, K. E. (2013). Dual-process theories of higher cognition: Advancing the debate. Perspectives on Psychological Science, 8(3), 223–241. doi:10.1177/1745691612460685
Frederick, S. (2005). Cognitive reflection and decision making. Journal of Economic Perspectives, 19(4), 25–42. doi:10.1257/089533005775196732
Jackson, S. (1995). Fallacies and heuristics. In F. H. van Eemeren, R. Grootendorst, J. A. Blair, & C. A. Willard (Eds.), Analysis and Evaluation. Proceedings of the Third ISSA Conference on Argumentation, Volume II (pp. 257–269). Amsterdam: Sic Sat.
Kahneman, D. (2011). Thinking, fast and slow. London: Allen Lane.
Mercier, H., & Sperber, D. (2011). Why do humans reason? Arguments for an argumentative theory. Behavioral and Brain Sciences, 34(2), 57–74. doi:10.1017/S0140525X10000968
Müller-Lyer, F. C. (1896). Zur Lehre von den optischen Täuschungen: Über Kontrast und Konfluxion. Zeitschrift für Psychologie und Physiologie der Sinnesorgane, 9, 1–16.
O’Keefe, D. J. (1995). Argumentation studies and dual-process models of persuasion. In F. H. van Eemeren, R. Grootendorst, J. A. Blair, & C. A. Willard (Eds.), Perspectives and Approaches. Proceedings of the Third ISSA Conference on Argumentation (University of Amsterdam, June 21-24, 1994) (pp. 61–76). Amsterdam: Sic Sat. Retrieved from http://www.dokeefe.net/pub/OKeefe95ISSA-Proceedings.pdf
Perkins, D. N. (1995). Outsmarting IQ: The emerging science of learnable intelligence. New York: Free Press.
Stanovich, K. E. (2011). Rationality and the reflective mind. New York: Oxford University Press.
Stanovich, K. E., Toplak, M. E., & West, R. F. (2008). The development of rational thought: A taxonomy of heuristics and biases. Advances in child development and behavior, 36, 251–285.
Walton, D. N. (2010). Why fallacies appear to be better arguments than they are. Informal Logic, 30(2), 159–184. Retrieved from http://ojs.uwindsor.ca/ojs/leddy/index.php/informal_logic/article/view/2868
You May Also Like
Comments
Leave a Reply