ISSA Proceedings 1998 – Argumental Deduction: A Programme For Informal Logic

• by: Hans V. Hansen - Brock University

1. A remark on logical practices
The business of logic is to provide us with the wherewithal for the evaluation of arguments. Not everyone will agree with so blunt a statement but most will accept it as close enough to the truth insofar as logic figures in argumentation and argumentation theory.
I want to begin by looking at some of our logical practices. By a ‘logical practice’ I mean a logical method, even if it is only loosely defined, that is used more or less widely.
Consider first propositional logic set up as a natural deduction system. This is one of our logical practices. With this method we identify an argument’s premises and conclusion, write them in the syntax of propositional logic and then, by as many applications of valid inference rules as needed, we write a series of sentences the last of which is the argument’s conclusion. If we are successful we have a proof that the conclusion follows logically from the premises, i.e., that the argument is valid. Using the Venn diagram method for testing syllogisms is another of our logical practices. We map only the argument’s premises on the diagram and then examine it to see whether the given conclusion is present. The syllogism is valid just in case expression of the premises on the diagram is at once an expression of the conclusion too.
As a last example of one of our logical practices, think of informal logic. Not a few informal logicians teach that an argument is good only if the premises satisfy three conditions. One of these conditions is that they must be acceptable. The others are that the relationship between the premises and the conclusion must be such that the premises are relevant to the conclusion, and sufficient for the conclusion.
What these three kinds of logical practice, and some others, have in common is that they seek to evaluate arguments by examining the relationship between an argument’s premises and its conclusion directly. Each method requires that we determine whether the conclusion follows from the premises; that is, given the premises, the question is “by the standards in use, can the conclusion be said to be a logical consequence of the premises?”. It might not true. Consider, for example, the practice of logical analogies.

In evaluating arguments by logical analogy we proceed as follows:
A target argument, H, is presented for evaluation. A familiar argument, B, known to be a bad argument, is held to be structurally similar, or parallel, to argument H. Hence, H is a bad argument. For example, let the argument to be evaluated be

No liberals are conservatives
All liberals are supporters of socialized medicine
So, No conservatives are supporters of socialized medicine

The logical badness of this argument is demonstrated by the following analogous, and obviously bad, argument.

No historians are logicians
All historians are clever
So, No logicians are clever

Of course, although this is not much stressed in the literature, arguments can also be shown to be good by the method of logical analogy.

The point I want to make here, however, is that the practice of using logical analogies to evaluate arguments is quite dissimilar to the three practices I described earlier. The analogical method does not ask whether the conclusion follows from the premises according to a set of norms for ‘following from’. At least it does not address this question directly. Rather, the method of logical analogies sorts arguments whose logical value is not obvious into good or bad, according to whether they are analogous to arguments taken to be good, or bad. Hence, by the method of logical analogy, the question of whether the conclusion follows from the premises is decided indirectly: if the argument is analogous to a logically good argument, then the target argument is a good one too, and we infer that its premise-conclusion relation is in order; if the target argument is analogous to a bad argument, it is also a bad argument, and we infer that the conclusion does not follow from the premises (according to the relevant standards).[i]

2. Aristotle’s method
In the Prior Analytics Aristotle invented formal logic. He not only identified a class of valid syllogisms, he also gave a systematic proof of the validity of each of them. Briefly outlined, his method was to identify four first figure syllogisms which were obviously valid, and then prove that the other non-obviously valid syllogisms in the second and third figures were valid by showing that they could be reduced to one or another of the first figure syllogisms. Reduction to the first figure is accomplished either (a) by weakening the premises of the syllogisms being reduced, or
(b) by strengthening its conclusion, or
(c) by argument transposition.
Here ‘weakening’ means replacing a premise by its converse: I and E propositions convert without restriction, A propositions convert by limitation, i.e., SaP – PiS, but not vice versa (Corcoran 1983). Here is an example.

The reduction reads from right to left. Camestres, a second figure syllogism, is being reduced to the first figure syllogism, Celarent. The first move is from (iv) to (iii) where the minor premise has been converted from ‘CeB’ to ‘BeC’. The second move is from (iii) to (ii) where the conclusion has been converted (‘CeA’ to ‘AeC’). Finally, in (i), (ii) has been rewritten in conventional form so it is easily recognizable as Celarent.[ii] This constitutes a proof of the validity of Camestres in Aristotle’s system. The whole proof of all the valid syllogisms is largely encoded in the Medieval mnemonic, “Barbara, Celarent …”.

Aristotle is aware that valid syllogisms may reduce to invalid syllogisms as well as valid ones (Corcoran 1983). For example, Camestres might be reduced to

Camestres
BiA             AaB
CeB
CeB
CeA
CeA

The syllogism on the left is invalid. Invalid syllogisms, however, only reduce to other invalid syllogisms whereas second and third figure valid syllogisms reduce to at least some valid first figure syllogisms. The other kind of argument reduction Aristotle employs we may call an indirect method; it uses argument transposition. For example, on one of the third figure syllogisms, Bokardo, one performs the following operation. Mutually exchange the positions of the major premise and the conclusion, and negate them both. The
result is:

Again, I write the reductions from right to left. Bokardo is stated at (iii); at (ii) the transposition is made, and at (i), (ii) is re-lettered to be clearly identifiable as Barbara.

Let us make a few summary points about Aristotle’s method of reduction.
1. Some arguments – the perfect four – are taken as good arguments; they are not demonstrated as good by the method of reduction, but assumed as good, and needed for the method to work.
2. The method works by relating arguments whose logical status is unclear to arguments that are taken as logically good.
3. This ‘relating’ is done by argument reduction; that is by ‘weakening’ the premises, ‘strengthening’ the conclusion, or by argument transposition. Lastly,
4. it is a feature of Aristotle’s syllogistic reduction system that non-basic good arguments reduce to both good and bad arguments whereas bad arguments reduce only to other bad arguments.

3. Generalizing Aristotle’s idea
Aristotle’s reduction system is a system of argumental deduction. Such systems contrast with sentential deduction systems. Corcoran explains the difference as follows.

Opposed to the sentential deductions (which are lists of sentences) there are those which are lists of arguments. Systems which consist entirely of lists of arguments are called argumental deductive systems. … In creating an argumental deduction one does not start with premises and proceed to a conclusion but rather one takes ab initio certain simple arguments and constructs from them, line-by-line, increasingly complex arguments until the argument with desired premises and conclusion is reached. In argumental systems the rules produce arguments from arguments (not sentences from sentences) (Corcoran 1974: 176).

With this distinction in hand, the observations made earlier about our logical practices can be restated. Our dominant logical practices are methods of sentential deduction. (The term ‘statemental deduction’ is preferable for us, since we will be concerned with natural language argumentation.) Aristotle’s system of syllogism reduction, however, is a method of argumental deduction. Argument by logical analogy should also be thought of as a kind of argumental reasoning since it turns on evaluating an argument by comparing it to another argument. Logical analogies do not, however, seem to be a kind of argumental deduction.[iii]

4. Johnson’s intuition
Let us now turn to an important point made by Ralph Johnson. In his essay on theories of evaluation Johnson lists a number of intuitions which he thinks any worthwhile theory of rational argumentation must accommodate. One of these is that “arguments exist in a continuum from strong to weak” (Johnson 1992: 149). Johnson explains:
A theory of evaluation that accommodates this intuition must have more possibilities than just good and not-good. It should provide a spectrum with points along the way. It should turn out that arguments can be very strong, strong, moderately strong, weak, poor, etc. (Johnson 1992: 149).
I agree with Johnson on this point. Strange it is that automobiles, students’s essays, works of art etc. – all human artifacts – are ranked from the abysmally abominable through a fair number of intermediate grades right up to the perfectly wonderful, and that arguments aren’t. Or, rather, we should say, that although we do recognize the fact that arguments exist in a continuum from bad to good, our extant logical practices, both formal and informal, provide only scant guidance on how to incorporate this fact into a logical theory.

5. Two senses of ‘informal logic’
Since its inception a number of distinct, albeit related, senses of ‘informal logic’ have been advanced. Here I shall be concerned only to distinguish what I will call the wide and the narrow senses of ‘informal logic’.

In the wide, or dialectical, sense of ‘informal logic’ the term denotes an approach to natural language argumentation that takes these three criteria as definitive of a good argument.

(C1) The argument’s premises must be relevant to the conclusion
(C2) The argument’s premises must be sufficient for the conclusion
(C3) The argument’s premises must be acceptable

Here premise acceptability is considered to be a logical requirement,[iv] indicating that ‘good argument’ is being construed as ‘good dialectical argument’. There is reason to take this approach since public arguments – most of them, at least – fit in a dialectical or rhetorical context, even if these contexts are sometimes rather indefinite. And it is precisely such arguments that the informal logicians want to tackle and make pronouncements about.
However, in order for an argument to be dialectically good it must first be logically good, and in determining logical goodness we ignore for the most part the question of whether the premises are acceptable. ‘For the most part’ because questions of premise acceptability nearly all fall under the heading of epistemology. The logician, qua logician, can ask some questions about the premises independently of their relation to the conclusion; namely, whether they form a consistent set, and if they don’t, they can be deemed unacceptable.[v] But this is as far as logic can go in pronouncing on premise acceptability.
Hence, shorn of the premise acceptability requirement, we have ‘informal logic’ in the narrow or logical sense. The project of informal logic in this narrow sense is to see how far we can develop logic without availing ourselves of the plentiful resources of logical form as it figures in formal logic. Our main resources will be the intuitive notions of ‘relevance’ and ‘sufficiency’.
These then are the three points of departure: Aristotle’s method of argumental reduction, Johnson’s intuition about the continuum hypothesis, and the narrow version of informal logic just explained.

6. Implicit uses of argumental deduction
Earlier I claimed that the method of logical analogies was one of our logical practices, albeit perhaps an imperfect one, and that it was a kind of argumental reasoning. I now want to suggest that other elements of argumental reasoning, are embedded in some of our thinking about good and bad arguments.
Sometimes we speak of improving or weakening arguments; for example, we say, “you could improve your argument by getting more information” or “the argument is weaker if the authority turns out to be unreliable”. This is consistent with Johnson and Blair’s remark that “Rarely is an argument so good that it cannot profit from criticism and seldom is an argument so bad that it cannot be improved by criticism” (Johnson and Blair 1993: 43). Implicit in this view is the idea that an argument is something you can work on – add something to, change a part of, leave something out of – and end up with an improved version. From the argumentation theorist’s point of view this observation is entirely correct but from the logician’s point of view it is objectionable. We would do well here to hang on to these two necessary conditions of argument identity:

Argument A = argument B only if (i) the premises of A = the premises of B and (ii) the conclusion of A = the conclusion of B.

If we stick to the concept of argument identity, then we see that an argument cannot be changed any more than the number two can be changed; therefore, strictly speaking, talk of improving arguments (or weakening them) won’t do at all. But, what then is going on when we are ‘improving’ our arguments? The answer is that we are composing or discovering new arguments that we believe are better than the argument we began with. Every ‘replacement’ of one proposition by another ‘in an argument’, every ‘deletion’ and every ‘addition’ is really, from this point of view, the creation of another argument. We are already, then, in the habit of making new arguments stemming from other arguments.

Some of the elements needed for an argumental logic are most readily obvious in the rules we give for good inductive and analogical arguments (not arguments by logical analogy).

In analogical arguments two subjects are compared. Common properties are identified along with a projected property. A simple rule of analogical arguments is that argument strength is a function of the number of common properties that are relevant to the projected property. Whereas we might be inclined to say that the argument is improved by identifying more common properties, what we really should say is that the increments in common properties leads to a sequence of arguments, each one stronger than the one before it.

The sequence is, of course, extendable as more common properties are adduced.

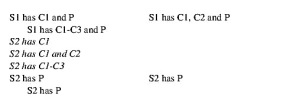
Another rule for analogical arguments is that their strength is a function of the sweep of their conclusions: the less sweeping the conclusion, the stronger the argument. This consideration could give us a sequence like this:

S1 has C1-C3 and P
S1 has C1-C3 and P
S1 has C1-C3 and P
S2 has C1-C3
S2 has C1-C3
S2 has C1-C3
Certainly S2 has P Very probably S2 has P Probably S2 has P

Similarly, it is easy to see that sequences of inductive generalizations, both universal and statistical, can be constructed in a very similar way. Each time another white swan is observed the size of the sample is increased, and a new argument is added to the series; and every weakening of the conclusion is also a new argument.
Other elements of argumental deduction may be found in a nascent state in some of our other logical distinctions. For example, another way we can strengthen premises is by making changes within modalities.

For example,
Epistemic: believes p, has pretty good reason to believe p, is justified in believing p, knows p
Alethic: possibly p, contingent p, necessarily p
Deontic: permitted that p, obligatory that p
Quantitative: some, most, all

Statements also increase in strength as their probability increases, and since we can express degrees of probability very precisely, we could write a fine-grained series of arguments by increasing the probability little-by-little.
Still another way that we can write a stronger premise set is by adding more independent premises to it, making a new ‘convergent’ argument that exceeds the number of reasons (premises) of the original argument.

7. An intuitive system of argumental deduction
Based on these observations, let us consider a system of argumental deduction that is both informal and general. It will be informal because it eschews all considerations of logical form, although it will make use of several semantic concepts also used in formal logic.
And the system will be general because it is meant to have application to all kinds of natural language arguments, not just syllogisms, or inductions, or relational arguments, etc. Moreover, whereas one can think of Aristotle’s reduction system as an axiomatic argumental deductive system – with the perfect four being the axioms – the system to be developed here is more likely to be termed a natural deduction argumental system (since no particular arguments will be taken as axiomatic).

The core idea is very simple. We string together sequences of arguments such that their relative strength in relation to each other are indicated by their position in the sequence. Let us adopt the convention of writing our series such that the very weakest argument is on the left, the very strongest on the right, and the ones in between are placed in an ascending order of strength from left to right. Thus, in general, for any argument in the series, the arguments on its right are stronger than it, and the ones to its left are weaker than it.

How will this work? To write a stronger argument, take any argument and write another argument to the right of it whose premises have greater sufficiency in relation to the given conclusion than the original argument; this second argument will be stronger than the original one. Or, leave the premises as they are but weaken the conclusion and this too will result in a stronger argument. For example,

A1 –  A2 –  A3
Some men are mortal Most men are mortal Most men are mortal
Socrates and Aristotle Socrates and Aristotle Socrates is mortal are mortal are morta

Here A2 is stronger than A1 because the premise in A2 is stronger.
A3 is stronger than A2 because the conclusion of A3 is weaker than that of A2. Obviously, the series A1-A3 is extendable in either direction.

Read from left to right the series A1-A3, shows arguments of increasing strength. Read from right to left it shows arguments of decreasing strength, and here it is an argumental reduction sequence.

In general, any argument can be reduced to any of the arguments to its left. Moreover, for any series of arguments,

A1, A2, A3, A4, A5, A6, A7, A8, A9, A10, etc.

if, say, A7 is a logically good argument, then the ones to the right of it, A8-A10, etc, will be logically good argument also; and if A4 is a logically bad argument then the ones to the left of it will be logically bad arguments too. We may classify A5 and A6 as neither good nor bad, but middling, with A6 being the stronger.

We have to pause momentarily to clarify how we are to understand the relation ‘argument A is stronger than argument B’. In the logical sense, one argument is stronger than another if it provides more support for its conclusion than another argument provides for its conclusion (supposing, of course, that the premises in question are true or acceptable). For example, one might hold that the cosmological argument for God’s existence is stronger than Jones’s argument against the abolition of slavery, or that a particular argument for free trade is stronger than a particular argument against it.
Whenever we adjudicate issues from a purely logical point of view we do so on the basis of comparative logical strength and nothing else. However, this comparative sense of ‘stronger than’ is too wide for the purposes of our present project.

In a narrower sense of ‘argument A is stronger than argument B’ we mean that the stronger argument is an improvement or development of a weaker argument; the weaker argument lacks certain logical merits that the stronger argument has. It is possible to take an argument and ‘add to it’ (so to speak) to make it better, and then to make even more improvements again and again. This narrow sense of ‘stronger argument’ implies that there is some logical relation between two arguments when one is stronger than another such that the weaker argument can be obtained from the stronger argument. I call this the serial sense of ‘stronger argument,’ and will attempt a clearer statement of it in sec. 9.
The requisite skill in this kind of logic is to be able to write a  series correctly, with the arguments in ascending order of strength. Once this is done one can reduce any argument to any other on its left in the series.
Aristotle’s insights about argument reduction have here been generalized. Argument A reduces to argument B if the strength of A’s premises is greater than the strength of B’s, or the conclusion of B is stronger than the conclusion of A. In addition, Aristotle’s insight that good arguments also reduce to bad arguments is preserved in this approach because there will always be bad arguments to the left of good arguments. However, bad arguments can only reduce to other bad arguments since there are no good arguments to the left of bad arguments. The present approach does differ from Aristotle’s in one important respect. We are not identifying a subset of good arguments to which all other good arguments are to be reduce. This method presupposes that it will be possible to identify some arguments as good on independent grounds.
Moreover, Johnson’s intuition about the continuum hypothesis fits nicely with argumental deduction: every series of argument is also a continuum of arguments related to each other in terms of comparative logical strength. Perhaps, by restricting ourselves to the serial sense of ‘stronger than’, we have given the continuum hypothesis a narrower interpretation than Johnson anticipated but this is not inconsistent with the idea that arguments can also be ranked in the wider, comparative sense; although how this might be done is a problem that goes beyond the reach of our present project.

Finally, we have accomplished this much logic by relying only on the notions of ‘relevance’ and ‘sufficiency’. They are assigned distinct roles in argumental series. Relevance is the price of admission; an argument’s premises must be relevant to its conclusion if it is to be included in a series. Sufficiency determines seating-order; the more sufficient premises are with respect to a conclusion, the closer the argument sits to the orchestra (the further it is placed to the right in the series). We hasten to add and admit that there are no new insights or improved analyses of the concepts ‘relevance’ and ‘sufficiency’ provided by this approach; they are used at the at the same face value they have in other informal logic projects.

8. A general system of argumental deduction (System G)
System G is designed to provide a conceptual framework for constructing series in which to place arguments that occur in natural language argumentation. It attempts to define the concepts needed for constructing the series of arguments in which argumental deduction can be carried out. The most important concept developed is that of an ‘argumental series’ (Df9).

We begin by defining the relative strength of two sets of statements.

(Df1) A set of statements B is stronger than a set of statements A iff B entails A, and A does not entail B.

The motivating intuition here is that a stronger set of statements has greater scope, or sweep, than a weaker set and is therefore more likely to be false. Still, the definition falls prey to the standard paradoxes: if the statements in B are logically inconsistent and those in A are not, the definition is satisfied. There is a limitation, however.

A sequence of sets of statements will be transitive with respect to ‘stronger than’ only if any member of the sequence that is inconsistent is the last member of the sequence. If the last two members of a sequence were both logically inconsistent, for example, then the penultimate set would entail the final member, and the final member would not be stronger than its predecessor.
If the conjunction of the premises in A constitute a necessary truth, and those in B do not, then it is true that B entails A (because any set of statements entails a necessary truth) and it is true too that A does not entail B (since necessary truths do not entail non-necessary truths). This consequence is not unwelcome since contingent propositions provide better support for other continget propositions than do necessary truths.

Definition 1 is an ingredient in the definition of ‘stronger set of premises’.

(Df2) A set of premises, D, is stronger than a set of premises, C, iff
(i) D is stronger than C and
(ii) every member of D, either in combination with other members of D, or individually, is positively relevant to the conclusion of C.

We are on the way to defining ‘stronger argument’ (in Df4), and one of the ways that an argument can be stronger than another is by having ‘stronger premises.’ However, this cannot be understood simply as being a stronger set of statements. They must not only be that, they must also be a stronger set of statements that will serve as premises for the same conclusion as the weaker argument. This is what the second condition of Df2 attempts to ensure.

The other condition that affects argument strength relates to conclusions: the weaker the conclusion, the stronger the argument. Since ‘weaker than’ is the converse of ‘stronger than’ we have the following definition.

(Df3) For any sets of statements E and F, E is weaker than F iff F is stronger than E.

Incorporating Df2 and Df3, we define ‘logically stronger argument’ as follows.

(Df4) An argument H is logically stronger than an argument G iff either
(i) the premises of H are stronger than the premises of G or
(ii) the conclusion of H is weaker than the conclusion of G.

Now, let us add that
(Df5) Two or more arguments constitute a sequence (of arguments).

An argumental deduction is a special kind of sequence, one in which all the members of the sequence are related in a specifiable way. Such a sequence we will call a ‘series’ and tentatively define as,

(Df6) A series (of arguments) is a sequence of arguments such that every successor in the sequence is logically stronger than its predecessor.

But this won’t quite do, especially if we want to generalize on Aristotle’s methods of argument reduction that we looked at earlier (in sec. 2). One of those methods was reduction by argument transposition. An argument is a transpose of another if, and only if, the conclusion of the first argument is negated and replaces a premise in the second argument, and the evicted premise of the second argument is negated and is the conclusion of the first argument. In general,

A        A
B        not-C
C        not-B

for any number of premises, is what argument transposition brings about (recall the example of Bokardo, in sec. 2). Argument transposition figures in argument reduction and deduction, but the arguments are of equal logical strength; the one is not logically stronger or weaker than the other. This means that there is more than one way to write an argumental deductive sequence: one in which each successive member is stronger than the one before it, and one in which successive arguments have the same logical strength (see Hansen 1994).

Another consideration is that, in addition to argument transposition, there are argument reductions where it is misleading to say that the reduction is to a weaker argument. Aristotle’s example of a reduction from Camestres to Celarent is itself an illustration of this, for it involves only the conversion of E propositions, and statements of the form ‘SeP’ are neither stronger nor weaker than statements of the form ‘PeS’. We would not call such converse statements identical, but they are equivalent. Hence, we need to define a concept somewhat broader than ‘argument identity’. Let us say that two statements are equivalent if they entail each other; then (Df7) Argument K is equivalent to argument L iff every premise of K is equivalent to a premise in L, and vice versa, and (ii) the conclusion of K is equivalent to the conclusion of L.

We are now in a position to offer an improved definition of argumental series.

(Df8) An argumental series is a sequence of arguments such that for any two members of the sequence the successor is either
(i) logically stronger than its predecessor,
(ii) an argumental transpose of its predecessor, or
(iii) an argument equivalent to its predecessor.

This is the preferred definition of ‘argumental series’.
Given Df8 a number of rules about comparative argument strength can be given. I shall state only two of them. First, the rule for good arguments.

Rule GA: An argument Ai in a series S is a good argument iff there is an argument Ai in S, (to the left of Ai), and Ai-j is a good argument. A series itself does not decide which arguments are good. Argument reduction and deduction always depends on some arguments being taken as good on other grounds; hence, what this approach to logical evaluation allows is the making of comparative judgments in view of the assumption that some of the arguments in a series have been assigned a value. In other words, the rules give sufficient conditions for good arguments, not necessary conditions. Analogous considerations apply to the rule for bad arguments.

Rule BA: An argument Ai in a series S is a bad argument if there is an argument Ai+j in S (to the right of Ai), and Ai+j is a bad argument.

9. Conclusions
I am not advocating that argument evaluation in informal logic should proceed by actually writing long or short series of arguments and then carrying out a reduction. In a very few cases this might be helpful. However, realizing that it is possible to place every argument in a series gives us a perspective on relative argument strength that is instructive. Not only does argumental deduction allow for argument reduction, it also gives directions for argument construction; that is, it incorporates the principles for writing logically better arguments.
Earlier I distinguished between ‘informal logic’ in the wide and narrow senses. Our ultimate goal, of course, is to practice informal logic in the wide sense that includes the requirement that premises should be acceptable. With respect to argument series, some observations are possible in this regard.
In general, the stronger an argument’s premise set the less likely it is that it will be acceptable. The desire for logical strength pushes us rightward in our series but dialectical reality creates a leftward force. Hence, the argument that is likely to be successful in a dialectical context will be one that is a compromise between considerations of logical strength and premise acceptability. With regard to conclusions of arguments, in general, the weaker they are the stronger the argument is logically. Again, the need for logical strength pushes us rightward in argument series. But the weaker a conclusion is the less likely it is to have the required dialectical bite. That is, a weak conclusion may be established by a logically strong argument with acceptable premises but the conclusion may not be strong enough to do the work required. So, dialectical considerations also put a check on the weaknesses of conclusions.
Everything Aristotle could have dreamed of in terms of showing arguments valid, and more, has found a home in modern logic. One might say that first-order logic is a generalization of Aristotle’s insights about the syllogism if, that is, we view the syllogism as a kind of statemental deductive logic. However, if we consider Aristotle’s logic as an argumental deductive logic, then the present project is an attempt to generalize his insights about reduction, and extend them to non-syllogistic logic as well.

NOTES
[i] I am not forgetting that an argument’s having an invalid form is insufficient for convicting it of having no valid form, and hence for showing that it is invalid. The importance of this (the asymmetry thesis) is that it shows that the method of logical analogies is not an effective method; it does not show that it is not a useful method.
[ii] This last step is required neither by Aristotle nor by logic; it simply puts the argument in what we have come to think of as standard form.
[iii] The system developed below cannot accommodate logical analogies.
[iv] Johnson and Blair (1993: 62) say it is a logical requirement.
[v] Tapscott (1976: 80) defines ‘good argument’ as a valid argument with consistent premises

REFERENCES
Corcoran, J. (1974) “Remarks on Stoic deduction,” In : J. Corcoran (ed.) Ancient Logic and its Modern Interpretations. Dordrecht: Reidel. pp. 169-81.
Corcoran, J. (1983) “Deduction and reduction: Two proof-theoretic processes in Prior Analytics I,” J. of Symbolic Logic 48: 906.
Hansen, H. V. (1994) “Reductio without assumptions?” Logique & Analyse 147-48: 329-37.
Johnson, R. H. (1992) “The impact of the continuum hypothesis on theories of evaluation,” In: F. H. van Eemeren, R. Grootendorst, J. Antony Blair, C. A. Willard (eds.) Argumentation Illuminated. Amsterdam: Sicsat. pp. 148-58.
Johnson, R. H., and J. A. Blair (1993) Logical Self-Defense, 3rd ed. Toronto: McGraw-Hill Ryerson.
Tapscott, Bangs L. (1976) Elementary Applied Symbolic Logic. Englewood Cliffs: Prentice-Hall.

You May Also Like

ISSA Proceedings 2006 ~ The Criminal Abduction Paradox

ISSA Proceedings 2006 ~ A Discussion Of Habermas’ Reading And Use Of Toulmin’s Model Of Argumentation

ISSA Proceedings 2006 ~ The Rules Of The Critical Discussion And The Development Of Critical Thinking

ISSA Proceedings 2006 ~ An Analysis Of Preschool Hebrew Speaking Children’s Arguments From The Perspective Of The Pragma-Dialectical Model

ISSA Proceedings 2006 ~ Putin’s Terrorism Discourse As Part of Democracy And Governance Debate In Russia

ISSA Proceedings 2006 ~ Cultural Differences In The Persuasiveness Of Normatively Strong And Normatively Weak Expert Evidence

Comments