ISSA Proceedings 1998 – Using Argumentation Analysis To Examine History And Status Of A Major Debate In Artificial Intelligence And Philosophy
No comments yet 1. The Problem
1. The Problem
My primary goal today is to introduce you to a pioneering project undertaken to see how extensive mapping of arguments can be accomplished and whether such a mapping would be useful to students, teachers, and scholars. Why would you want to map an extensive argument? Let me start with a hypothetical story. In the 1930s Alan Turing, the great British mathematician, invented the ideas on which the modern computer is based. In 1950, he wrote, “I believe that at the end of the century the use of words and general educated opinion will have altered so much that one will be able to speak of machines thinking without expecting to be contradicted.” He certainly thought the computers would be able to think. However …. there are less than two years left before the end of the century. Unfortunately, Turing died in 1954 at the age of 42. Suppose he came back from the dead after 44 years to find out whether his prediction had come true. Suppose he asked you, “What’s happened since I died? Was I right? Does everybody agree that computers can think?”
In the first place we could tell him that he certainly should have expected to be contradicted. That almost 400 scholars have engaged in a 48-year argument that he started. That the argument was worldwide. That it has taken place in almost 300 journals and books and consists of more than 800 major “moves” – claims and rebuttals and counterrebuttals. He would find out that some of the greatest physicists, philosophers, computer scientists, and psychologists in the contemporary world have taken part in it.
Suppose Turing said: “Right now I don’t have time to read 300 journals and books. What is the status of the argument? Where does it stand now?” Stop for a moment. How would you give him a serious answer? Suppose you managed to answer his question. Then suppose he asked another: “Where can I get an overview of the history of the arguments so I can decide which I want to read.” Where would you direct him?
2. The Problem As We Saw It
For great debates like this one about machine intelligence, there is:
– no comprehensive map of this major debate
– no way to get an up-to-date briefing on its current status
– no way to link positions to rebuttals (so that proposed refutations of data and positions can be easily compared)
– no efficient way to navigate through the argument
– no way to visually inspect its structure and direction
These are also the problems of every beginning student in any major subject-matter debate. And these problems are not only true of the artificial intelligence debate but also of most of the great discussions in which humanity is involved. While the argumentation maps I will talk about today show the substance of this decades-long, worldwide debate, I will not so much focus on the substance of that particular argument. Rather, I want to discuss with you the argumentation analysis format we developed, the implications that our maps have for the study of argumentation analysis, the problems we encountered, and the kinds of solutions we came up with.
I should add an historical note here. Credit must go to Stephen Toulmin who, as far as I know, developed the modern ideas of argumentation analysis in 1957. I worked in the mid-80s on a variety of graphic approaches to mapping extensive argumentation. A chapter of my 1989 book, Mapping Hypertext, is devoted to the progress I made. But in the end I felt I hadn’t quite got a useful enough approach. Four-and-a- half years ago I took up the problem again when I went to Stanford.We wanted to map a major philosophical argument. The debate Turing started qualifies, as it involves one of the major questions about which human beings puzzle, worry, and debate – our identity. Who are we? While the history of this debate goes back at least to Hobbes, Leibniz, and Descartes, as I said, the modern debate starts with Turing’s 1950 article in the journal Mind.
Our goal was to map a whole argument and a big one, not some little piece of a broader debate. The Turing argument was an ideal choice. It turned out to be an even bigger challenge than I thought. The debate was far more extensive than I knew or than what usual book-length summaries indicated. But it was an ideal testbed for the visual methodology we were developing. And we faced the challenge of designing a useful tool–simple enough to be educationally sound yet detailed enough to help scholars.
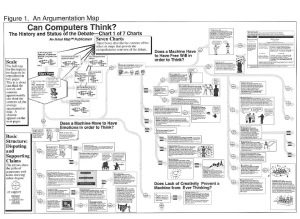
What do the maps look like? Figure 1 shows a complete map and figure 2 shows detail.
3. Basic Structure of Argumentation Maps
The basic framework of our mapping generally follows Toulmin.
3a. Major topics of the debate
One of the consequences of our taking on such a large, sprawling argument was that we needed to subdivide it into different issue areas. Debates frequently divide into topic areas which can be shown as regions in the mapping of the debate by putting them all together in one area and giving them a title. The example here shows the initial claims boxes of three regions, identified with the questions in bold face. Table 1 lists the issue areas. It shows the breadth of the more than 50 philosophical issues that have become involved in the debate over Turing’s question. It provides a kind of table of contents or subject index of the issues. Within each issue area, the arguments are presented chronologically.
3b. Focus box
The focus box introduces and summarizes the core dispute of each issue area, sometimes as an assumption and sometimes as a general claim with no particular author. The lowest-numbered box in each issue area is an introductory focus box.
3c. Claims
Debates start with claims, which have been defined by Toulmin as “assertions put forward publicly for general acceptance with the implication that there are underlying ‘reasons’ that could show them to be ‘well founded’ and therefore entitled to be generally accepted.” (Toulmin et. al., l979) Claims as we have written them are brief summaries, often accompanied by explanatory illustrations.
Some readers have been thrown off in expecting the claim boxes to be abstracts of published works. But claims summarize individual arguments. As such, a given published article may be broken down into numerous claims on the maps; alternately, a given claim may draw on information in several published chapters and articles. Each claim is connected to the next by one of three links: supported by, disputed by, or interpreted as.
3d. Supported by
We defined the “supported by” relationship slightly differently than Toulmin. These are arguments that uphold or defend another claim. Examples include: supporting evidence, further argumentation, thought experiments, extensions or qualifications, and implemented models.
3e. Disputed by
These are charges made against another claim. Examples include: logical negations, counterexamples, attacks on an argument’s emphasis, potential dangers an argument might raise, thought experiments, and implemented models.
3f. Support and dispute carry a range of meanings
Support and dispute are used in an argumentative sense rather than in a strict logical or epistemic sense. They structure the map into chains of agreement and disagreement where claimants respond to one another in a variety of affirmative and negative way. As such, the relations of support and dispute cover a wide range of cases, which fall into “fuzzy categories” or “families” of supportive and disputative responses.
3g. Interpreted as
Sometimes an argument is reframed by one of the disputants. If there was a distinctive reconfiguration of an earlier claim, we used this icon.
3h. Anticipated by
Where this phrase appears in a box, it identifies a potential attack on a previous argument that is raised by the author so that it can be disputed.
3i. Links as arrows direct the eye
After experimenting with a number of formats, we decided to use arrows to show the paths of arguments, with icons showing whether the relationship was one of support, dispute, or interpretation. The directionality of a link, represented by an arrow, represents the direction in which the reader should read the claims for maximal effectiveness. The arrows direct the eye. Thus, links do not necessarily correspond to direct evidential support, logical negation, or any more crispy defined logical relation (though in particular cases a link may be any one of these). I should point out that we sometimes include what Toulmin would call grounds, warrants and backing in our claim boxes. We did this primarily to avoid more of a tangle of boxes and arrows than we already had.
3j. Rebuttals and counterrebuttals
The rebuttal presents the possible exceptions or objections to the claim. There is no such thing as a debate without at least one rebuttal. And we followed that guideline as a criteria for choosing arguments to map.
Debates then continue through a series of contributions that dispute previous claims and other rebuttals. The counterrebuttals may or may not be made by the original claimant.
4. What’s the Answer? Can Computers Think?
The argumentation maps do not attempt to evaluate the arguments summarized. They map the debate without taking a stand. They are, as much as possible, neutral. It is left to readers to be the jury, to evaluate the “weight” of the arguments and evidence and draw their own conclusions. Many students have been frustrated by this. Indeed many scholars who have seen the maps say, “So, what’s the answer?” The maps do not provide the answer. Hopefully they do not even reveal the mapmakers’ views.
Of course, the maps are to some extent interpretive. In writing and linking arguments, we had to condense incredible amounts of information, often on the basis of highly obscure or technical literature. We also had to make decisions about placement and emphasis. The way these maps organize the debate is not necessarily the only possible organization, but it was carefully considered and weighed against alternatives. The argument summaries themselves, which is where the real dialogue takes place, stick closely to the words of the authors, the better to avoid interpretation.
5. Criteria for Inclusion of Arguments
Over the course of the project, we have developed 11 criteria for deciding whether to include a particular argument.
5a. Use published arguments
Only those arguments were included that have been published in an established print or electronic medium: journals (including reputable electronic journals and white papers), magazines, and books. Arguments made in Usenet newsgroups, electronic forums, e-mail exchanges, or in interpersonal debate were excluded as too ephemeral and as representing positions still in development. Such arguments will be excluded until they appear in a more established medium.
5b. Use arguments that lie within the scope of the map
The major claim – that machines can or will be able to think – determines the scope of these maps. Many threads of argument drift away from the central issue into such related territories as the mind-body problem, functionalism, and the philosophy of science. Such claims were set aside until a chance arises to map neighboring territories with maps of their own.
5c. Seek out the historically earliest or best-known version of an argument
When different authors make similar arguments, we chose the version which was either historically earliest, or the best-known version of the argument. When the best-known version is used, the historically earliest version is usually mentioned in a note. In the few cases in which differing versions of an argument are sufficiently unique or separately disputed, each is summarized separately.
5d. Avoid loosely drawn arguments
Sometimes an author makes an argument loosely, at the end of a paragraph, as an aside, or in a footnote. In general, such arguments are not included unless they are developed further in follow-up articles or are the focus of further debate.
5e. Avoid repetitive, nitpicking, or duplicative arguments
One goal of the maps is facilitation of productive debate. Ad hominem arguments, redundant rounds of back-and-forth, and tediously nitpicky arguments were left out.
5f. Avoid forbiddingly technical discussion
Highly technical arguments, which are based on extensive symbolic notation and formalisms, could not be represented with the cartographic conventions we developed, or at the scale we chose to work at. However, summaries of many technical and symbolic discussions were included. Only the most forbidding had to be excluded.
5g. Summarize the author’s published claim
Many authors hold views today that are different from those they expressed at the time they entered into the debate. We include authors’ claims as published. If an author later changed his or her position, and published the change, the new claim was included and the change of position was noted. But if no new contribution has been made, then the original published view stands.
5h. Avoid tentative arguments
It became clear as we wrote the summaries of the arguments that one current, tentative style of academic writing made it extremely difficult to understand exactly what was being argued. In some way, authors had to be definitive in their arguments to qualify for a spot on the map. To use a geographical analogy, a road or a lake or a mountain that “may exist” is rarely mapped.
5i. Include some historical arguments
In order to properly situate the debate in its historical context, we included a sampling of notable historical supports of contemporary arguments.
5j. Include some experimental results
To situate the debate in a context of concrete experimental and computational results, we included some implemented systems and empirical results. Again, we only included a small sample of such results, sticking to famous and notable computer models and experiments.
5k. Include a small sample of outrageous and humorous arguments
Some of the stronger and stranger claims were worth including just to liven things up and have some fun. Such claims also provide “targets” for what we anticipate will be lively threads of response.
6. Why are argumentation maps important to teaching?
The biologist Lewis Thomas has written, “College students, and for that matter high school students, should be exposed very early, perhaps at the outset, to the big arguments currently going on among scientists. Big arguments stimulate their interest, and with luck engage their absorbed attention… But the young students are told very little about the major disagreements of the day; they may be taught something about the arguments between Darwinians and their opponents a century ago, but they do not realize that similar disputes about other matters, many of them touching profound issues for our understanding of nature, are still going on, and, indeed are an essential feature of the scientific process.”
This is the overarching reason that we created these maps – to illustrate for students the dynamic nature of a debate that is active today.
6a. Watching Contemporary, Interdisciplinary, Global Debates Unfold
The intelligent machines debate is a prime example of the type of argument that benefits particularly well from argumentation mapping. From its beginning, the debate has been a truly interdisciplinary and global discussion, with philosophers, cognitive scientists, artificial intelligence researchers, and others joining in, from around the world. Nevertheless, great parts of the debate have taken place in journals that are isolated by the boundaries of particular academic disciplines. As a result, it has been difficult until now to see the structure of the debate as it unfolds.
Argumentation maps provide a picture, more detailed than previously available, of how such a vast debate can take place across disciplinary and geographic distances. By creating an accessible map of the conceptual territory our hope is to facilitate more global interdisciplinary debate, to bring the various sources to light, and to illuminate how the pieces of the puzzle fit together. Perhaps the very existence of the maps will provide incentive and opportunity for more interdisciplinary and international discussion.
In a world of global interdisciplinary discussion, effective communication and productive dialectical exchange are key. We need to elevate the coffee-house discussions and the Usenet dialogues into cooperative and productive exchanges that push our understanding forward. It is all too easy to repeat an argument that has already been made in a distant or obscure location, to talk past one another in the heat of conflict, or to ignore important context. Moving a serious debate forward requires a disciplined interdisciplinary and international dialectic.
6b. Work with Great Minds
It is of benefit to students to observe and engage with great minds at work. The Can Computers Think? arguments have attracted some of the greatest and most subtle minds of the 20th century. I could mention Herbert Simon, Nobel Prize–winning economist; Kurt Gödel, who with Turing was among the greatest mathematical minds of all time; Roger Penrose the great physicist; John Searle, former president of the American Philosophical Association; Herbert Dreyfus, one of the world’s leading Heidegger scholars; John McCarthy, who named the field artificial intelligence; and many more whom I don’t have time to list here.
6c. Learning philosophy dialectically
Argumentation maps illustrate the value of learning philosophy dialectically. Individual arguments are presented in clear summary form and are followed by chains, or threads, of dispute and support. By watching philosophers lock horns and wrestle in an interdisciplinary arena of open debate, readers can better appreciate the subtlety and complexity of the issues they themselves are struggling with.
The dialectical method has ancient roots and remains valuable today. Thousands of years ago Socrates grappled with the best minds of Athens in public debate, and Plato recorded those dialogues as a means of teaching philosophical concepts. Today, contemporary issues are battled out in televised forums and in Internet newsgroups, where everyone from big-name pundits to coffee-shop philosophers chew through issues in round after round of back-and-forth. Argumentation maps harness the full communicative and instructional power of dialectical exchange.
7. More specific educational possibilities
How can these maps aid education and, in particular, education in argumentation analysis? I am sure that many of you will come up with creative uses that we on the project have never thought of. But here are a few possibilities, using the Can Computers Think? series as an example, that we would offer for your consideration.
7a. Excellent hook for student interest
It is easier to get into a subject that has some connection to currently hot topics in the culture. The maps can be used to introduce questions of philosophy in a way that is attractive and compelling. Many students will have heard of the IBM computer Deep Blue that recently beat the human grandmaster champion at chess. The chess-playing arguments are represented appear on Map 3, Can Physical Symbol Systems Think?
 7b. Touches many subjects
7b. Touches many subjects
One of the important things about the Can Computers Think? debate is that it touches on so many of the ongoing topics in philosophy : the mind-body problem, consciousness, free will, etc. This permits the instructor to show how one set of arguments relate to other sets of arguments in related areas.
7c. Provide project opportunities in creative argumentation
Since the maps provide the thread of existing arguments and also show where they have ended (as of now), they provide the opportunity for assigning students to select one thread or topic of an argument and try to add to it with an original argument, or write a critical essay about it, or read the original sources of one or more issue areas and critique them. Since the maps clearly mark the frontiers of arguments, students have a chance to engage in real debates and contribute their critical assessments as well as new arguments.
7d. Save time and provide context
One graduate student in the philosophy of mind said to us: “These maps would have saved me 500 hours of time my first year in graduate school. For almost two semesters, I had to keep reading article after article without enough context to see how they fit in to the bigger picture. The maps would have made my whole experience 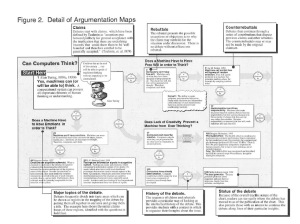 a much more rewarding one.”
a much more rewarding one.”
8. Other Topics
We are proceeding on maps of several other major debates and have proposals out for still others. We believe that this mapping approach will serve education by providing a general methodological tool and by providing authoritative maps in substantive areas.
 REFERENCES
REFERENCES
Horn, R.E. (1989). Mapping Hypertext: Analysis, Linkage, and Display of Knowledge for the Next Generation of On-line Text and Graphics. Lexington, Mass.: Lexington Institute.
Thomas, L. (1981). Debating the unknowable. Atlantic Monthly, July, 49-50.
Toulmin, S. (1958). The Uses of Argument, Cambridge: Cambridge University Press.
Toulmin, S., R. Rieke, & A. Janik. (1979). An Introduction to Reasoning. New York: Macmillan.
Turing, A. (1950). Computing machinery and intelligence. Mind 59, 434-460.
You May Also Like
Comments
Leave a Reply





