ISSA Proceedings 2010 – Powerful Arguments: Logical Argument Mapping

• by: Michael H.G. Hoffmann - Georgia Institute of Technology

1. Introduction
We all know that deductively valid arguments form only a very small subset of all possible arguments. If we would try to provide a complete overview of all forms of arguments people are using in all areas of life, it would hardly be a good idea to focus only on the few well-known argument schemes of propositional and categorical logic. However, the goal of representing all possible argument forms in a complete system of argument representation is not all what argumentation theory is about. Another legitimate part of argumentation theory is to develop argument representation systems for specific purposes.  This has been done, for example, by Perelman & Olbrechts-Tyteca (1969 <1958>) for arguments whose primary purpose is to persuade somebody; by the pragma-dialectical approach for arguments whose primary function is reaching consensus (van Eemeren & Grootendorst 2004); and by the epistemological approach to argumentation for arguments whose “standard function” is to justify knowledge and truth claims (Lumer 2005a, 2005b; Goldman 1999).

In contrast to these approaches to argumentation, I am interested in argument visualization systems whose primary purpose is to stimulate reflection and to confront people with the limits of their own understanding; that is, to stimulate critical reflection on one’s own assumptions, especially those that usually remain hidden. I would like to discuss argument visualization systems that focus on reflection under the heading of “reflective argumentation.” This comes close to the way Tim van Gelder defines “deliberation”: an activity, performed collectively or individually, that is “aimed at determining one’s own attitude” (van Gelder 2003, p. 98; see also van Gelder 2007). The central idea of reflective argumentation can be captured by a nice quote by Andre Maurois that Paul Kirschner, Simon Buckingham Shum, and Chad Carr used as a motto for their seminal book Visualizing Argumentation: Software Tools for Collaborative and Educational Sense-making: “The difficult part in an argument is not to defend one’s opinion but rather to know it” (Kirschner, Buckingham Shum, & Carr 2003, p. vii).

Wesley Salmon wrote already 50 years ago that the deductive argument “is designed to make explicit the content of the premises” (Salmon 1963, p. 15). Exactly this is the reason why I consider deductively valid argument forms as being crucial for reflective argumentation. Based on the fact that we know how deductive arguments like modus ponens or disjunctive syllogism must be constructed, we can take any claim we want to argue for and construct the premises so that they fit into the logical scheme we think is most adequate. This way, we can study those assumptions that would be necessary to guarantee the truth of a conclusion, and we can experiment with alternative formulations of our conclusion and our reasons to improve our argument. Since the chosen argument scheme itself should not be controversial based on its deductive form, we can concentrate our efforts on the question which argument scheme is most appropriate, and how to formulate the content of premises and conclusions. Thus, we are encouraged to focus on what is most important for any argument: the conclusion, the reasons, and the connection between reasons and conclusion.

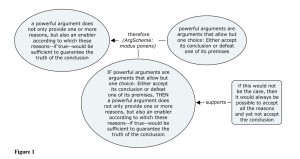
For the purpose of this paper I call arguments that support reflection along these lines “powerful arguments.” More precisely, I define powerful arguments as arguments that leave only one choice for a potential opponent: either to accept the conclusion or to defeat one of its premises. In the first part of this contribution, I will present an argument for the thesis that so defined powerful arguments are possible when we do not only provide reasons as premises of an argument, but also what I call an “enabler.” An “enabler” is that premise in an argument that guarantees that the reason provided in this argument is sufficient to justify the claim or conclusion. In the second part I am providing an argument for the theses that powerful arguments promote mutual understanding and self-reflexivity.

I will present both these arguments by means of Logical Argument Mapping (LAM), a method for the visualization of arguments that I developed over the past years. Compared to other argument visualization tools (see Scheuer, Loll, Pinkwart, & McLaren 2010 for an overview), LAM is unique in requiring that every main argument and every argument that might be controversial in an argumentation has to be constructed by means of a deductively valid argument scheme (see http://lam.spp.gatech.edu/, and for a planned web-based and interactive software version http://agora.gatech.edu/). Since a deductively valid argument is only complete if it includes a conclusion, one or more reasons, and an “enabler” that guarantees that this reason (or these reasons) – if true – are sufficient to determine the truth of the conclusion, LAM promotes the construction of powerful arguments.

In the third part, finally, I will demonstrate with an example how LAM can facilitate a better understanding of others and of our own reasoning. My example is an article by Thomas Nagel in which he argued that we don’t have a moral obligation to respond to the “gruesome facts of inequality in the world economy.”

2. How are powerful arguments possible?
My argument for the thesis that powerful arguments are possible when we do not only provide reasons, but also an enabler that guarantees that these reasons are sufficient to determine the conclusion, is represented in

Figure 1

In Logical Argument Mapping, statements in oval text boxes represent universal statements. “Universal statement” is defined as a proposition that can be falsified by one counterexample. In this sense, laws, rules, and all statements that include “ought,” “should,” or other forms indicating normativity, are universal statements. Any other proposition is treated as a particular statement, including statements about possibilities. The distinction between universal and particular statements is important only with regard to the consequences of different forms of objections: If a premise is defeated, then the conclusion and every chain of arguments that depends on this premise is defeated as well; but if a premise is only questioned or criticized, then the conclusion and everything depending on it is only questioned, but not defeated. While universal statements can easily be defeated by a counterexample to the rule, law, or norm that is represented in form of a universal statement, it depends on an agreement among deliberators whether a counterargument against a particular statement is sufficient to defeat it, even though it is always sufficient to question it and to shift, thus, the burden of proof.

These considerations show that Logical Argument Mapping realizes – at least in a limited sense – what has been described in the literature as defeasible reasoning (Pollock 2008; Prakken & Vreeswijk 2001; Walton 2006). It is a limited form of defeasible reasoning because not the deductive argument schemes are defeasible, but only reasons and enablers. Although this contradicts the widely shared assumption that only non-deductive reasoning is defeasible (as claimed, for example, by Pollock 1995, p. 40 and p. 85, and Prakken 2010, p. 169), I cannot see any reason not to consider LAM as defeasible reasoning. According to the familiar semantics of defeasible, anything is “defeasible” as long as it “can be defeated.” Any deductive argument can be defeated by defeating one of its premises.

It is important for the reflective power of Logical Argument Mapping that it does not make sense to attack the conclusion of a deductive argument without attacking at least one of the premises, that is, either one of the reasons or the enabler. Since in a deductively valid argument the conclusion is necessarily true if all the premises are true, the attention of a potential opponent – and the attention of the constructor of an argument who is concerned with the possibility of opponents – is naturally directed to the premises.

It is of course possible to construct an independent argument with a conclusion that contradicts the conclusion of a given argument. But such an alternative argument – Pollock would call it a “rebutting defeater” (Pollock, 1995, p. 40) – is in itself not sufficient to defeat the original argument. Since such an alternative argument might be based on reasons and inference rules that the proponent of the original does not accept, the case of conflicting arguments only indicates that proponent and opponent “frame” the problem in question differently; that is, they construct arguments that are based on conflicting belief systems. (See Hoffmann, forthcoming, for an example, reconstructed by means of LAM, of how a Palestinian and an Israeli scholar provide conflicting arguments on how to deal with Hamas after its victory in the 2006 elections.) In Logical Argument Mapping, an argument or argumentation (i.e., network of connected arguments) can only be defeated by taking its assumptions seriously, not by providing something else.

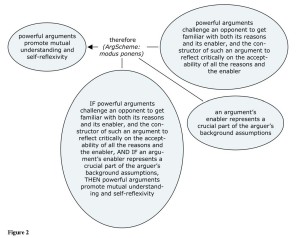
3. Why powerful arguments promote mutual understanding and self-reflexivity
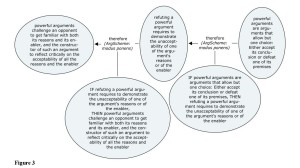
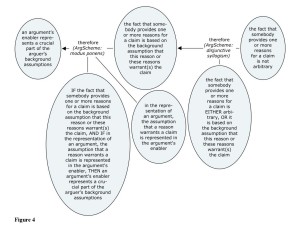
My argument for the thesis that powerful arguments, as long as they are defined as proposed in the introduction, promote mutual understanding and self-reflexivity is, to be precise, an argumentation. That is, the two reasons that are provided in Figure 2 are themselves justified by the arguments represented in Figure 3 and Figure 4.

Figure 2

Figure 3

Figure 4

4. An example: Thomas Nagel’s argument against “global justice”
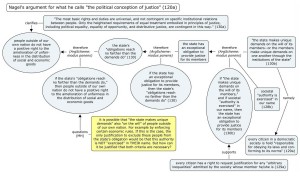
In order to provide a more complex example of how Logical Argument Mapping can be used to support the process of understanding someone’s position, and of our own reasoning about this position, I want to present in Figure 5 a reconstruction of what I think is the core argument of Thomas Nagel’s article “The Problem of Global Justice” (Nagel, 2005). This reconstruction was motivated by the fact that my graduate students found it extremely hard to understand the argument. In my own efforts to identify the structure of Nagel’s argumentation, I went through several revisions of my original LAM map. Each of these revisions led to different objections to his argumentation. The revisions were mainly motivated by attempts to simplify the structure of the argumentation, and to refute my own objections against Nagel’s argument. This way, the experience of revising the argument time and again proves to me the potential of Logical Argument Mapping both to deepen an understanding of the given material and to stimulate self-reflection. I have to say that I found Nagel’s argumentation to be very strong at the end, although I started off with the assumption that his final conclusion is simply unacceptable.

Figure 5 represents only one chain of Nagel’s core argument, and it includes only one objection (in yellow) which “questions” the enabler of the main argument on the left side of the map. The complete core argument consists, I think, of two independent chains of arguments (see http://tinyurl.com/23vweqm).

Figure 5

As can be seen in the online version of the complete core argument, I am inclined to think that the second chain can be defeated. (The online map shows only the defeaters without marking the defeated parts, that is without marking the whole chain of statements that depends on the defeated premises). However, the chain that is represented in Figure 5 still stands, although “questioned” in its final part.

Nagel’s article is 34 pages long. A complete reconstruction of the entire article in a LAM map is published at http://tinyurl.com/22o9q9q. This map consists of about a hundred textboxes.

5. Conclusion
I tried to show in this paper – by means of both an argumentation and an example – that focusing on deductive arguments makes sense when the goal is to stimulate reflection on one’s own reasoning. The notion of “reflective argumentation” can be used to describe this special function of engaging in arguments. The advantage of using deductive arguments for this purpose is that a reconstruction of an argument in logical form can show us how its premises would need to look like if the goal were to guarantee the truth of the conclusion. The point is to get the content of the premises right. This can rather easily be achieved by using the well-known deductive argument schemes as a normative standard of argument construction. This standard determines how the premises must be formulated when we want to argue for a certain claim.

Visualizing arguments and argumentations in deductively valid form stimulates reflection because it challenges the arguer to break down his or her reasoning into argumentative steps as long as it takes to produce a chain of reasons and enablers that are all acceptable for the arguer without further justification. Based on the arguments provided in this paper, I consider Logical Argument Mapping (LAM) to be a powerful form of argument visualization.

REFERENCES
Goldman, A. I. (1999). Knowledge in a Social World. Oxford: Clarendon Press.
Hoffmann, M. H. G. (forthcoming). Analyzing Framing Processes in Conflicts and Communication by Means of Logical Argument Mapping. In W. Donohue, S. Kaufman & R. Rogan (Eds.), Framing in Negotiation: State of the Art. New York, NY: Peter Lang.
Kirschner, P. A., Buckingham Shum, S. J., & Carr, C. S. (Eds.). (2003). Visualizing Argumentation: Software Tools for Collaborative and Educational Sense-making. London: Springer.
Lumer, C. (2005a). The Epistemological Theory of Argument—How and Why? Informal Logic, 25(3), 213-243.
Lumer, C. (2005b). Introduction: The Epistemological Theory of Argumentation—A Map. Informal Logic, 25(3), 189-212.
Nagel, T. (2005). The problem of global justice. Philosophy & Public Affairs, 33(2), 113-147.
Perelman, C., & Olbrechts-Tyteca, L. (1969 <1958>). The new rhetoric. A treatise on argumentation (J. Wilkinson & P. Weaver, Trans.). Notre Dame, Ind.: University of Notre Dame Press.
Pollock, J. (2008). Defeasible Reasoning. In J. E. Adler & L. J. Rips (Eds.), Reasoning: Studies of human inference and its foundations (pp. 451-471). Cambridge ; New York: Cambridge University Press.
Pollock, J. L. (1995). Cognitive carpentry. A blueprint for how to build a person. Cambridge, Mass.: MIT Press.
Prakken, H. (2010). On the Nature of Argument Schemes. In C. Reed & C. W. Tindale (Eds.), Dialectics, Dialogue and Argumentation. An Examination of Douglas Walton’s Theories of Reasoning (pp. 167-185). London: College Publications.
Prakken, H., & Vreeswijk, G. (2001). Logics of defeasible argumentation. In D. M. Gabbay & F. Guenthner (Eds.), Handbook of philosophical logic (2nd ed., Vol. IV, pp. 219-318). Dordrecht; Boston: Kluwer Academic Publishers.
Salmon, W. C. (1963). Logic. Englewood Cliffs, N.J.: Prentice Hall.
Scheuer, O., Loll, F., Pinkwart, N., & McLaren, B. M. (2010). Computer-Supported Argumentation: A Review of the state of the art. International Journal of Computer-Supported Collaborative Learning, 5(1), 43-102.
van Eemeren, F. H., & Grootendorst, R. (2004). A Systematic Theory of Argumentation. The pragma-dialectical approach. Cambridge Cambridge University Press.
van Gelder, T. J. (2003). Enhancing Deliberation Through Computer-Supported Argument Visualization. In P. A. Kirschner, S. J. Buckingham Shum & C. S. Carr (Eds.), Visualizing Argumentation: Software Tools for Collaborative and Educational Sense-making (pp. 97-115). London: Springer.
van Gelder, T. J. (2007). The Rationale for Rationale. Law, Probability & Risk, 6(1-4), 23-42.
Walton, D. (2006). Fundamentals of Critical Argumentation. Cambridge; New York: Cambridge University Press.

You May Also Like

ISSA Proceedings 2006 ~ The Criminal Abduction Paradox

ISSA Proceedings 2006 ~ A Discussion Of Habermas’ Reading And Use Of Toulmin’s Model Of Argumentation

ISSA Proceedings 2006 ~ The Rules Of The Critical Discussion And The Development Of Critical Thinking

ISSA Proceedings 2006 ~ An Analysis Of Preschool Hebrew Speaking Children’s Arguments From The Perspective Of The Pragma-Dialectical Model

ISSA Proceedings 2006 ~ Putin’s Terrorism Discourse As Part of Democracy And Governance Debate In Russia

ISSA Proceedings 2006 ~ Cultural Differences In The Persuasiveness Of Normatively Strong And Normatively Weak Expert Evidence

Comments